
E(k)的这种表示法称为周期布里渊区图象。 扩展布里渊区图象:不同的能带在k空间中不同的布里 渊区中给出; 简约布里渊区图象:所有能带都在简约区中给出: 周期布里渊区图象:在每一个布里渊区中给出所有能带。 2.能带重叠的条件 我们已证明,在布里渊区内部,电子能量是连续的 (严格应为准连续),而在布里渊区边界上,电子能量不 连续,会发生能量的突变。在一维情况下,布里渊区边界 上能量的突变为:△E=E+一E-=2Un 这就是禁带的宽度(能隙)
En (k) 的这种表示法称为周期布里渊区图象。 扩展布里渊区图象:不同的能带在k空间中不同的布里 渊区中给出; 简约布里渊区图象:所有能带都在简约区中给出; 周期布里渊区图象:在每一个布里渊区中给出所有能带。 2. 能带重叠的条件 我们已证明,在布里渊区内部,电子能量是连续的 (严格应为准连续),而在布里渊区边界上,电子能量不 连续,会发生能量的突变。在一维情况下,布里渊区边界 上能量的突变为:DE=E+-E-=2ïUn ï 这就是禁带的宽度(能隙)
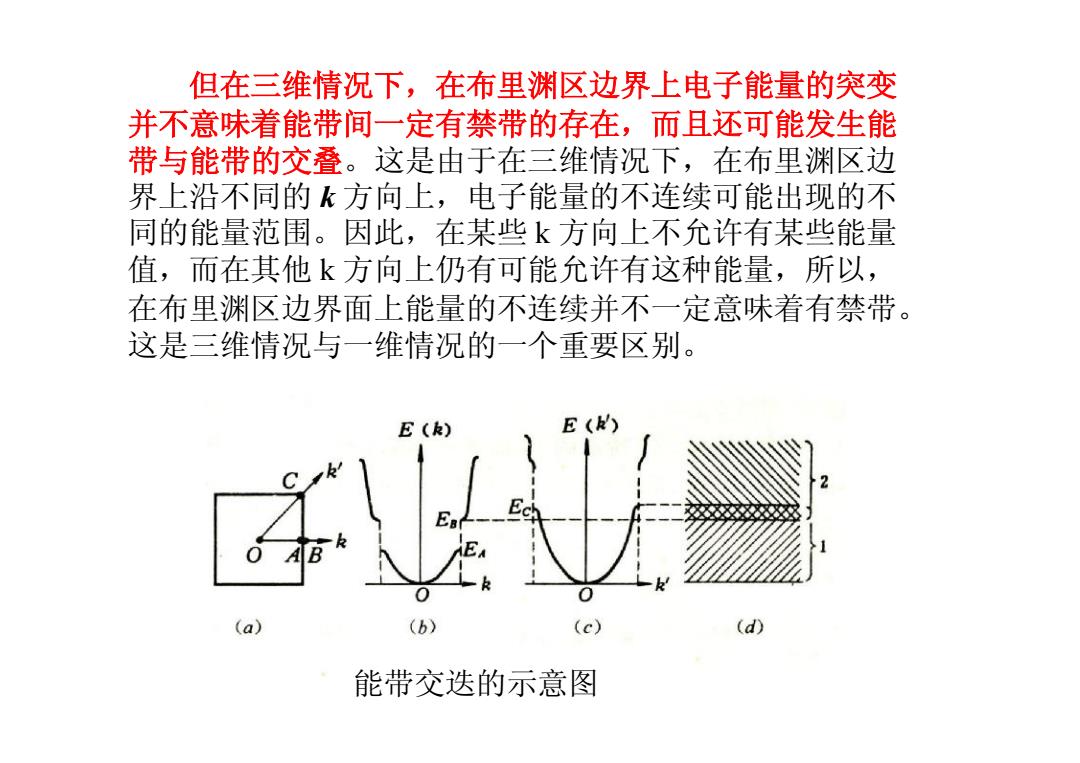
但在三维情况下,在布里渊区边界上电子能量的突变 并不意味着能带间一定有禁带的存在,而且还可能发生能 带与能带的交叠。这是由于在三维情况下,在布里渊区边 界上沿不同的k方向上,电子能量的不连续可能出现的不 同的能量范围。因此,在某些k方向上不允许有某些能量 值,而在其他k方向上仍有可能允许有这种能量,所以, 在布里渊区边界面上能量的不连续并不一定意味着有禁带。 这是三维情况与一维情况的一个重要区别。 E(k) E() (a) (b) (c) (d) 能带交迭的示意图
但在三维情况下,在布里渊区边界上电子能量的突变 并不意味着能带间一定有禁带的存在,而且还可能发生能 带与能带的交叠。这是由于在三维情况下,在布里渊区边 界上沿不同的 k 方向上,电子能量的不连续可能出现的不 同的能量范围。因此,在某些 k 方向上不允许有某些能量 值,而在其他 k 方向上仍有可能允许有这种能量,所以, 在布里渊区边界面上能量的不连续并不一定意味着有禁带。 这是三维情况与一维情况的一个重要区别。 能带交迭的示意图

小结:近自由电子近似的主要结果: 1.存在能带和禁带: 在零级近似下,电子被看成自由粒子,能量本征值E<o,作 为k的函数具有抛物线形式。由于周期势场的微扰,E(k) 函数将在 k=2江n处断开,本征能量发生突变,出现能量 间隔2|V。|,间隔内不存在允许的电子能级,称禁带:其 余区域仍基本保持自由电子时的数值。周期势场的变化愈激 烈,各傅里叶系数也愈大,能量间隔也将更宽,周期势场中 电子的能级形成能带是能带论最基本和最重要的结果
小结:近自由电子近似的主要结果: 1. 存在能带和禁带: 在零级近似下,电子被看成自由粒子,能量本征值 EK (0) 作 为 k 的函数具有抛物线形式。由于周期势场的微扰,E(k) 函数将在 处断开,本征能量发生突变,出现能量 间隔 2︱Vn︱,间隔内不存在允许的电子能级,称禁带;其 余区域仍基本保持自由电子时的数值。周期势场的变化愈激 烈,各傅里叶系数也愈大,能量间隔也将更宽,周期势场中 电子的能级形成能带是能带论最基本和最重要的结果。 k n a 2p =

2.第一(简约)Brilouin区: 自由电子波矢k的取值范围是没有限制的。而在周期势场中,则被严 格的限制在第一Brilouin区内。但从能量角度看,可以将标志电子状态的 波矢k分割为许多区域,在每个区域内电子能级E(k)随波矢k准连续变化 并形成一个能带,波矢k的这样一些区域就被称为Brilouin区,当波矢k 被限制在第一Brilouin区时,E(k)就成为k的多值函数,为了区别,按其 能量由低到高,分别标注为E(K),E2(k)E(K),.。有时也可以用周期布 里渊区图式或扩展布里渊区图式绘出晶体中的能带。 3.解释了导体和绝缘体的区别
2. 第一(简约)Brilouin 区: 自由电子波矢 k 的取值范围是没有限制的。而在周期势场中,则被严 格的限制在第一 Brilouin 区内。但从能量角度看,可以将标志电子状态的 波矢 k 分割为许多区域,在每个区域内电子能级 E(k)随波矢 k 准连续变化 并形成一个能带,波矢 k 的这样一些区域就被称为 Brilouin 区,当波矢 k 被限制在第一Brilouin 区时, E(k) 就成为 k 的多值函数,为了区别,按其 能量由低到高,分别标注为 E1 (k) ,E2 (k) E3 (k), ……。有时也可以用周期布 里渊区图式或扩展布里渊区图式绘出晶体中的能带。 3. 解释了导体和绝缘体的区别