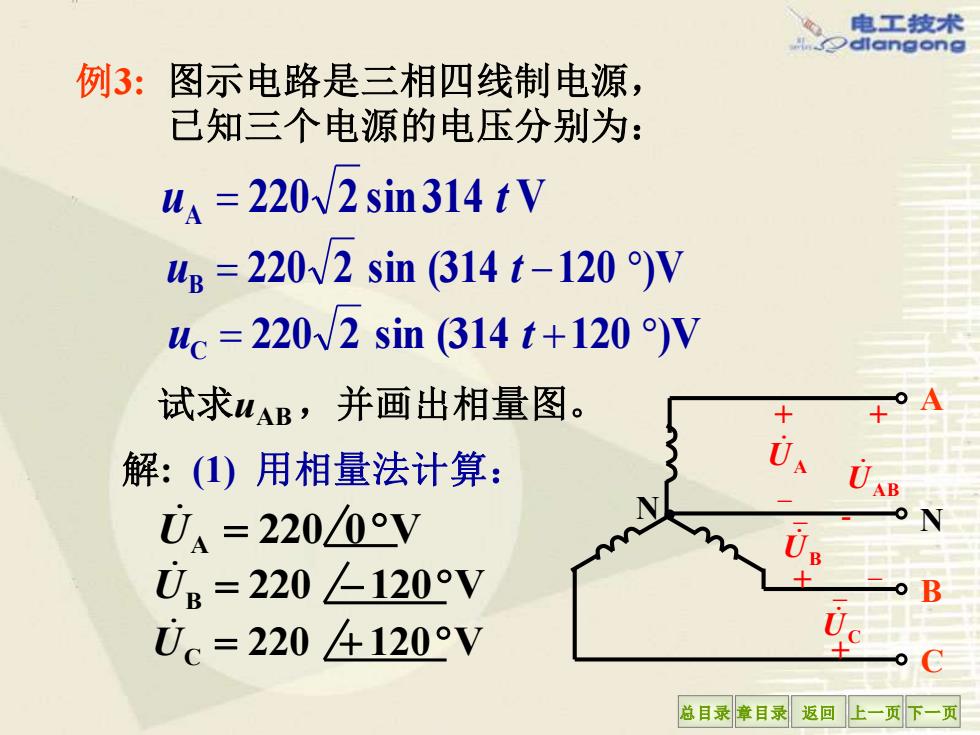
电工技术 dlangong 例3:图示电路是三相四线制电源, 已知三个电源的电压分别为: u=220v2 sin314 tV 4g=220W2sin314t-120)V uc=220W2sin(314t+120)V 试求uAB,并画出相量图。 解:()用相量法计算: 0、 UAB UA=2200°V N 0.=220120V B 0c=2204120V 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 例3: 图示电路是三相四线制电源, 已知三个电源的电压分别为: uB = 220 2 sin (314 t −120 )V uA = 220 2 sin314 t V uC = 220 2 sin (314 t +120 )V 试求uAB ,并画出相量图。 N C A N B + – + + - + UA UB – UC – UAB – 解: (1) 用相量法计算: U A = 220 0V U B = 220 −120V U C = 220 + 120V

电工技术 dlangong 由KVL定律可知 UAB=0A-U.=220V-220∠120V 0AB=220V-220[c0s(-120)+jsin(-120)]N =220(1+0.5+j0.866)V =220×1.7330V =38030V 所以4B=380W2sin(wt+30)V 30 (2)相量图 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 所 以uAB = 380 2 sin(ωt + 30)V (2) 相量图 由KVL定律可知 UA UB UC B -U UAB 30 U AB = U A −U B = 220 0V − 220 −120 V U AB = 220 V − 220 cos (−120 ) + jsin (−120) V = 220 (1+ 0.5 + j0.866 )V = 220 1.73 30V = 380 30V
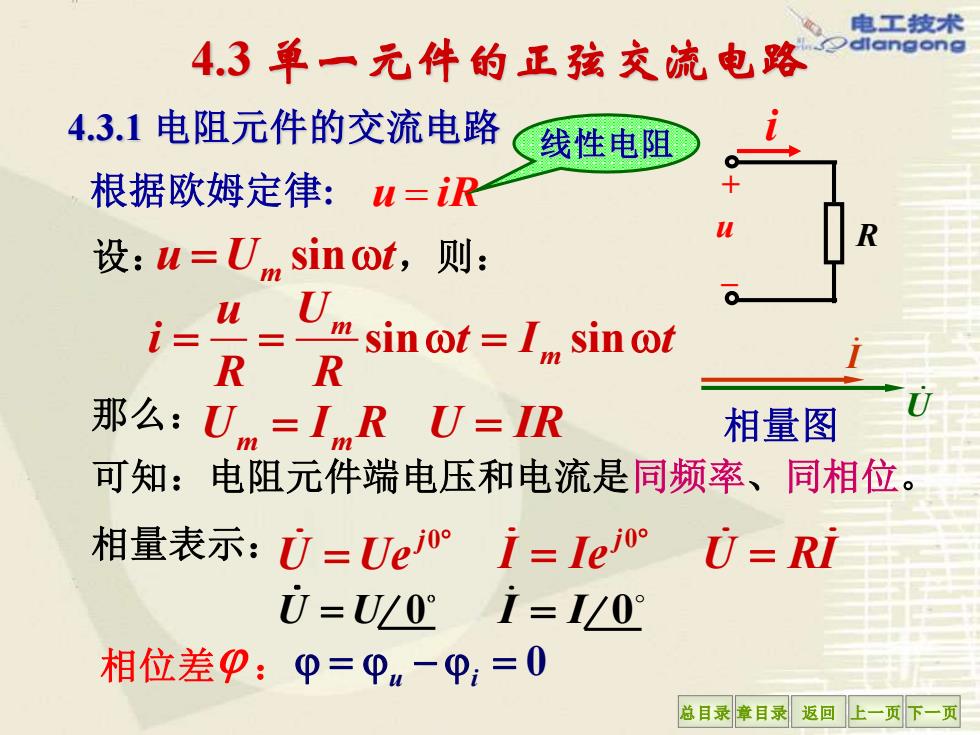
电工技术 4.3单一元件的正孩交流电路 dlangong 4.3.1电阻元件的交流电路 线性电阻 根据欧姆定律:u=R 设:u=U sint,则: U i= m sinot=I sinot R R 那么:U=LRU=I 相量图 m 可知:电阻元件端电压和电流是同频率、同相位。 相量表示:0=Uej0°i=lej U=Ri 0=U/0°i=1/0 相位差9:p=Pn-p:=0 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 4.3.1 电阻元件的交流电路 根据欧姆定律: u = iR 线性电阻 可知:电阻元件端电压和电流是同频率、同相位。 R i u + _ 4.3 单一元件的正弦交流电路 设: u U t = m sin ,则: sin sin m m u U i t I t R R = = = 那么: U I R m m = U IR = 相量表示: j0 U Ue = j0 I Ie = U RI = U U= 0 I = I 0 0 相位差 : = − = u i I U 相量图
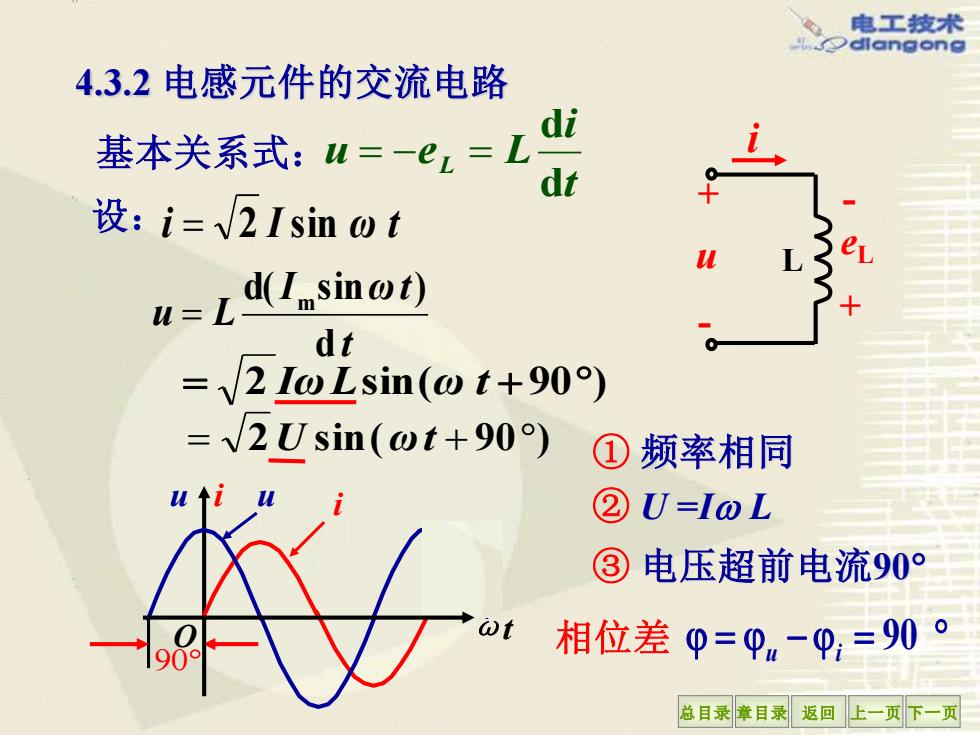
电工技术 dlangong 4.3.2电感元件的交流电路 di 基本关系式:u=-e=L dt 设:i=√2 Isin @t d(Isinot) dt =V2LωLsin(wt+90) =√2Usin(ωt+90) ①频率相同 u↑1 ②U=loL ③电压超前电流90° @t 相位差0=0-0,=0 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 = 2 IωLsin(ω t + 90) 基本关系式: ① 频率相同 ② U =I L ③ 电压超前电流90 90 相位差 = − = u i 4.3.2 电感元件的交流电路 90 t i u eL L d d = − = 设: i = 2 I sin ω t i u + - eL + - L t I ωt u L d d( sin ) m = = 2U sin(ωt + 90) u ωt u i i O

电工技术 dlangong ∫i=V2 Isinot u=IoL:sim (0t+9) 有效值:U=I·wL 或I= @L 定义: X,=oL=2πfL 感抗(⑨) 则: 0=1X, 直流:f=0,X=0,电感L视为短路 X,=2πfL 交流:f↑一Xt 电感L具有通直阻交的作用 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 u = 2I ω Lsin (ωt + 90 ) i = 2I sinωt 或 L U I = XL 则: U = I 感抗(Ω) 电感L具有通直阻交的作用 直流:f = 0, XL =0,电感L视为短路 定义: XL =L = 2 f L XL = 2 π fL 有效值: U = I ω L 交流:f XL