电工技术 dlangong 4.2正孩量的相量表示法 1.正弦量的表示方法 波形图 瞬时值表达式 u=U sin(ot+) 相量 U=U∠φ 必须小写 重点 前两种不便于运算,重点介绍相量表示法。 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 4.2 正弦量的相量表示法 瞬时值表达式 m u U t = + sin( ) 前两种不便于运算,重点介绍相量表示法。 波形图 1. 正弦量的表示方法 重点 相量 U U= 必须小写 u O ω t
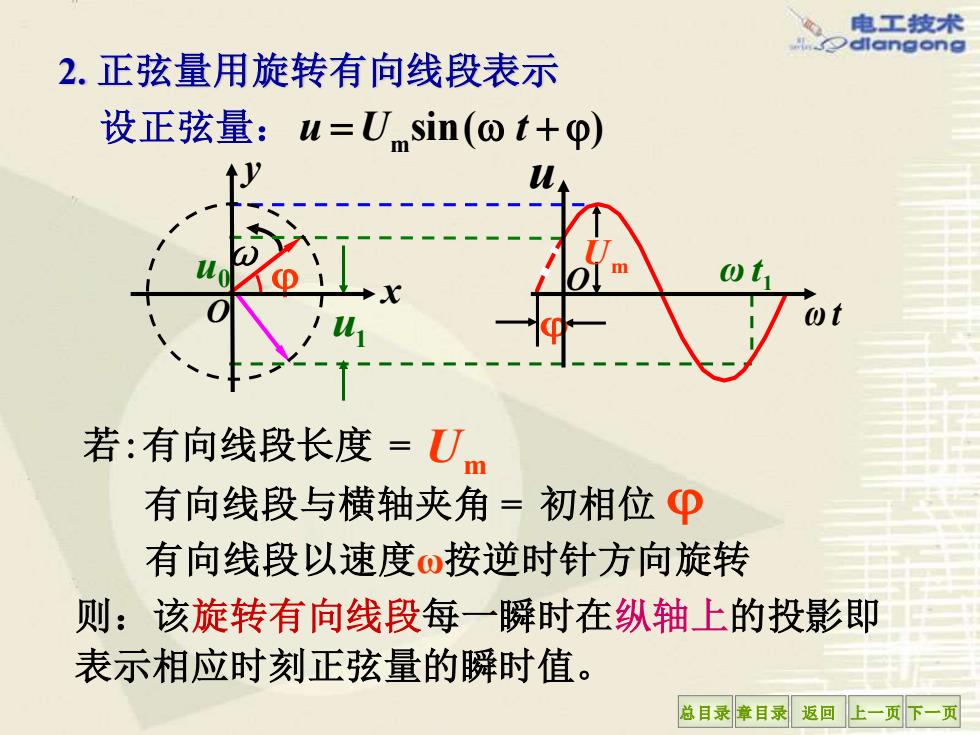
电工技术 dlangong 2.正弦量用旋转有向线段表示 设正弦量:u=U sin(ot+p) 若:有向线段长度=Um 有向线段与横轴夹角=初相位① 有向线段以速度o按逆时针方向旋转 则:该旋转有向线段每一瞬时在纵轴上的投影即 表示相应时刻正弦量的瞬时值。 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 2. 正弦量用旋转有向线段表示 ω m 设正弦量: u U t = + sin( ) 若:有向线段长度 = Um 有向线段以速度ω按逆时针方向旋转 则:该旋转有向线段每一瞬时在纵轴上的投影即 表示相应时刻正弦量的瞬时值。 有向线段与横轴夹角 = 初相位 u1 1 u0 ω t x y O Um u ω t O

电工技术 dlangong 3.正弦量的相量表示 实质:用复数表示正弦量 复数表示形式(设A为复数) ()代数式A=M+jb 式中:a=rc0sp 复数的模 b=rsin o 复数的辐角 (2)三角式 A=rcos o+jrsin=r(cos +jsin 由欧拉公式: epte-i9 ejo-e-io C0S0= sin 2 2i 可得:e9=cosp+jsino 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 +j +1 b A a r 0 3. 正弦量的相量表示 复数表示形式(设A为复数) (1) 代数式 A =a + jb arctan b a = 2 2 r = a + b 复数的模 复数的辐角 实质:用复数表示正弦量 式中: a r = cos b r = sin (2) 三角式 A r r r = + = + cos j sin (cos jsin ) 由欧拉公式: j j e e sin 2j − − = j j e e cos , 2 − + = j e cos jsin 可得: = +

电工技术 (3)指数式 A=reio dlangong ④)极坐标式A=/迎 A=a+jb=rcoso+jrsin=re=r/o 相量:表示正弦量的复数称相量 设正弦量:u=Usin(ot+p) 电压的有效值相量 相量表示: U=Vei=UL 相量的模=正弦量的有效值 相量辐角=正弦量的初相角 U=Ue=Ulo 相量的模=正弦量的最大值 m 相量辐角=正弦量的初相角 电压的幅值相量 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 (3) 指数式 j A r e = m 设正弦量: u U= + sin( ) ωt 相量: 表示正弦量的复数称相量 电压的有效值相量 j A a b r j r r r j cos sin e = + = + = = (4) 极坐标式 A r = 相量表示: 相量的模=正弦量的有效值 相量辐角=正弦量的初相角 j U Ue U = = 相量的模=正弦量的最大值 相量辐角=正弦量的初相角 j U U e U m m m = = 电压的幅值相量

电工技术 注意: dlangong ①相量只是表示正弦量,而不等于正弦量。 i=Isin(ot+)=Imp ②只有正弦量才能用相量表示, 非正弦量不能用相量表示。 ③相量的两种表示形式 相量式:U=Ue=以p=U(cosp+jsin) 相量图:把相量表示为复平面上的有向线段图形 可不画坐标轴 总目录章目录返回上一页下一页
总目录 章目录 返回 上一页 下一页 ① 相量只是表示正弦量,而不等于正弦量。 注意: m i I = + sin( ) ωt ② 只有正弦量才能用相量表示, 非正弦量不能用相量表示。 j m m I e I ? = = = ③ 相量的两种表示形式 相量图: 把相量表示为复平面上的有向线段图形 可不画坐标轴 j U U U U e (cos jsin ) 相量式: = = = + I U