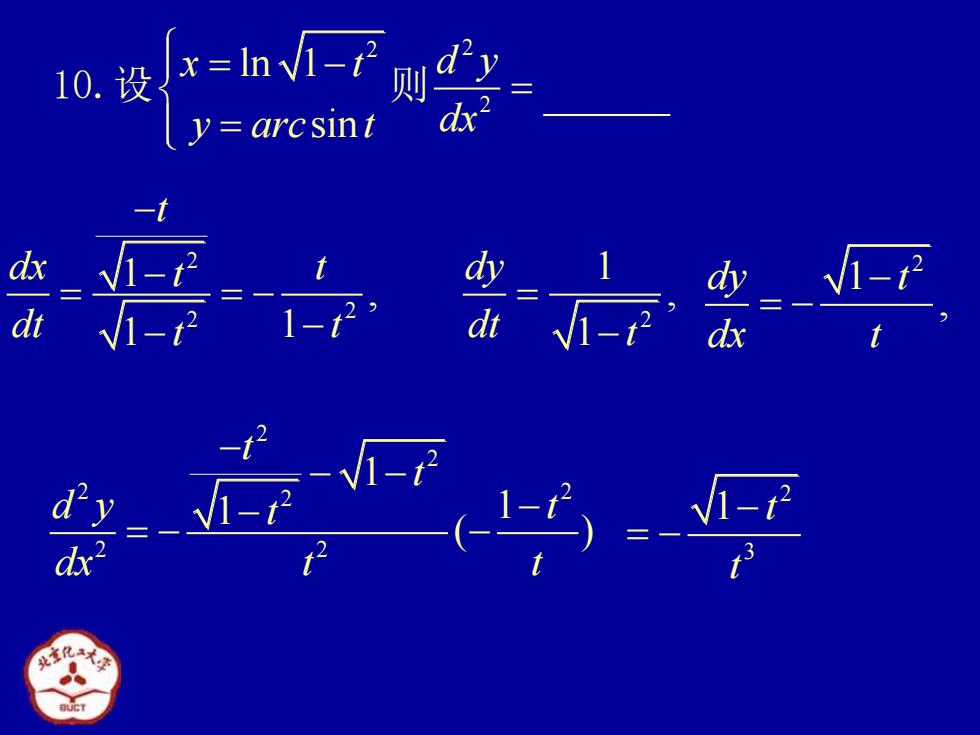
dx d 2
2 3 1 t t − = − 2 2 2 ln 1 sin x t d y y arc t dx = − = = 10.设 则 2 2 2 2 1 1 , , 1 1 1 t dx t dy t dt t dt t t − − = = − = − − − 2 2 2 2 2 2 2 1 1 1 ( ) t t d y t t dx t t − − − − − = − − 2 1 , dy t dx t − = −

1.设断)=如xa=,则= du -西.-道.1 xsec2x-tanx 1 du dx du dx du x2 2x dx xsec-x-tan x 2x3 12.极限1 msinx·arctan上=0 x→0 X 有界变量与无穷小的乘积为无穷小
2 tan ( ) , x df f x u x x du 11.设 = = ,则 = df df dx df 1 du dx du dx du dx = = 0 1 limsin arctan x x → x 12.极限 = 有界变量与无穷小的乘积为无穷小 2 2 sec tan 1 2 x x x x x − = 2 3 sec tan 2 x x x x − = 0
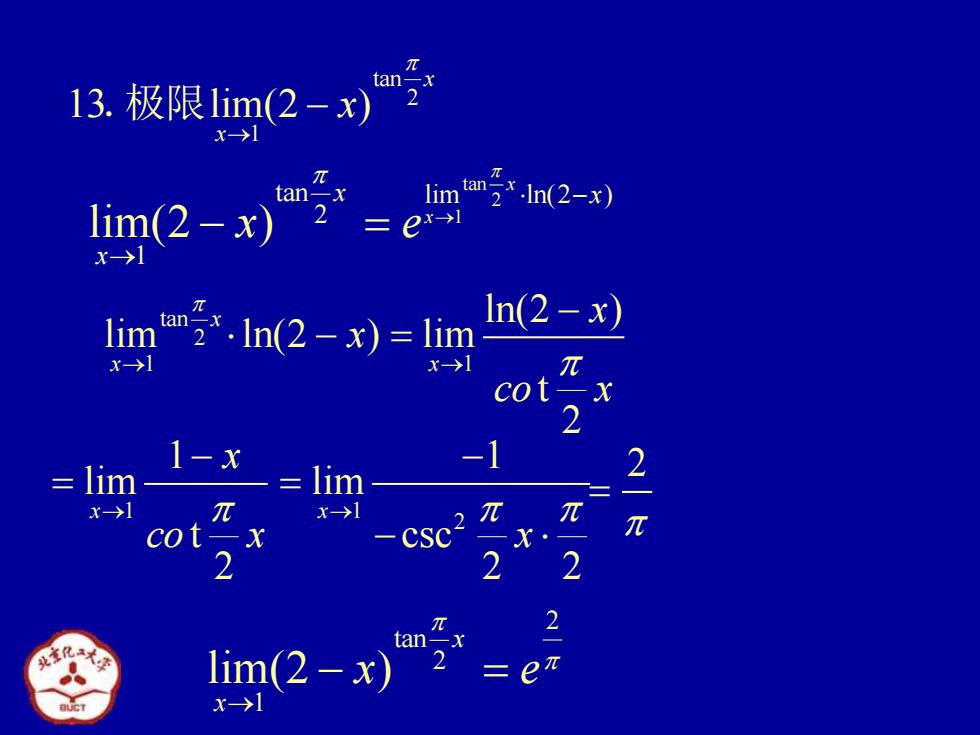
π 13.极限1im(2-x) x→1 π tan X 2-x) limtan2*.In(2-x) 2”=e limm吃x-ln(2-x)=lim n(2-x) x>1 x→1 π cotx 2 1-x -1 lim lim x-→1 x>] 2 cot-x 一X· π 2 π 2 tan lim(2-x) 2 =eπ x→1
tan 2 1 13 lim(2 ) x x x → .极限 − tan 2 1 tan lim ln(2 ) 2 1 lim(2 ) x x x x x x e → − → − = tan 2 1 1 ln(2 ) lim ln(2 ) lim t 2 x x x x x co x → → − − = 1 1 2 1 1 lim lim t csc 2 2 2 x x x co x x → → − − = = − 2 = 2 tan 2 1 lim(2 ) x x x e → − =

14.极限1im 0+x2-1 x→0 1-cosx lim 1+x2-1 1x2 lim n 2 x→0 1-cosx →0 n 2 15.极限lim x-sinx *In(1+x).tanx x-sInx lim x-sInx 1-cosx lim =lim x In(1+x).tanx x-→0 x.x2 x→0 3x2 sin x lim x>0 6x 6
1 2 0 (1 ) 1 14 lim 1 cos n x x → x + − = − .极限 1 2 2 0 0 2 1 (1 ) 1 lim lim 1 cos 1 2 n x x x x n x x → → + − = − 2 n = 2 0 sin 15 lim x ln(1 ) tan x x → x x − = + .极限 2 2 0 0 sin sin lim lim x x ln(1 ) tan x x x x → → x x x x − − = + 2 0 1 cos lim x 3 x → x − = 0 sin 1 lim x 6 6 x → x = =