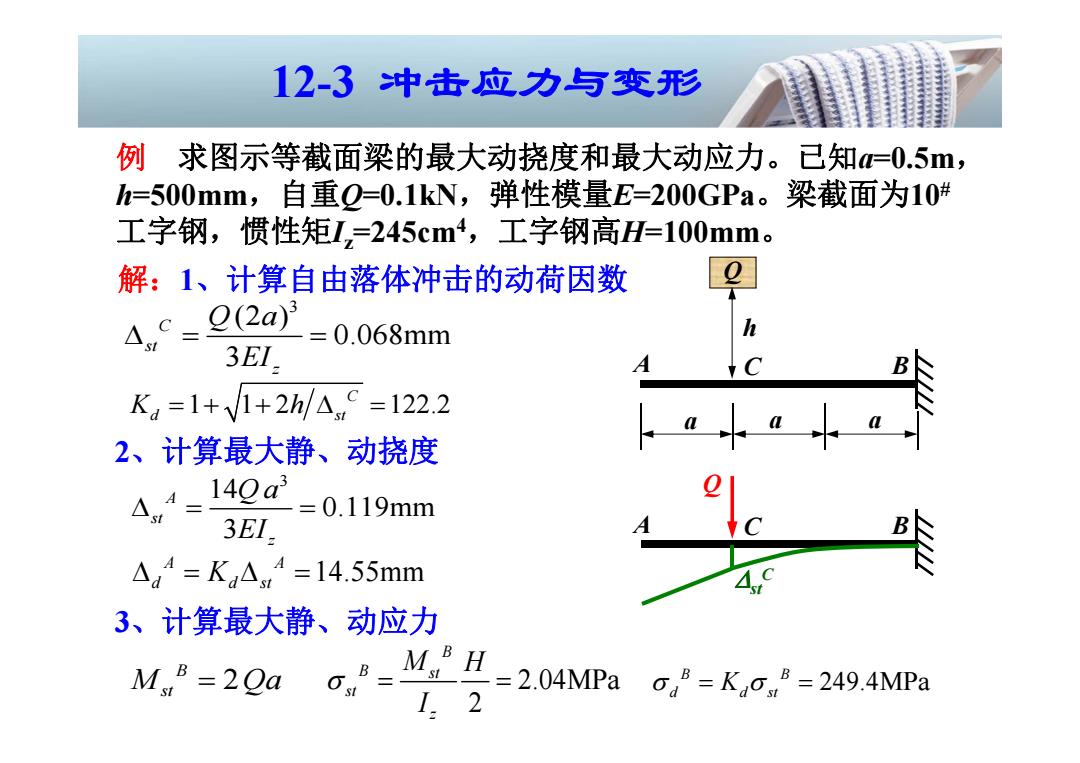
12-3冲击应力与变形 例求图示等截面梁的最大动挠度和最大动应力。己知=0.5m, h=500mm,自重Q=0.1kN,弹性模量E=200GPa。梁截面为10# 工字钢,惯性矩I=245cm4,工字钢高H=100mm。 解:1、计算自由落体冲击的动荷因数 4,-22a'=0.068mm 3EI. A Kg=1+V1+2h/△C=122.2 2、计算最大静、动挠度 4n+=140a3 =0.119mm 3EI. A=KA=14.55mm 3、计算最大静、动应力 M,=20ao,=MH =2.04MPa 3=KGB=249.4MPa I.2
例 求图示等截面梁的最大动挠度和最大动应力。已知a=0.5m, h=500mm,自重Q=0.1kN,弹性模量E=200GPa。梁截面为10# 工字钢,惯性矩Iz=245cm4,工字钢高H=100mm。 解:1、计算自由落体冲击的动荷因数 3 (2 ) 0.068mm 3 C st z Q a EI 1 1 2 122.2 C K h d st 3 14 0.119mm 3 A st z Q a EI 14.55mm A A d d st K 2.04MPa 2 B B st st z M H I 249.4MPa B B d d st K 12-3 冲击应力与变形 Q h A C B a a a Q A C B stC 2、计算最大静、动挠度 3、计算最大静、动应力 2 B Mst Qa
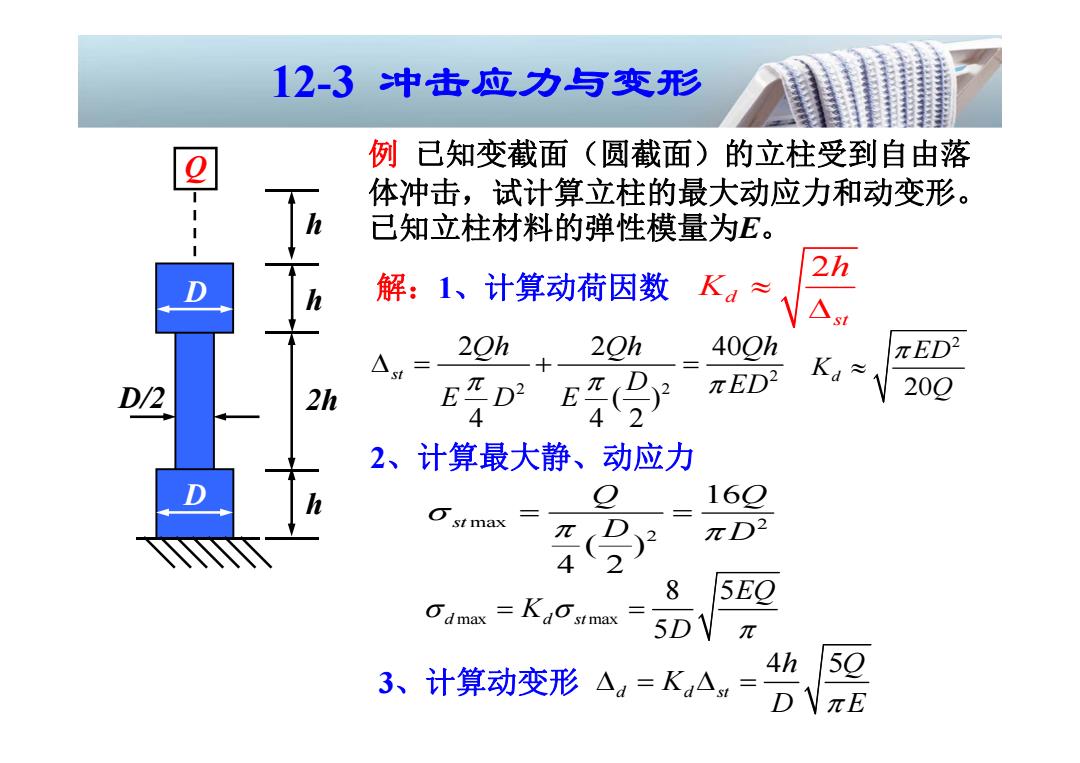
12-3冲击应力与变形 例已知变截面(圆截面)的立柱受到自由落 体冲击,试计算立柱的最大动应力和动变形。 已知立柱材料的弹性模量为E。 2h h 解:1、计算动荷因数K。≈ △st 20h 20h 40Qh πED2 △t= 2h πED2 Ka≈ 20Q 2、计算最大静、动应力 16○ stmax π 12 πD2 8 =Kao'srmax 5EO 5DV 3、计算动变形A=KA= h 59 D NπE
例 已知变截面(圆截面)的立柱受到自由落 体冲击,试计算立柱的最大动应力和动变形。 已知立柱材料的弹性模量为E。 解:1、计算动荷因数 max 2 2 16 ( ) 4 2 st Q Q D D 2 d st h K 2 2 2 2 2 40 ( ) 4 42 st Qh Qh Qh D ED ED E 2 20 d ED K Q max max 8 5 5 d d st EQ K D 12-3 冲击应力与变形 h h 2h h Q D D D/2 2、计算最大静、动应力 3、计算动变形 4 5 d d st h Q K D E

12-4 提高构件动强度的措施 具体措施: ◆减小冲击高度或互相接触构件之间的间隙; ◆ 在保证静强度的前提下,尽量采用弹性模量较 小的材料,或者可能时加软垫、弹簧等; ◆在不降低静强度的前提下,尽量增大静变形; ◆避免采用脆性材料; ◆冲击对应力集中很敏感,应避免采用有凹槽、 缺口、截面突变的构件
12-4 提高构件动强度的措施 减小冲击高度或互相接触构件之间的间隙; 在保证静强度的前提下,尽量采用弹性模量较 小的材料,或者可能时加软垫、弹簧等; 在不降低静强度的前提下,尽量增大静变形; 避免采用脆性材料; 冲击对应力集中很敏感,应避免采用有凹槽、 缺口、截面突变的构件。 具体措施:

第十二章的基本要求 1.明确动载荷的概念,了解动载荷问题的求解思路; 2.掌握自由落体冲击和水平冲击时动荷因数的计算; 3.了解提高构件承受冲击能力的途径
第十二章的基本要求 1.明确动载荷的概念,了解动载荷问题的求解思路; 2.掌握自由落体冲击和水平冲击时动荷因数的计算; 3.了解提高构件承受冲击能力的途径

第十三章疲劳强度 疲劳破坏的概念 口交变应力及其循环特征 ▣材料的疲劳极限 ▣ 对称循环下构件的疲劳极限 ▣非对称循环下构件的疲劳极限 ▣构件的疲劳强度条件 *构件的疲劳寿命估算简介 ▣ 提高构件疲劳强度的措施 西步充通大睾 航天航空学院一力学中心 XIAN JIAOTONG UNIVERSITY
第十三章 疲劳强度 疲劳破坏的概念 交变应力及其循环特征 材料的疲劳极限 对称循环下构件的疲劳极限 非对称循环下构件的疲劳极限 构件的疲劳强度条件 *构件的疲劳寿命估算简介 提高构件疲劳强度的措施 航天航空学院--力学中心