初相位(角)少, i(t)=I sin(@t+w;) 主值范围内取值 w≤180° wt 1 (ot+W)称为正弦量的相位,或称相角。 ,是正弦量在=0时刻的相位,称为正弦量 的初相位(角),简称初相
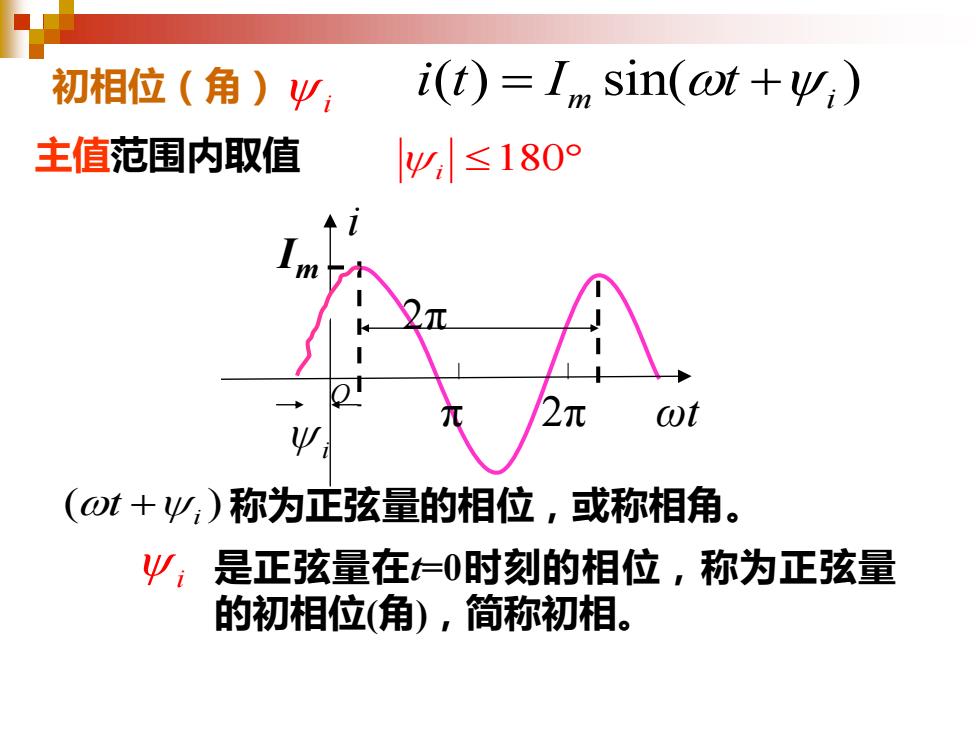
初相位(角) i 主值范围内取值 180 i i Im 2π ωt i O π 2π ( ) i t + 称为正弦量的相位,或称相角。 i 是正弦量在t=0时刻的相位,称为正弦量 的初相位(角),简称初相。 ( ) sin( ) m i i t I t = +

【例6-1-1】i 知右图元件通过的正弦电流 的m=10mA,f=1Hz,初相y马rad。 0 试写出该电流的函数表达式,并求出当t=0.5s和 t=1.25s时电流瞬时值的大小及实际方向。 解w=2π子2πrad/s i=10sin(2πt+空 )mA 当t=0.5s时 i=10sm(2πx0.5+F)mA=-7.07mA 为负值,表示电流的实际方向与参考方向相反。 当t=1.25s时 i=10sin(2π×1.25+ 4)mA=7.07mA 为正值,表示电流的实际方向与参考方向相同
试写出该电流的函数表达式,并求出当t=0.5s 和 t=1.25s时电流瞬时值的大小及实际方向。 解 ω=2πf=2πrad/s i=10sin(2πt + )mA 当t=0.5s时 i=10sin(2π×0.5 + )mA=-7.07mA i为负值,表示电流的实际方向与参考方向相反。 当t=1.25s时 i=10sin(2π×1.25 + )mA=7.07mA i为正值,表示电流的实际方向与参考方向相同。 【例6-1-1】 已知右图元件通过的正弦电流 的Im =10mA,f =1Hz,初相ψ = rad

二、相位差 两个同频率正弦量的相位之差称为相位差,用印表示 习惯上规定p≤180°。 设u=U sin(ot什yu) i=Imsin(wt什4:)) 则它们的相位差为 初相位之差 p=(ωt+4u)-(0t+4》=ΨaΨ ◆两个同频率正弦量的相位差等于它们的初相位之差, 是不随时间而改变的常量, ◆在比较两个正弦量的相位差时,必须:两者的频 率相同,函数形式相同,函数前面的符号都为正或 都为负,初相位的单位相同。否则不能比较
二、相位差 设 u= Umsin(ωt+ψu ) i= Imsin(ωt+ψi ) 则它们的相位差为 j =(ωt +ψu)-(ωt +ψi)=ψu-ψi ◆两个同频率正弦量的相位差等于它们的初相位之差, 是不随时间而改变的常量. ◆在比较两个正弦量的相位差时,必须:两者的频 率相同,函数形式相同,函数前面的符号都为正或 都为负,初相位的单位相同。否则不能比较。 两个同频率正弦量的相位之差称为相位差,用j 表示, 习惯上规定|j |≤180°。 初相位之差
两个同频率正弦量的相位关系 u比i i比u 先到 u,i 先到 达最 达最 大值 大值 (a)u超前i (b) u滞后i 在图(a)中,p=y.4:>0,则称u超前于i(或者说i 滞后于w),其意义是比先到达最大值(或零值。 在图(b)中,p=4:<0,则称滞后于i或者说i 超前于W)
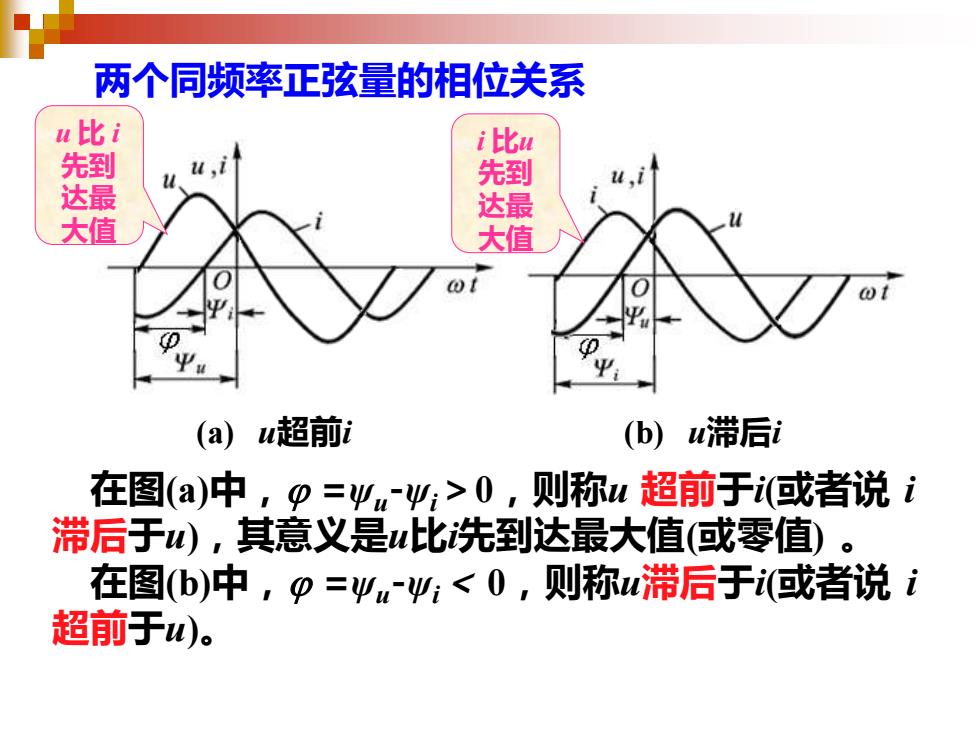
两个同频率正弦量的相位关系 (a) u超前i 在图(a)中,j =ψu-ψi>0,则称u 超前于i(或者说 i 滞后于u),其意义是u比i先到达最大值(或零值) 。 在图(b)中,j =ψu-ψi< 0,则称u滞后于i(或者说 i 超前于u)。 (b) u滞后i u 比 i 先到 达最 大值 i 比u 先到 达最 大值
两个同频率正弦量的特殊相位关系 t.I u,i u,i (a) (b) (a)同相,相位差p0, (b)反相,相位差p=180°, (c)正交,相位差p=90°
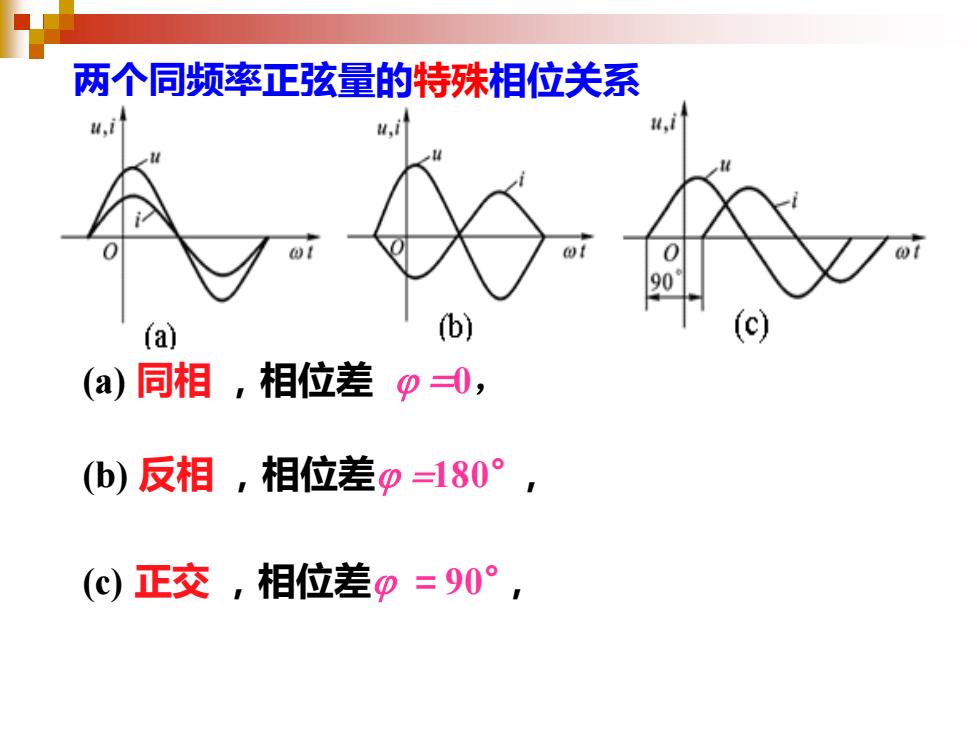
两个同频率正弦量的特殊相位关系 (a) 同相 ,相位差 j =0, (b) 反相 ,相位差j =180° , (c) 正交 ,相位差j =90°