
§6-1正弦量的特征 ◆正弦信号是一种基本信号,任何非正弦周期信号可 以分解为按正弦规律变化的分量。 ◆不论在实际应用中还是在理论分析中,正弦稳态分 析都是十分重要的
§6-1 正弦量的特征 ◆正弦信号是一种基本信号,任何非正弦周期信号可 以分解为按正弦规律变化的分量。 ◆不论在实际应用中还是在理论分析中,正弦稳态分 析都是十分重要的
正弦量的三要素 对应于 1、正弦量 i=I sin ot 随时间按正弦规律变化的电压、 的波形 电流等物理量统称为正弦量。 正弦量的表示方法: (a ()正弦波,即波形图,便于用示波器观察。 对应于 (2)函数式,称为正弦量的瞬时值表 i=Isin(@t+i 的波形 达式。也可以采用余弦函数形式,本 课程采用正弦函数。 i=I sin @t 对应于图(a (b) i=Isin(at+wi) 对应于图(b)
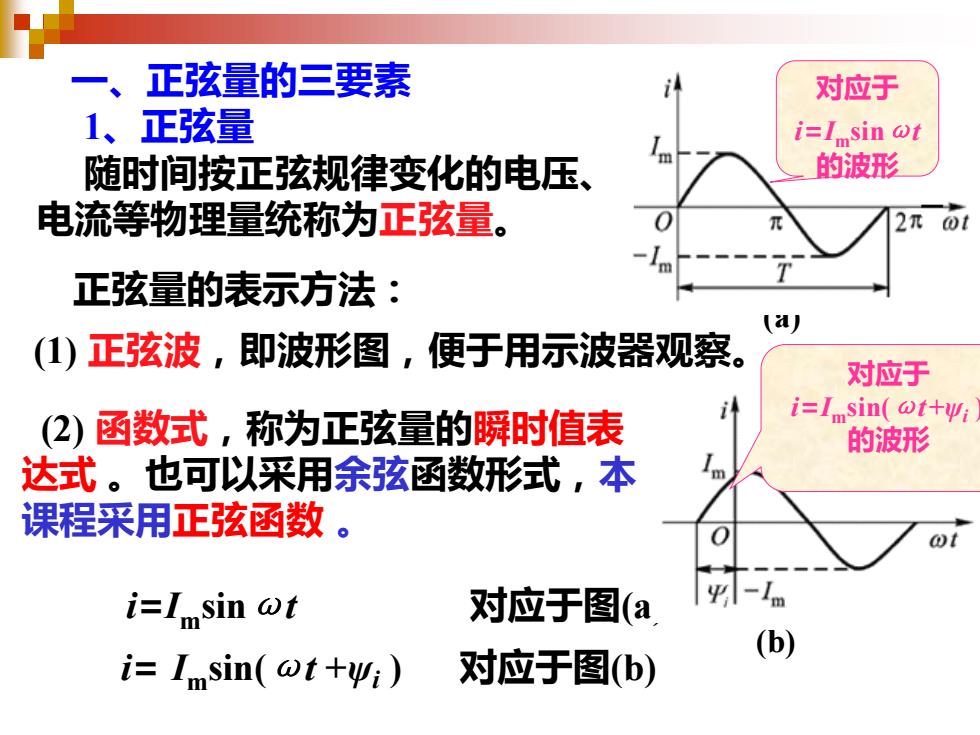
一、正弦量的三要素 1、正弦量 (1) 正弦波,即波形图,便于用示波器观察。 随时间按正弦规律变化的电压、 电流等物理量统称为正弦量。 正弦量的表示方法: (2) 函数式,称为正弦量的瞬时值表 达式 。也可以采用余弦函数形式,本 课程采用正弦函数 。 i=Imsinωt 对应于图(a) i= Imsin(ωt +ψi ) 对应于图(b) (a) (b) 对应于 i=Imsinωt 的波形 对应于 i=Imsin(ωt +ψi ) 的波形

2、正弦量的三要素 i=Isin(@t+wi) (1)幅值(振幅、最大值、峰值) Im是幅值。 (2)周期T、频率f、角频率ω 都是用来表示正弦量变化快慢的参数。 ω=d(ωt什y)/dt:单位时间内变化的角度,单位:rad/s 频率f:每秒钟完成循环的次数,单位为赫兹(Hz) 周期T:完成一个循环变化所需的时间,单位为秒(s) ω=d(wt+w)/dt 0=2mf=2%
(1) 幅值 (振幅、最大值、峰值) 2、正弦量的三要素 i=Imsin(ωt +ψi ) Im是幅值。 (2) 周期T、频率f、角频率ω 都是用来表示正弦量变化快慢的参数。 T f 2π = 2π = T f 2π = 2π = T f 1 ω = =d(ωt+ )/dt ω =d(ωt+ )/dt:单位时间内变化的角度,单位:rad/s 频率f :每秒钟完成循环的次数,单位为赫兹(Hz) 周期T :完成一个循环变化所需的时间,单位为秒(s)

[例]我国和大多数国家的电力标准频率是 50Hz,试求其周期和角频率。 [解] 0.02s w=2πf=2×3.14×50rad/s=314rad/s *电网频率:我国50Hz,美国、日本60Hz * 收音机中频段频率:530~1600kHz *移动通信频率:900MHz1800MHz *无线通信频率:高达300GHz
[例]我国和大多数国家的电力标准频率是 50 Hz,试求其周期和角频率。 [解] 1 T 0.02 s f = = = 2f = 2 3.14 50 rad/s = 314 rad/s * 无线通信频率: 高达 300GHz * 电网频率:我国 50 Hz ,美国 、日本 60 Hz * 收音机中频段频率:530~1600 kHz * 移动通信频率:900MHz~1800 MHz
i=Imsin(wt什y:) (3)相位角(相位)、初相位(初相) 是初相 相位反映了正弦量变化的进程,如电流表达式中的 (ωt+W:)是相位;单位是弧度(rad或度 初相是=0时的相位, |w≤180 初相的大小与所选取的计时“ 初相的大 起点有关。如右图u1的波形 小与所选 取的计时 其初相4=70°。若计时起点 起点有关 在虚线轴,则y=0° 70 初相是正弦波的正半波的起始点到计 时起点(坐标原点)的相位角
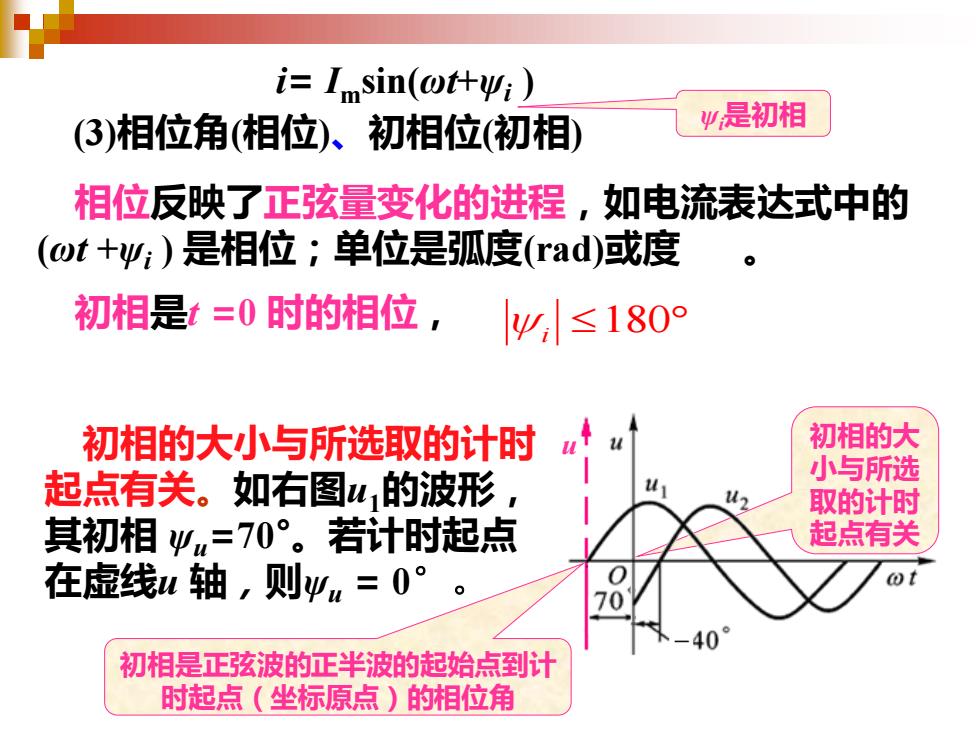
i= Imsin(ωt+ψi ) (3)相位角(相位)、初相位(初相) 相位反映了正弦量变化的进程,如电流表达式中的 (ωt +ψi ) 是相位;单位是弧度(rad)或度 。 初相是t =0 时的相位, 初相的大小与所选取的计时 起点有关。如右图u1的波形, 其初相 ψu =70°。若计时起点 在虚线u 轴,则ψu = 0° 。 u 初相的大 小与所选 取的计时 起点有关 ψi是初相 初相是正弦波的正半波的起始点到计 时起点(坐标原点)的相位角 180 i