
LP Relaxation Rounding Modeling:Express the optimization problem as an Integer Linear Program (ILP). Relaxation:Relax the ILP to a Linear Program (LP). ● Solving:Find the optimal fractional solution by an efficient LP solver. Rounding:Round the optimal fractional solution to a feasible integral solution. Analysis:Prove that the rounded solution is not too far away from the optimal integral solution (usually by comparing with the fractional optimal solution)
• Modeling: Express the optimization problem as an Integer Linear Program (ILP). • Relaxation: Relax the ILP to a Linear Program (LP). • Solving: Find the optimal fractional solution by an efficient LP solver. • Rounding: Round the optimal fractional solution to a feasible integral solution. • Analysis: Prove that the rounded solution is not too far away from the optimal integral solution (usually by comparing with the fractional optimal solution). LP Relaxation & Rounding
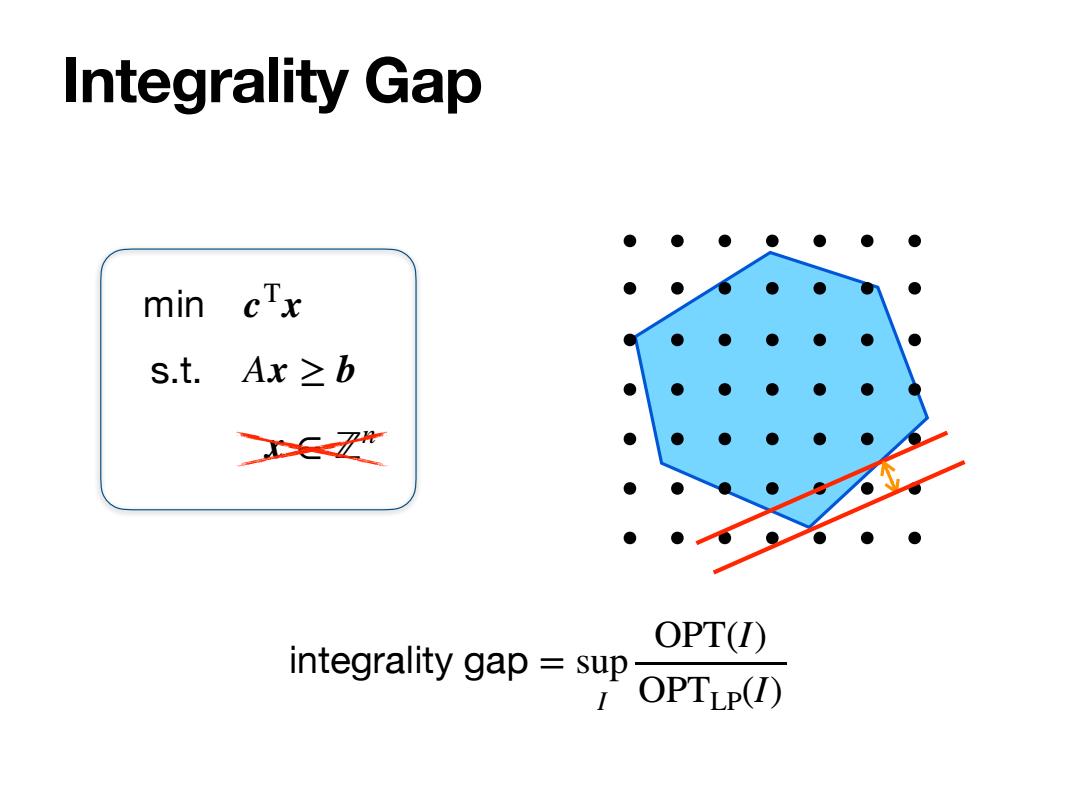
Integrality Gap min 1 cTx s.t.Ax≥b Z OPT() integrality gap sup OPTLPU)
x ∈ ℤn Integrality Gap min s.t. cTx Ax ≥ b integrality gap = sup I OPT(I) OPTLP(I)
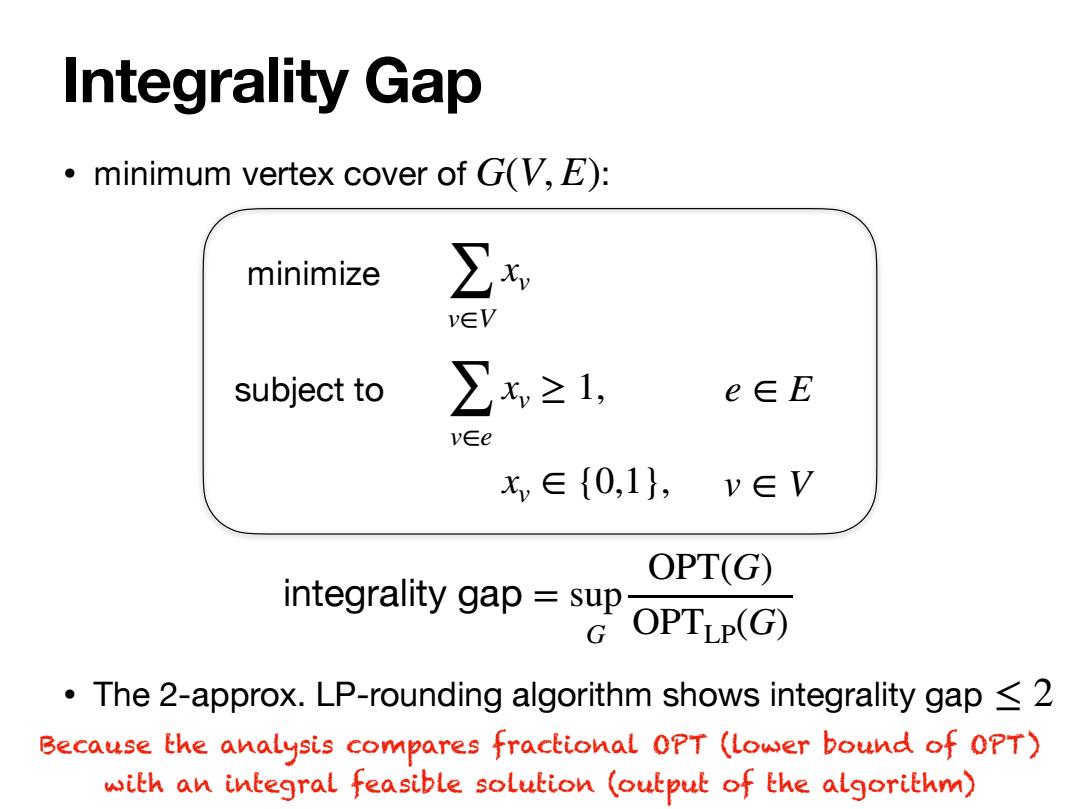
Integrality Gap minimum vertex cover of G(V,E): minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x∈{0,1, v∈V integrality gap OPTG) OPTLP(G) The 2-approx.LP-rounding algorithm shows integrality gap 2 Because the analysis compares fractional OPT (Lower bound of OPT) with an integral feasible solution (output of the algorithm)
• minimum vertex cover of G(V, E): Integrality Gap minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V integrality gap = sup G OPT(G) OPTLP(G) • The 2-approx. LP-rounding algorithm shows integrality gap ≤ 2 Because the analysis compares fractional OPT (lower bound of OPT) with an integral feasible solution (output of the algorithm)
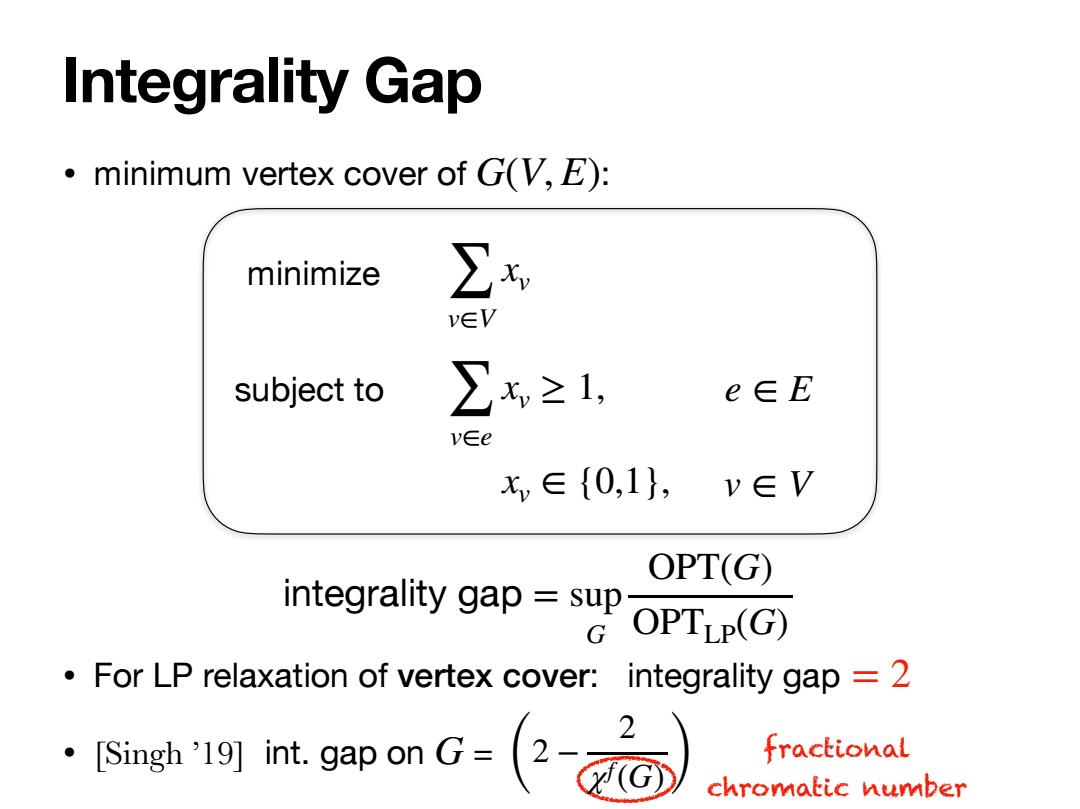
Integrality Gap minimum vertex cover of G(V,E): minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x∈{0,1,v∈V OPT(G) integralitygp OPTLP(G) For LP relaxation of vertex cover:integrality gap =2 .se19 int.=(2δ 2 fractional chromatic number
• minimum vertex cover of G(V, E): Integrality Gap minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V integrality gap = sup G OPT(G) OPTLP(G) • For LP relaxation of vertex cover: integrality gap • [Singh ’19] int. gap on = = 2 G (2 − 2 χf(G)) fractional chromatic number

MAX-SAT
MAX-SAT