
Linear Programming (LP) Canonical form: Standard form: min cTx min cTx s.t.Ax≥b s.t.Ax=b x≥0 x≥0 ax+s;=bi S:≥0 slack variable
Linear Programming (LP) Canonical form: aT i x ≤ bi ⟹ { aT i x + si = bi si ≥ 0 ⟹ min s.t. cTx Ax ≥ b x ≥ 0 min s.t. cTx Ax = b x ≥ 0 Standard form: slack variable

Linear Programming (LP)Solvers min cTx A∈QmXn s.t.Ax=b b∈Qmc∈Q” x≥0 m≤n Dantzig's simplex method Dantzig'47]: walks over polytope vertices along polytope edges exponential time in the worst case(Klee-Minty cube,1972) poly-time in smoothed complexity [Spielman-Teng'01] Solvable in(weakly)polynomial time: ellipsoid method [Khachiyan'80]in O(n)time interior-point methods [Karmarkar84]in O(n2.5)time Vaidya'89]and recently,in current matrix multiplication time [Cohen,Lee,Song'19][Jiang,Song,Weinstein,Zhang'21]
Linear Programming (LP) Solvers min s.t. cTx Ax = b x ≥ 0 • Dantzig’s simplex method [Dantzig ’47]: • walks over polytope vertices along polytope edges • exponential time in the worst case (Klee–Minty cube, 1972) • poly-time in smoothed complexity [Spielman-Teng’01] • Solvable in (weakly) polynomial time: • ellipsoid method [Khachiyan ’80] in time • interior-point methods [Karmarkar ’84] in time [Vaidya ’89] and recently, in current matrix multiplication time [Cohen, Lee, Song ’19] [Jiang, Song, Weinstein, Zhang ’21] O(n6 ) O(n2.5) A ∈ ℚm×n m ≤ n b ∈ ℚm c ∈ ℚn

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest CC Vthat intersects all edges. Integer Linear Program(ILP)for vertex cover: minimize Σx v∈V subject to ∑x≥1, e∈E v∈e x,∈{0,1}, v∈V
• Integer Linear Program (ILP) for vertex cover: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V
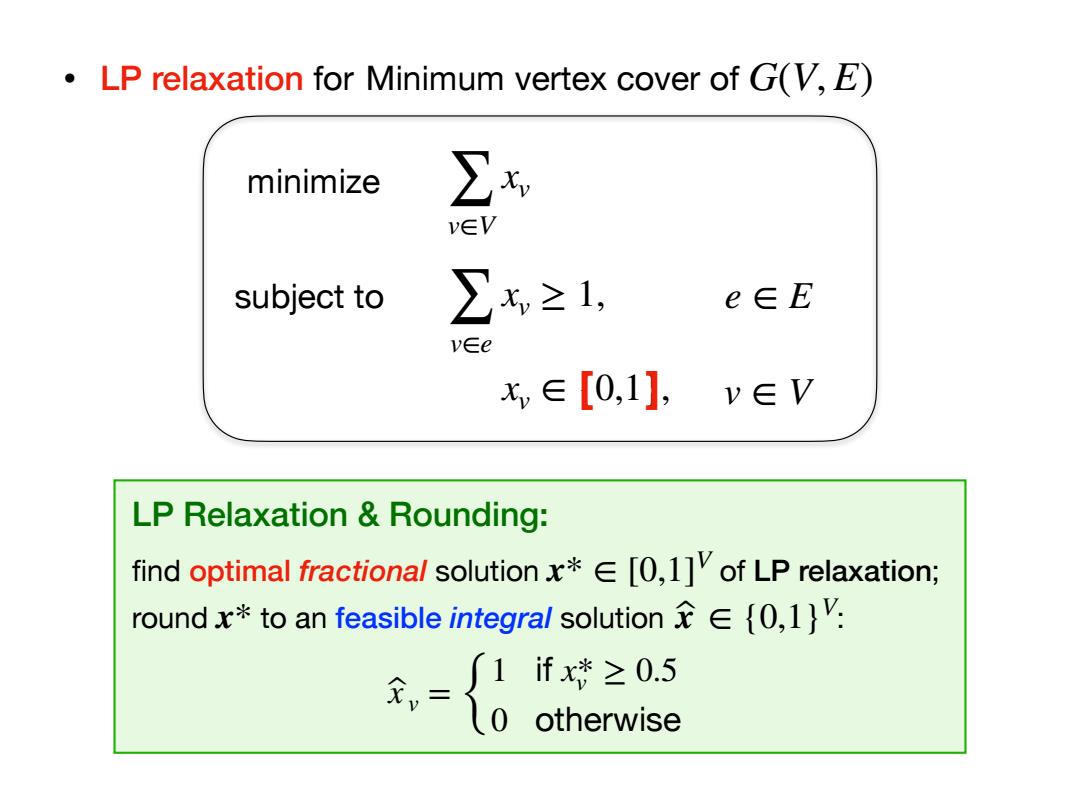
LP relaxation for Minimum vertex cover of G(V,E) minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x,∈[0,1], v∈V LP Relaxation Rounding: find optimal fractiona/solutionx*[0,1]of LP relaxation; round x*to an feasible integral solution(0,1)V: 主-{0we )otherwise
• Minimum vertex cover of G(V, E) minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V LP relaxation for [ ] LP Relaxation & Rounding: find optimal fractional solution of LP relaxation; round to an feasible integral solution : x* ∈ [0,1] V x* x ̂ ∈ {0,1}V x v ̂ = { 1 if xv * ≥ 0.5 0 otherwise
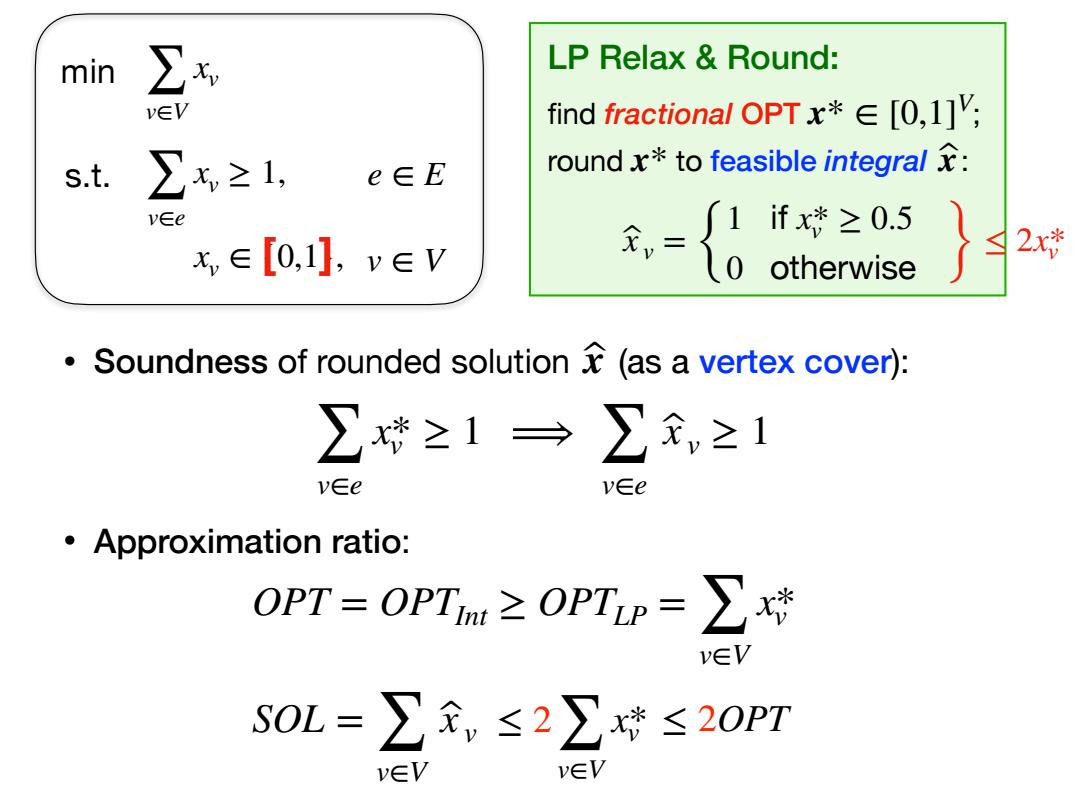
min x LP Relax Round: v∈V find fractional OPTx*E[0,1]V; s.t. ∑x≥1, e∈E round x*to feasible integral: v∈e x,∈[0,1],v∈V to cter ,={ Soundness of rounded solution (as a vertex cover): ∑特≥1→∑≥1 v∈e v∈e Approximation ratio: OPT=OPTM≥OPTP=∑x v∈V SOL=∑R,≤2∑x*≤20PT v∈V v∈V
min s.t. ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E [ ] v ∈ V LP Relax & Round: find fractional OPT ; round to feasible integral : x* ∈ [0,1] V x* x ̂ x v ̂ = { 1 if xv * ≥ 0.5 0 otherwise • Soundness of rounded solution (as a vertex cover): • Approximation ratio: x ̂ ∑ v∈e xv * ≥ 1 ⟹ ∑ v∈e x v ̂≥ 1 OPT = OPTInt ≥ OPTLP = ∑ v∈V x* v SOL = ∑ v∈V x v ̂ } ≤ 2xv * ≤ 2∑ v∈V xv * ≤ 2OPT