
10.1资产市场 资产组合 《金融经济学二 ◆ 资产组合(portfolio):对各类资产持有量组成的向量0=0.,0)7,其 中的第个元素代表第类资产持有的数量 ◆资产组合的支付 五讲》 配套课件 =x0 29 ◆资产组合的0期价值为 ∑HP,9=p9 6
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 10.1 资产市场 资产组合 ◆ 资产组合(portfolio):对各类资产持有量组成的向量θ=(θ1 , ., θJ ) T ,其 中的第j个元素代表第j类资产持有的数量 ◆ 资产组合的支付 ◆ 资产组合的0期价值为 6 1 1 1 J j j j J j S j j x x = = = xθ 1 J j j j p = = pθ

10.2完备市场和Arrow-Debreut市场 完备市场 《金融经济学二十 ◆定义10.1:我们称一个资产市场x是完备(complete)的,如果任何一个1 期的消费计划都可以通过某个资产组合来实现 ◆ 在一个完备的市场中,任给一个1期的消费计划c=(c,c,都能找到 讲》 一组组合权重0=0,O)T是下面方程组的解(其中的0是消费者持有的 资产的数量) 配套课件 5=1,2,.,S j=1 ,从经济学意义上来说,所谓完备市场,就是消费者可以通过买卖市场上 的资产,在任何两个状态之间调配资源。 ◆为什么要特别关心完备市场? 一所有的完备市场都是等价的,任意一个完备市场中得到的结论对所有完备市 场都适用。 一在完备市场中,消费者有最高的灵活度,可以实现最有效的风险的配置 一完备的市场处理起来比非完备市场容易很多一完备的市场都是一样的,但 非完备的市场各有各非完备的方式
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 10.2 完备市场和Arrow-Debreu市场 完备市场 ◆ 定义10.1:我们称一个资产市场x是完备(complete)的,如果任何一个1 期的消费计划都可以通过某个资产组合来实现 ◆ 在一个完备的市场中,任给一个1期的消费计划c=(c1 , ., cs ) T ,都能找到 一组组合权重θ=(θ1 , ., θJ ) T是下面方程组的解(其中的θj是消费者持有的 资产j的数量) ◆ 从经济学意义上来说,所谓完备市场,就是消费者可以通过买卖市场上 的资产,在任何两个状态之间调配资源。 ◆ 为什么要特别关心完备市场? – 所有的完备市场都是等价的,任意一个完备市场中得到的结论对所有完备市 场都适用。 – 在完备市场中,消费者有最高的灵活度,可以实现最有效的风险的配置 – 完备的市场处理起来比非完备市场容易很多——完备的市场都是一样的,但 非完备的市场各有各非完备的方式。 7 1 1,2, , J j s s j j c x s S = = =
10.2完备市场和Arrow-Debreut市场 完备与非完备市场示例 《金融经济学二十五讲配套课件 状态1 状态2 [] 状态1 状态2 [] B无 状态1 1 01 状态2 状态3 8
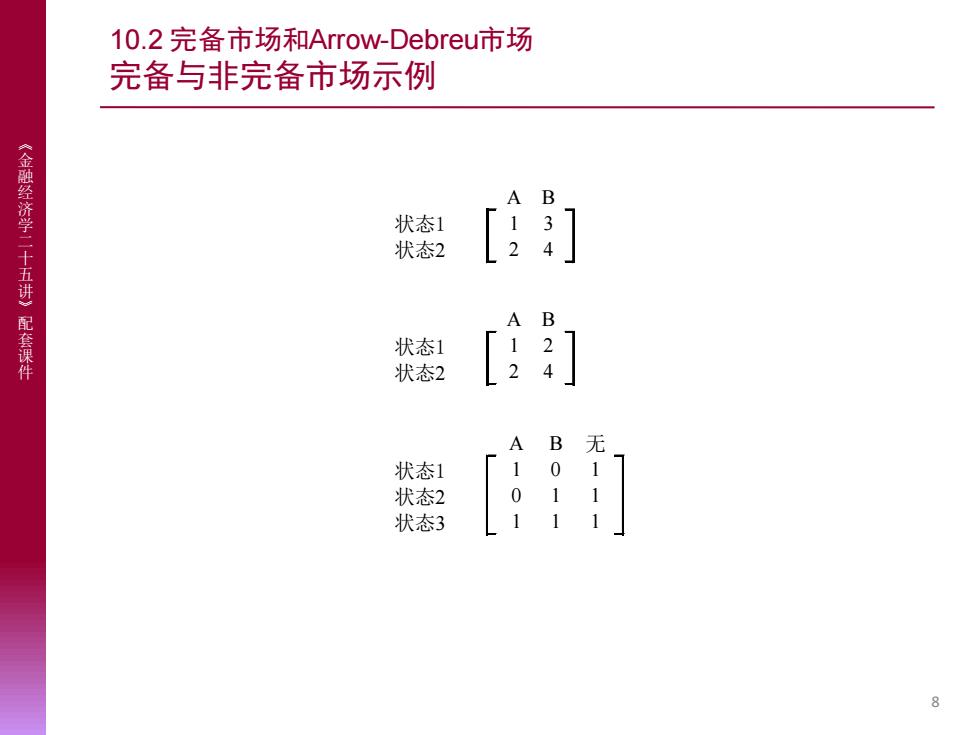
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 10.2 完备市场和Arrow-Debreu市场 完备与非完备市场示例 8 A B 状态1 1 3 状态2 2 4 A B 状态1 1 2 状态2 2 4 A B 无 状态1 1 0 1 状态2 0 1 1 状态3 1 1 1

10.2完备市场和Arrow-Debreu市场 Arrow-Debreu市场与Arrow证券 ◆Arrow-Debreu市场(Arrow-Debreu market) 《金融经济学二十五讲》 [10. 0 01. 0 I 配套课件 0 0. 1 ◆Arrowi证券(Arrow security) 0 1 1, S .: .:· 0 S
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 10.2 完备市场和Arrow-Debreu市场 Arrow-Debreu市场与Arrow证券 ◆ Arrow—Debreu市场(Arrow—Debreu market) ◆ Arrow证券(Arrow security) 9 1 0 0 0 1 0 0 0 1 I 0 1 1 0 s s S = I

10.2完备市场和Arrow-Debreut市场 Arrowi证券与资产定价 《金融经济学二 ◆ 状态价格(state price):Arow证券I,在当前(0期)的价格p,一I期某 个状态下1单位支付在0期的价格 φ≌[9. os] 五讲》 ◆资产j当前的价格(用Arrowi证券来构造资产的组合为x) 配套课件 p.w-x 所有J种资产的价格 p=0x=[px.g ]-2x.2 ◆从完备市场中S种线性无关的资产的价格反推Arow证券价格 =px- 10
《 金 融 经 济 学 二 十 五 讲 》 配 套 课 件 10.2 完备市场和Arrow-Debreu市场 Arrow证券与资产定价 ◆ 状态价格(state price):Arrow证券Is在当前(0期)的价格φs——1期某 个状态下1单位支付在0期的价格 ◆ 资产j当前的价格(用Arrow证券来构造资产j的组合为x j) ◆ 所有J种资产的价格 ◆ 从完备市场中S种线性无关的资产的价格反推Arrow证券价格 10 φ 1 S 1 S j j j s s s p x = = = φx 1 1 1 1 S S J J s s s s s s x x = = = = = p φx φx φx −1 φ = px