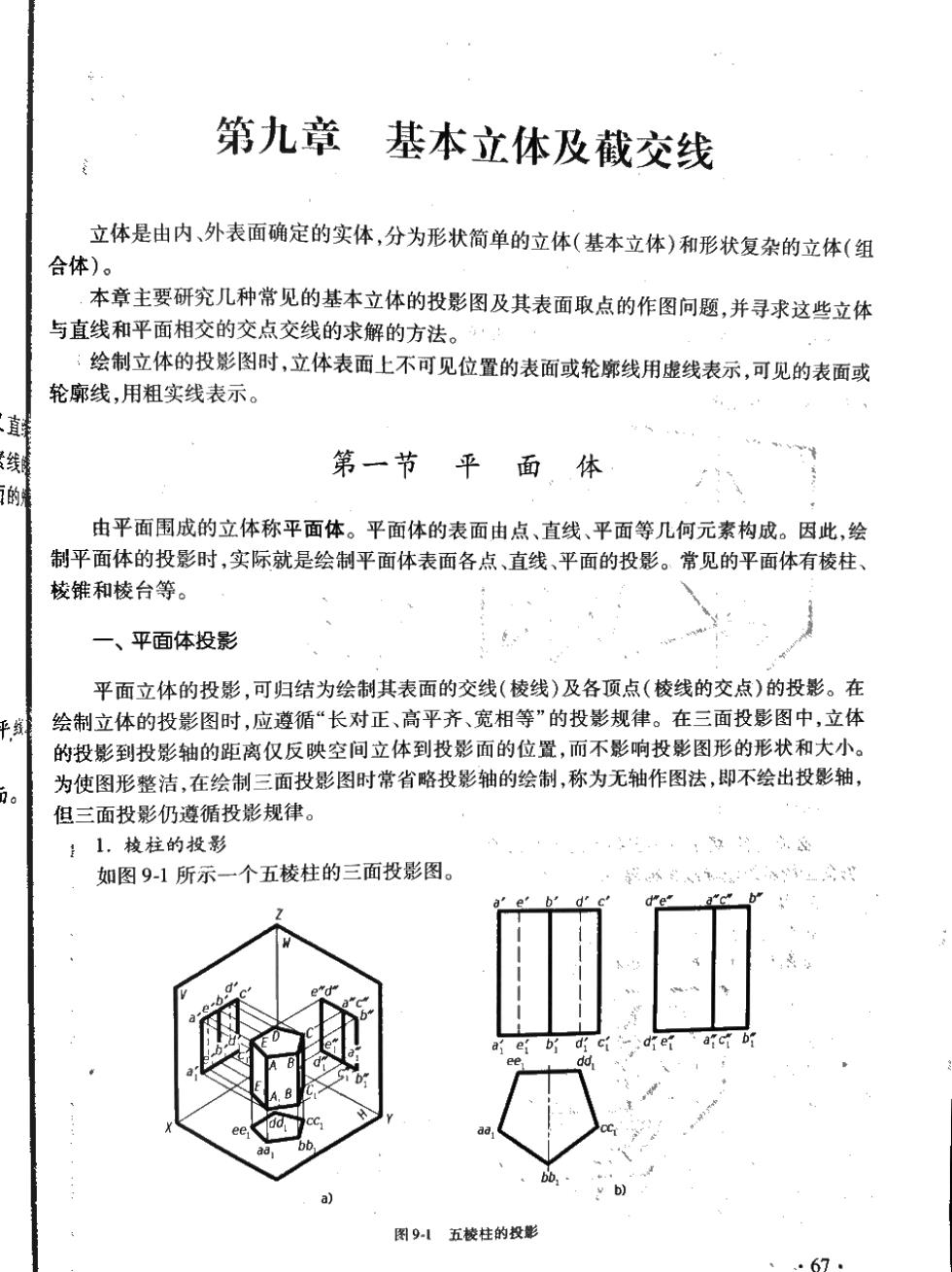
第九章 基本立体及截交线 立体是由内、外表面确定的实体,分为形状简单的立体(基本立体)和形状复杂的立体(组 合体)。 本章主要研究几种常见的基本立体的投影图及其表面取点的作图问题,并寻求这些立体 与直线和平面相交的交点交线的求解的方法。· :绘制立体的投影图时,立体表面上不可见位置的表面或轮廓线用虚线表示,可见的表面或 轮廓线,用粗实线表示。 第一节平面。体 由平面围成的立体称平面体。平面体的表面由点、直线、平面等几何元素构成。因此,绘 制平面体的投影时,实际就是绘制平面体表面各点、直线、平面的投影。常见的平面体有棱柱、 核锥和棱台等。 一、平面体投影 平面立体的投影,可归结为绘制其表面的交线(棱线)及各顶点(棱线的交点)的投影。在 绘制立体的投影图时,应遵循“长对正、高平齐、宽相等”的投影规律。在三面投影图中,立体 的投影到投影轴的距离仅反映空间立体到投影面的位置,而不影响投影图形的形状和大小。 为使图形整洁,在绘制三面投影图时常省略投影轴的绘制,称为无轴作图法,即不绘出投影轴, 但三面投影仍遵循投影规律。 :1.梭柱的投影 如图91所示一个五棱柱的三面投影图。 图91五棱柱的投影 .67
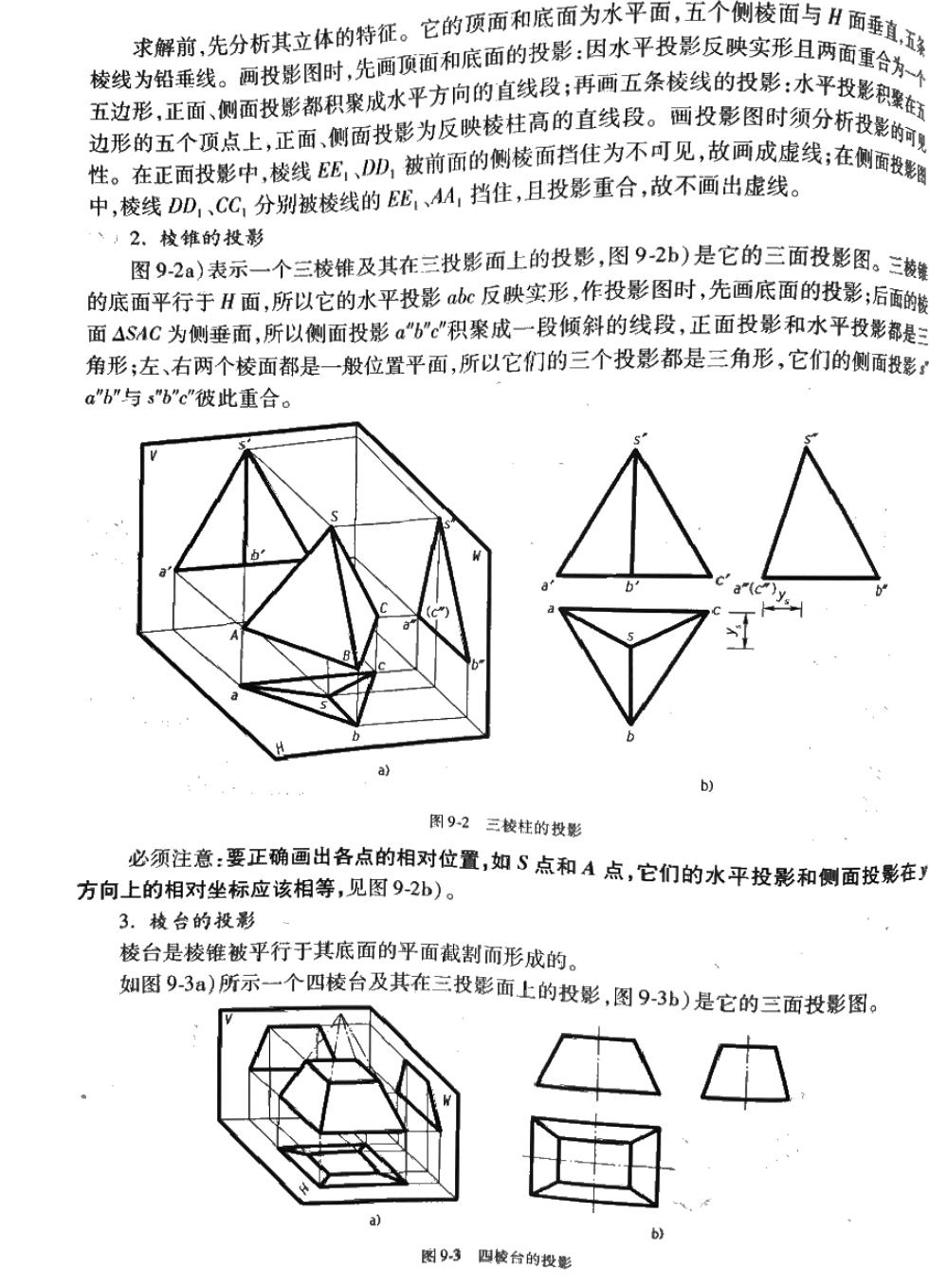
、求解前,先分析其立体的特征。它的顶面和底面为水平面,五个侧棱面与H面垂直 装线务餐案设生分投影闲时先周顶面和底面的投影:团水平投影反晚实形日两看美重合养 院资花载闲需投影布只聚成水平方向的直线段:有新五条技线的投影水平技彩感女 边形的五个顶点上。正面、侧面投影为反映校柱高的直线段。面投影因时颈分析授影 性。在正而投影中,楼线出,、DM,被前面的侧棱面挡住为不可见,故面成虚线:在侧面数 中,棱线DD,、CC,分别被棱线的EE,AM,挡住,且投影重合,故不画出虚线。 ,2.校锥的投影 图9.2a)表示一个三棱排及其在三投影面上的投影,图9:2b)是它的三面投影图。三黄 的底面平行于H面,所以它的水平投影反映实形,作投影图时,先画底面的投影;后 面4S4C为侧垂面,所以侧面投影c积聚成一段倾斜的线段,正面投影和水平投影都是: 角形;左、右两个棱面都是一般位置平面,所以它们的三个投影都是三角形,它们的侧面投影: a"6”与s"bc"彼此重合。 图92三校柱的投影 必须注意:要正确画出各点的相对位置,如S点和A点,它们的水平投影和侧面投影在) 方向上的相对坐标应该相等,见图92b)。 3.棱台的投影 棱台是棱锥被平行于其底面的平面裁割而形成的。 如图93a)所示一个四棱台及其在三投影面上的投影,图9-3b)是它的三面投影图。 图93四棱台的投影
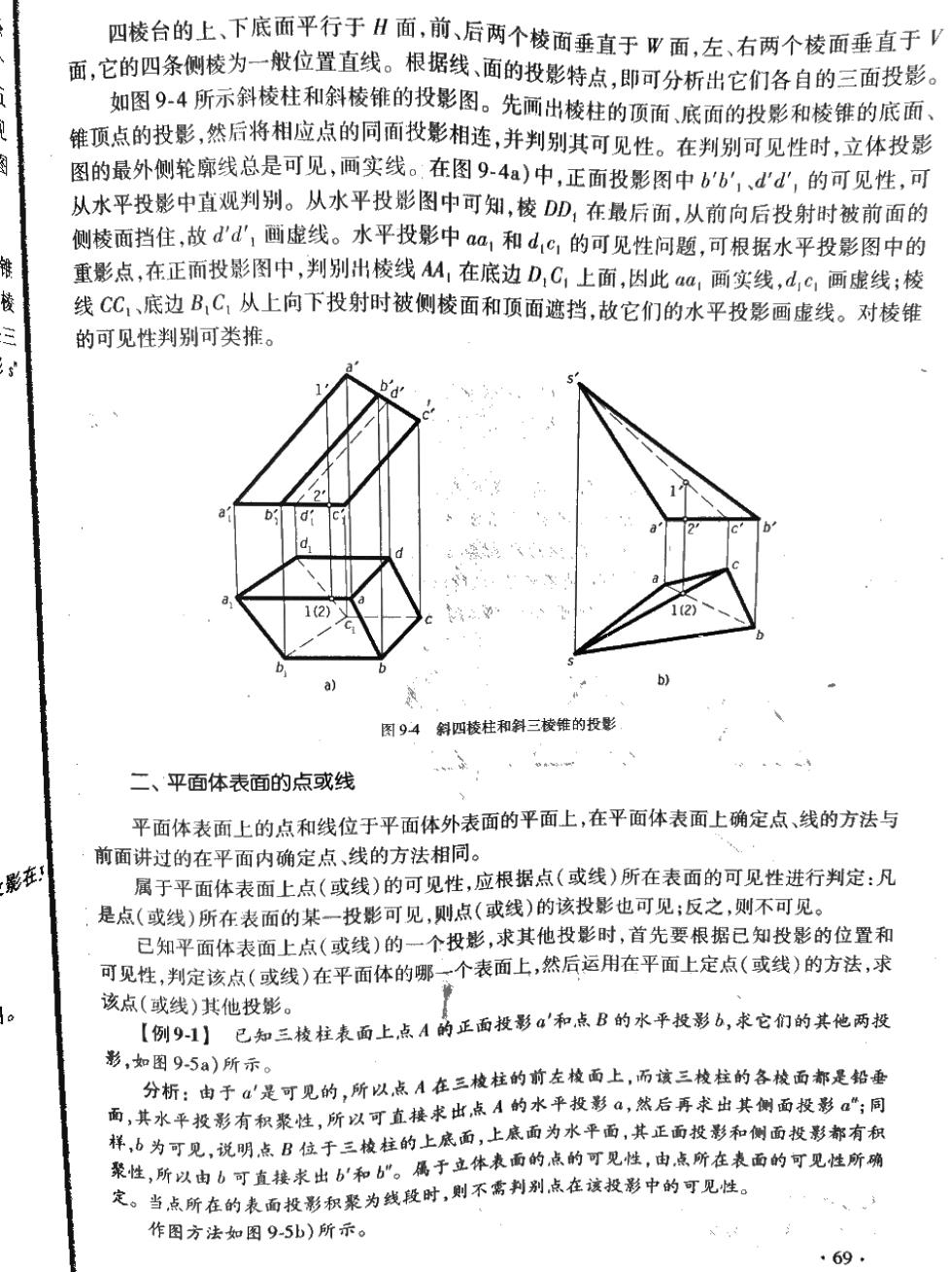
四棱台的上、下底面平行于H面,前、后两个棱面垂直于?面,左、右两个棱面垂直于V 面,它的四条侧棱为一般位置直线。根据线,面的投影特点,即可分析出它们各自的三面投影。 ”如图9-4所示斜棱柱和斜棱锥的投影图。先雨出棱柱的顶而底而的投影和棱锥的底面 锥顶点的投影,然后将相应点的同面投影相连,并判别其可见性。在判别可见性时,立体投影 图的最外侧轮廓线总是可见,画实线。在图94a)中,正面投影图中b6,d心d,的可见性,可 从水平投影中直观判别。从水平投影图中可知,棱DD,在最后面,从前向后投射时被前面的 侧棱面挡住,故d'd画虚线。水平投影中aa,和d,c,的可见性问题,可根据水平投影图中的 重影点,在正面投影图中,判别出棱线M,在底边D,C,上面,因此,商实线,dG,画虚线;棱 线CC,、底边B,C,从上向下投射时被侧棱面和顶面遮挡,故它们的水平投影画虚线。对棱锥 的可见性判别可类推。 图94斜四棱柱和斜三棱锥的投影 二、平面体表面的点或线 平面体表面上的点和线位于平面体外表面的平面上,在平面体表面上确定点、线的方法与 前面讲过的在平面内确定点、线的方法相同。 影在 属于平面体表面上点(或线)的可见性,应根据点(或线)所在表面的可见性进行判定:凡 是点(或线)所在表面的某一投影可见,则点(或线)的该投影也可见;反之,则不可见。 已知平面体表面上点(或线)的一个投影,求其他投影时,首先要根据己知投影的位置和 可见性,判定该点(或线)在平面体的哪个表面上,然后运用在平面上定点(或线)的方法,求 该点(或线)其他投影。 【例91】已知三被柱表面上点A的正面授影a和点B的水平投影6,求它们的其他两投 形,如图95a)所示。 分析:由子'是可见的,所以,点A在三校柱的前左枚面上,而该三棱柱的各被西都是铅垂 面,其水平投形有积聚性,所以可直排求出减A的水平投影,然后再求出其侧西授形a同 样,6为可见,说明点B位于三检柱的上底面,上底面为水平面,其正面投影和侧面授影都有积 聚性,所以由6可直接求出6和6。属于立体表面的点的可见性,由成所在表面的可见性所动 定。当,点所在的表面投形积聚为线设时,则不需判别点在演投影中的可见性。 作图方法如图95b)所示。 69

图95棱柱表面上的点 【例92】已知三棱维表面上的点K和线段MN的正面投影k和m'n',如图96a)所示 求作它们的其他两投影。 分析:从图中可以看出,k是可见的,所以点K在三棱雏表面SBC上,过点K在SBC上 作一条辅助线,例如SD,求出SD的各投影,点K的各投影即在线段SD的同面投影上。 作图:过k'作'd”,求出sd和"”,然后在sd和s"”上分别作出k和k"[图9-6b)]。由于 点及所在表面SBC的侧面投影sbc”是不可见的,所以"也是不可见的。 同样,包含直线MN作辅助线,即可求出MN的其他各投影。具体作图见图9-6b) 图96棱锥表面上的点和线 三、平面体的截交线 在求解丁程上某些空间儿何问题时,常常会碰到平面与立休相交的同题。当平面体被子 面载切生款交线,加图97所示,被切立体的平面P称为酸平面交能平面P与平面之体名 表面的交线称为我交线:数文线是由那些概在裁平面上又在立体发面的点集合领断文 文线实际上是求货子面和立体表面的共有点的问蓝。极交线所价成的的能斧为版面斯 截交线是一个封团的平面多边形。求截交线,实际就是求出各棱面与截平面的交线:成者求音 棱线与截平面的交点,并依次连接同一棱面上的两交点,然后按其可加与不可见用粗实线或嘘。 线依次相连得到截交线。 ,70

平面与平面立体相交,其截交线形状是由直线段组成的多边形。多边形的预点为平面立 体上有关棱线(包括底面边线)与截平面的交点。其具体求法分为以下两种情况: 1.特殊位置平面与平面立体相交N 由于特殊位置平面的某些投影有积聚性,所以平面立体的棱线与其交点的投影,可直接利 用积聚性求出。 2.一般位置平面与平面立体相交 一般位置平面的各投影都没有积聚性,求平面立体上棱线与其交点,用一般位置直线与一 般位置平面相交的方法求解,即用包含棱线作辅助平面的方法求出。 本节主要介绍第一种情况的作图。 【例93】如图97所示,求正垂面P与三棱维的栽交线。 分析:截平面P与三棱维的三条校线SA、SB、SC相交,可采用求棱线与截平面交点的方 法,分别求出三条棱线与裁平面的交点I、Ⅱ、Ⅲ,连接起来即为截交线。 作图:裁平面是正垂面,它的正面投影有积聚性,而交点是戴平面与棱线的公有点,所以从 正面投影可以直接得出三条棱线与截平面交点的正面投影1'、2'3'。由1'、2'、3可以求出交 点的其他投影123和1”2”3”。依次连接各点的同名投影,即得出藏交线的各授影。具体 作图见图97(此处未画出侧面投影)。 图97三棱维的截交 判定可见性:因为截交线所在的三个被面的水平投影是可见的,所以藏交线的水平授影也 是可见的;而被面SMC和SBC的侧面投影是不可见的,所以藏交线13"和2了"也是不可见的。 【例94)】如困98a)所示,求四棱柱被裁切后的三面投影围及我面的实形。 分析:戴平西P与四校柱的4个枚面发上底面相交,所以藏交线是一个凸五边形。它的五个顶 点分别是栽平面与四被柱三条校线及上底面的两条边线的交.点。由于平面P为正垂面,所以栽交 线的正面投影重合于P,。四校柱的各棱面为铅垂面,它们与平面P文线的水平投影和各棱西的水 平授影重合。藏平面与被柱上底面的交线为正垂线,其正面投影积聚为一点,水平投影反映实长。 根据对正面授影和水平投影的分析,可知交线的侧西投影是比实形缩小的五边形。 作图[图9.8b)]: ((1)作出四校柱未栽切时的侧面投影。 (2)从正面投影可以直接得到P平面与3条棱线交点的投影b,,从而求出其侧面投 形。b、C。 ·71