电子科技大学：《高等电磁场理论》课程教学资源（课件讲稿）第一章 基本电磁理论

第一章」 基本电做理论 名等电喊场理论 2、对偶原理 源：电荷p、电流了 磁荷p"、磁流了m 产生场：E、H、D、Be Em、Hm、Dm、Bm vxm=j+ D aDm Ot Ot 方程：下 aB at V×Em=-j- @Bm Ot 7.Be=0 V.Bm=pm V.D-p 7.Dm=0 对偶关系：J Hm-Em

第一章 基本电磁理论 高等电磁场理论 产生场： m m m m E H D B e e e e 、 、 、 E H D B 、 、 、 m m m m m m m m 0 D H t B E J t B D       =       = − −      =     = e e e e e e 0 D H J t B E t B D       = +       = −      =     = 方程： 2、对偶原理 对偶关系： 电荷  、电流 J 磁荷 、磁流 m J m 源：  e E e H e D e J B  m H m −E m B m −D m J m     

第一章 基本电做理论 高等电赋场理论 3、广义的麦克斯韦方程组 V×H=j+ ∂D 8t aB 时域 V×E=-jm- H=H+Hm Ot V·B=pm =Ee+m 其中： V.D-P B=B e+Bm V×H=J+joD D=D+Dm 频域 V×E=-Jm-joB V.B=p" V.D=p

第一章 基本电磁理论 高等电磁场理论 m m D H J t B E J t B D        = +        = − −     =     = e m e m e m e m H H H E E E B B B D D D  = +   = +   = +   = + 其中： 3、 广义的麦克斯韦方程组 时域 m m H J j D E J j B B D       = +     = − −     =     = 频域

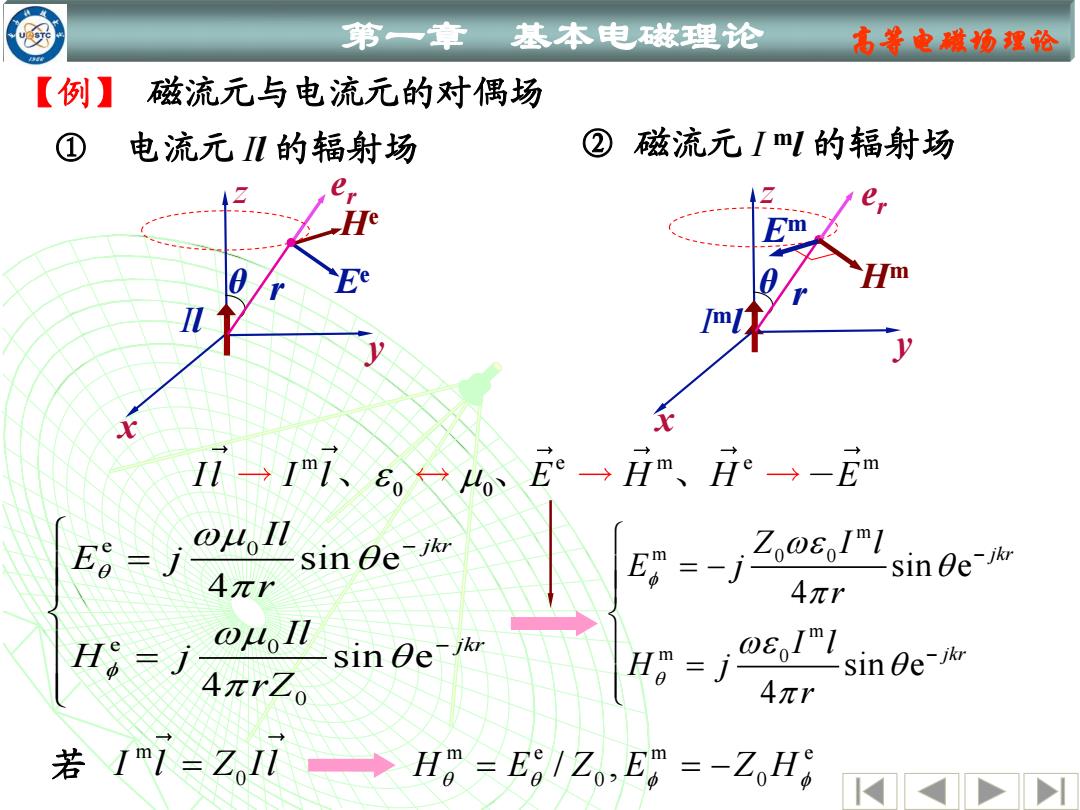
第一章」 基本电磁理论 名等电喊场理论 【例】 磁流元与电流元的对偶场 ① 电流元I几的辐射场 ② 磁流元ImL的辐射场 1i-17、6,4E→im、H→-E E8=j ol 4元r sin e-ikr sin e-ikr 4πr o41I1 H8=j4πrZ。 sin e-ikr 8I H。=j sin de-jkr 4πr 若Im1=ZIl ◆H=E61Zo,E=-ZH8

第一章 基本电磁理论 高等电磁场理论 e 0 e 0 0 sin e 4 sin e 4 jkr jkr Il E j r Il H j rZ           − −  =     =  ① 电流元 Il 的辐射场 ② 磁流元 I ml 的辐射场 m m 0 0 m m 0 sin e 4 sin e 4 jkr jkr Z I l E j r I l H j r           − −  = −     =  m e m e m Il I l E H H E 、   、 、 e z r x y θ r Il Ee He z I ml x y r θ er Hm Em 若 m 0 I l Z Il = m e m e 0 0 H E Z E Z H / ,     = = − 【例】 磁流元与电流元的对偶场

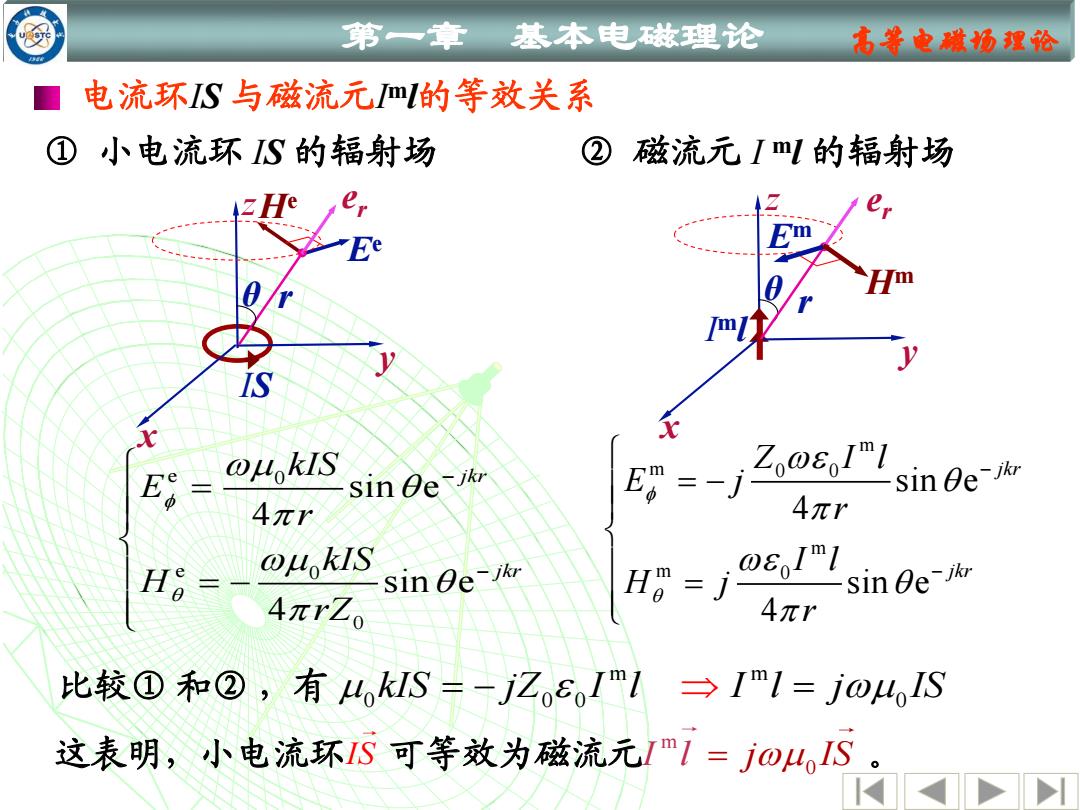
第一章 基本电磁理论 高等电赋场理论 电流环IS与磁流元m的等效关系 ①小电流环S的辐射场 ② 磁流元ImL的辐射场 m IS e oukIS sin Oejkr sin e- 4πr 4πr H8= oukIS sin Oe-ik 6,I" 4πrZ Ho=j sin e-skr 4元r 比较①和②，有4IS=-jZosoI"1→Im1=j04IS 这表明，小电流环IS可等效为磁流元m1=j04IS

第一章 基本电磁理论 高等电磁场理论 电流环IS 与磁流元I ml的等效关系 ② 磁流元 I ml 的辐射场 m m 0 0 m m 0 sin e 4 sin e 4 jkr jkr Z I l E j r I l H j r           − −  = −     =  z I ml x y r θ er Hm Em ① 小电流环 IS 的辐射场 e 0 e 0 0 sin e 4 sin e 4 jkr jkr kIS E r kIS H rZ           − −  =     = −  IS x y z θ r er Ee He 比较① 和② ，有 m m 0 0 0 0    kIS jZ I l I l j IS = −  = 这表明，小电流环IS 可等效为磁流元 0 。 m I l = j I  S

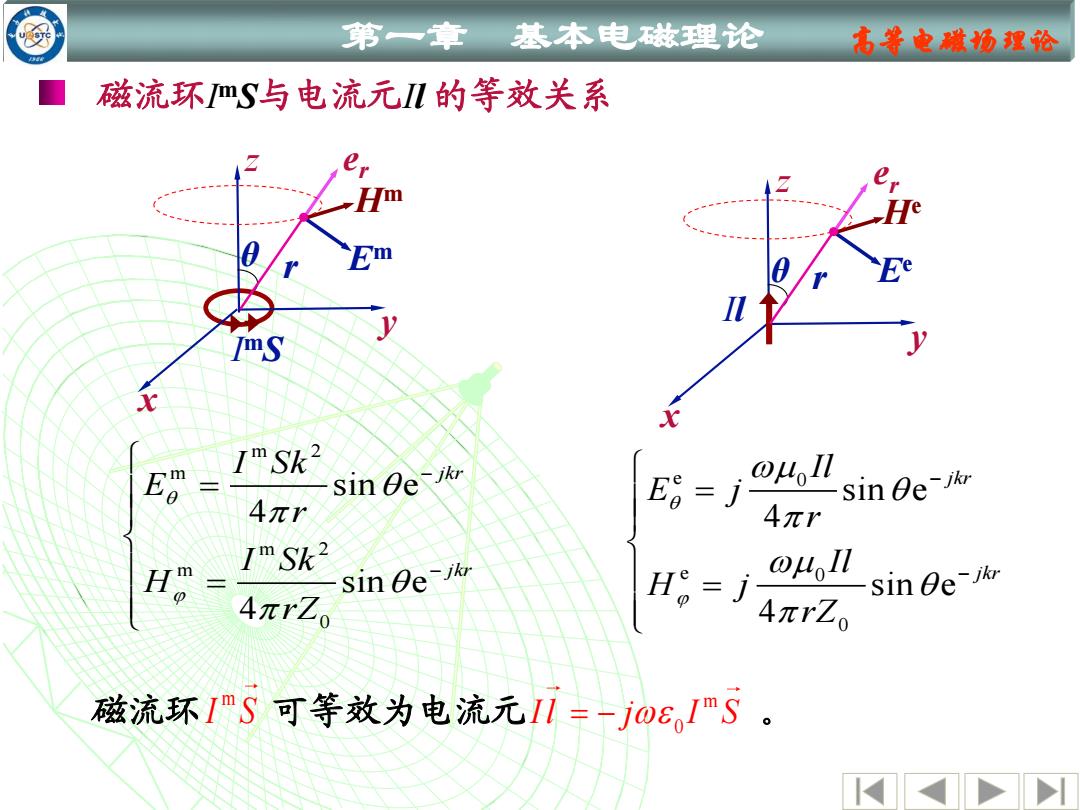
第一章 基本电做理论 高等电赋场理论 磁流环mS与电流元I几的等效关系 Hm ImSk2 sin Oe -jkr 4πr @u,Lsin0e☆ 4πr ImSk2 sin e-ikr uon 4πrZ0 H=j sin ge-ikr 元rZ。 磁流环ImS可等效为电流元Il=-j06ImS

第一章 基本电磁理论 高等电磁场理论 m 0 I l j I S = −  m 磁流环 I S 可等效为电流元 。 磁流环I mS与电流元Il 的等效关系 e 0 e 0 0 sin e 4 sin e 4 jkr jkr Il E j r Il H j rZ           − −  =     =  m 2 m m 2 m 0 sin e 4 sin e 4 jkr jkr I Sk E r I Sk H rZ       − −  =     =   I mS x y z r θ er Hm Em e z r x y θ r Il Ee He