
例椭圆规的曲柄OC可绕定轴O转动,其端点C与 规尺AB的中点以铰链相连接,而规尺A,B两端分别 在相互垂直的滑槽中运动。 已知:OC=AC=BC=l,MC=a,p=t 求:1.M点 的运动方程; B 2.轨迹; 3.速度; 4.加速度
例 椭圆规的曲柄OC 可绕定轴O 转动,其端点C 与 规尺AB 的中点以铰链相连接,而规尺A,B 两端分别 在相互垂直的滑槽中运动。 已知:OC = AC = BC = l,MC = a, =t 求:1.M 点 的运动方程; 2. 轨迹; 3. 速度; 4. 加速度

解:点Mc,y)作曲线运动,取坐标系xoy 运动方程 x=(OC+CM)cos=(1+a)cosot y=AM sin =(1-a)sin ot 消去t,得轨迹 x2
解:点M(x,y)作曲线运动,取坐标系xoy 运动方程 x = (OC +CM) cos = (l + a) cost y = AM sin = (l − a)sin t 消去t, 得轨迹 1 ( ( ) 2 2 2 2 = − + + l a y l a x )
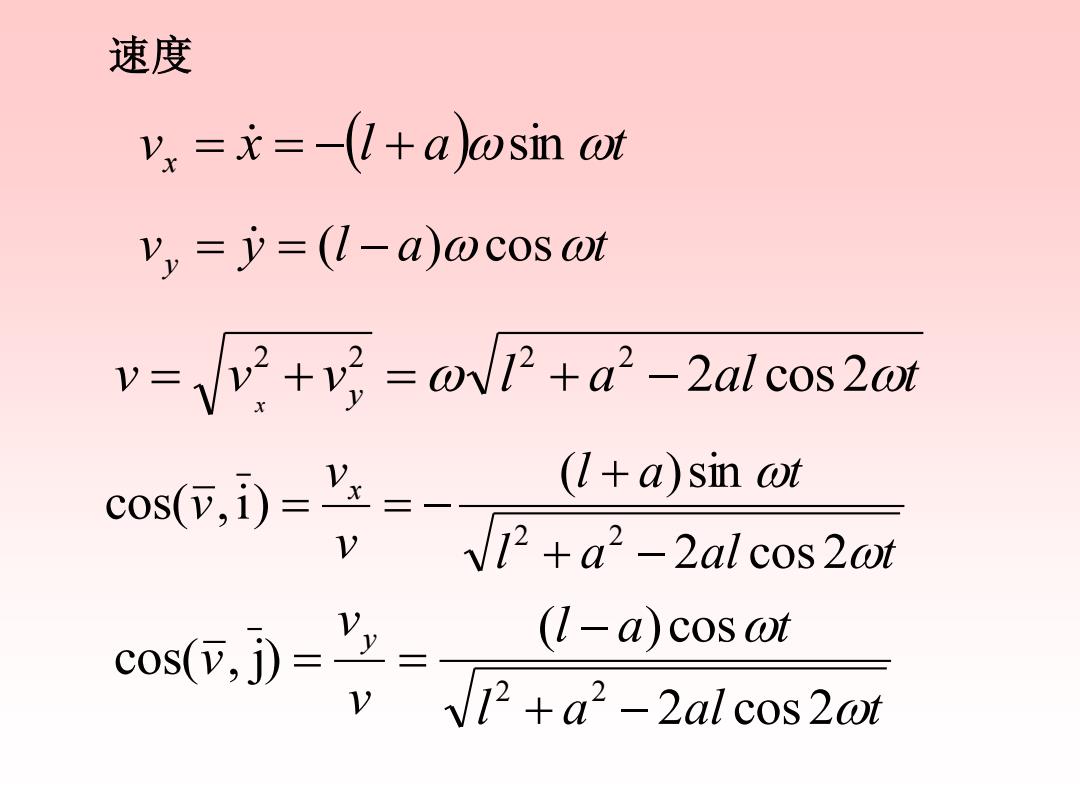
速度 vs ==-(l+a)osin at vy=y=(l-a)ocosot v=v+v;=@vP+a"-2alcos2@r cos(,i)=业= (1+a)sin at 12+a2 -2al cos 2wt co.) (1-a)cosat 12+a2-2al cos2@t
速度 v x (l a) t x = = − + sin v y l a t y = = ( − ) cos l a al t l a t v v v x 2 cos 2 ( )sin cos( ,i) 2 2 + − + = = − l a al t l a t v v v y 2 cos 2 ( ) cos cos( , j) 2 2 + − − = = v v v l a al t y x 2 cos 2 2 2 2 2 = + = + −