
Remove nonreasonable nash equilibrium 0 Subgame perfect Nash equilibrium is a refinement of Nash equilibrium It can rule out nonreasonable Nash equilibria or non-creditable threats We first need to define subgame 22
Remove nonreasonable Nash equilibrium ◼ Subgame perfect Nash equilibrium is a refinement of Nash equilibrium ◼ It can rule out nonreasonable Nash equilibria or non-creditable threats ◼ We first need to define subgame 22
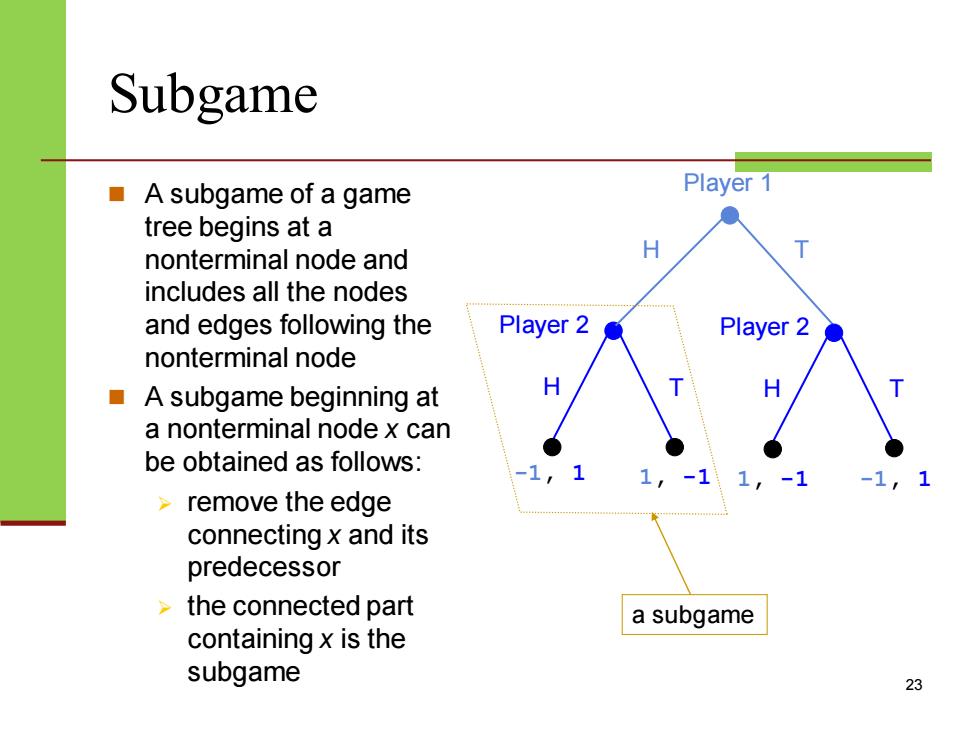
Subgame ■A subgame of a game Player 1 tree begins at a nonterminal node and H includes all the nodes and edges following the Player 2 Player 2 nonterminal node A subgame beginning at a nonterminal node x can be obtained as follows: remove the edge connecting x and its predecessor the connected part a subgame containing x is the subgame 23
Subgame ◼ A subgame of a game tree begins at a nonterminal node and includes all the nodes and edges following the nonterminal node ◼ A subgame beginning at a nonterminal node x can be obtained as follows: ➢ remove the edge connecting x and its predecessor ➢ the connected part containing x is the subgame 23 -1, 1 Player 1 Player 2 H T 1, -1 H T Player 2 H T 1, -1 -1, 1 a subgame
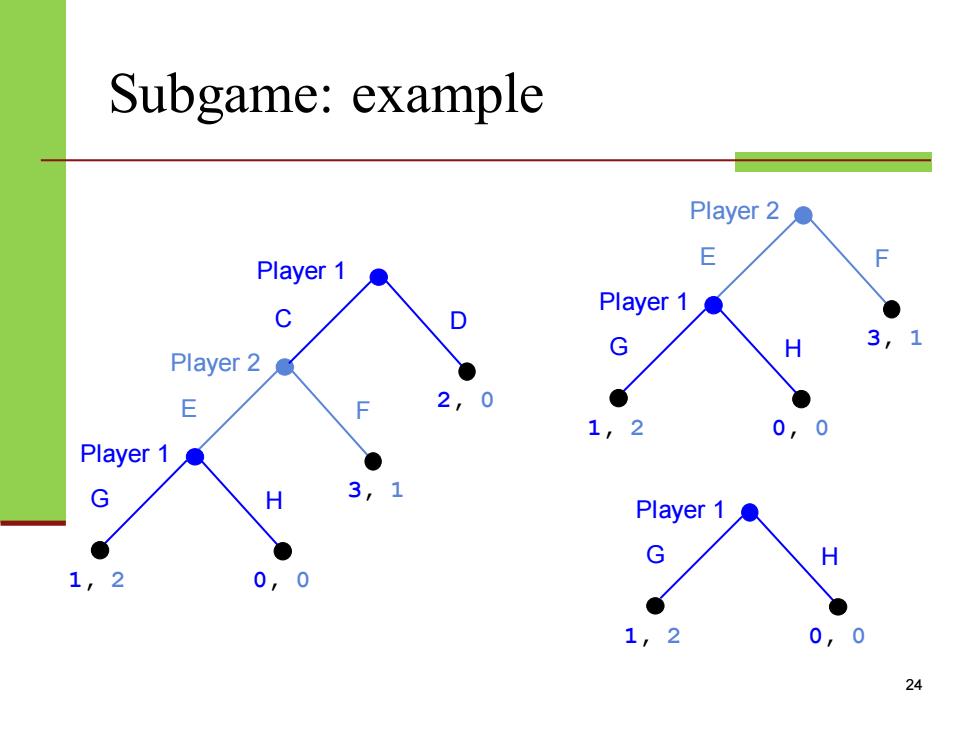
Subgame:example Player 2 Player 1 E C Player 1 Player 2 E 0 0 Player 1 H Player 0 0, 0 24
Subgame: example 24 Player 2 E F Player 1 G H 3, 1 1, 2 0, 0 Player 1 C D 2, 0 Player 2 E F Player 1 G H 3, 1 1, 2 0, 0 Player 1 G H 1, 2 0, 0

Subgame-perfect Nash equilibrium A Nash equilibrium of a dynamic game is subgame-perfect if the strategies of the Nash equilibrium constitute a Nash equilibrium in every subgame of the game. Subgame-perfect Nash equilibrium is a Nash equilibrium. 25
Subgame-perfect Nash equilibrium ◼ A Nash equilibrium of a dynamic game is subgame-perfect if the strategies of the Nash equilibrium constitute a Nash equilibrium in every subgame of the game. ◼ Subgame-perfect Nash equilibrium is a Nash equilibrium. 25
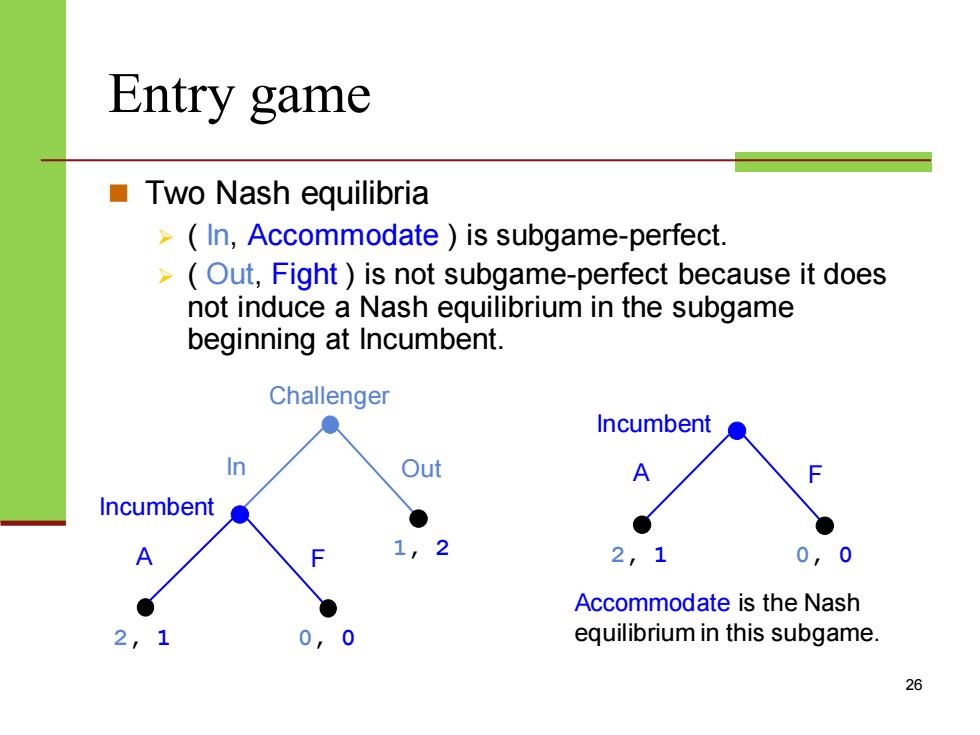
Entry game ■Two Nash equilibria In,Accommodate is subgame-perfect. -Out,Fight is not subgame-perfect because it does not induce a Nash equilibrium in the subgame beginning at Incumbent. Challenger Incumbent n Out Incumbent 1,2 2, 0,0 Accommodate is the Nash 2 01 0 equilibrium in this subgame. 26
Entry game ◼ Two Nash equilibria ➢ ( In, Accommodate ) is subgame-perfect. ➢ ( Out, Fight ) is not subgame-perfect because it does not induce a Nash equilibrium in the subgame beginning at Incumbent. 26 Challenger In Out Incumbent A F 1, 2 2, 1 0, 0 Incumbent A F 2, 1 0, 0 Accommodate is the Nash equilibrium in this subgame