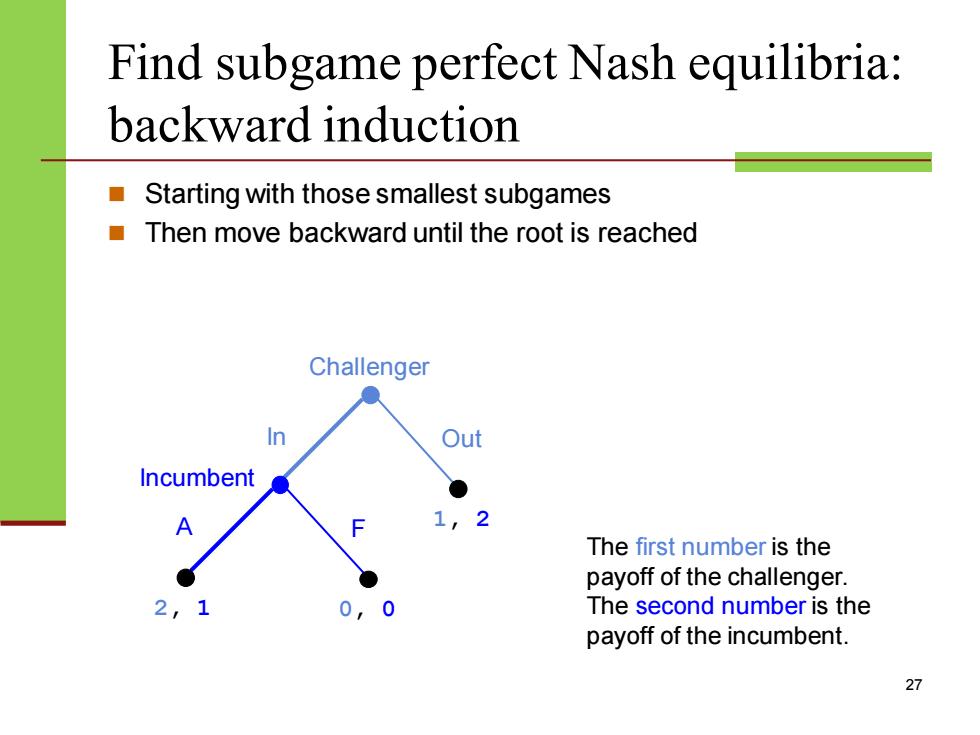
Find subgame perfect Nash equilibria: backward induction Starting with those smallest subgames Then move backward until the root is reached Challenger In Out Incumbent F 11 2 The first number is the payoff of the challenger. 01 The second number is the payoff of the incumbent. 27
Find subgame perfect Nash equilibria: backward induction ◼ Starting with those smallest subgames ◼ Then move backward until the root is reached 27 Challenger In Out Incumbent A F 1, 2 2, 1 0, 0 The first number is the payoff of the challenger. The second number is the payoff of the incumbent
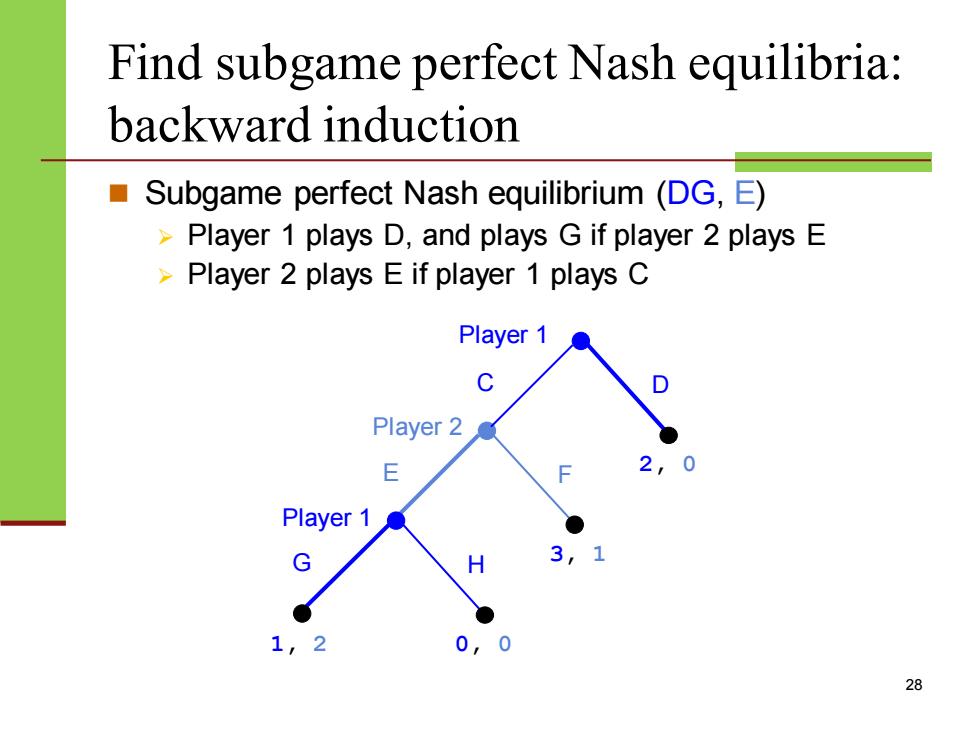
Find subgame perfect Nash equilibria: backward induction ■} Subgame perfect Nash equilibrium (DG,E) -Player 1 plays D,and plays G if player 2 plays E -Player 2 plays E if player 1 plays C Player 1 C Player 2 E Player 1 3 0 28
Find subgame perfect Nash equilibria: backward induction ◼ Subgame perfect Nash equilibrium (DG, E) ➢ Player 1 plays D, and plays G if player 2 plays E ➢ Player 2 plays E if player 1 plays C 28 Player 2 E F Player 1 G H 3, 1 1, 2 0, 0 Player 1 C D 2, 0

Existence of subgame-perfect Nash equilibrium Every finite dynamic game of complete and perfect information has a subgame-perfect Nash equilibrium that can be found by backward induction. 汤
Existence of subgame-perfect Nash equilibrium ◼ Every finite dynamic game of complete and perfect information has a subgame-perfect Nash equilibrium that can be found by backward induction. 29

Sequential bargaining (2.1.D of Gibbons) Player 1 and 2 are bargaining over one dollar.The timing is as follows: At the beginning of the first period,player 1 proposes to take a share s,of the dollar,leaving 1-s,to player 2. Player 2 either accepts the offer or rejects the offer(in which case play continues to the second period) At the beginning of the second period,player 2 proposes that player 1 take a share s2 of the dollar,leaving 1-s2 to player 2. Player 1 either accepts the offer or rejects the offer(in which case play continues to the third period) At the beginning of third period,player 1 receives a share s of the dollar,leaving 1-s for player 2,where 0<s <1. The players are impatient.They discount the payoff by a fact, where0<δ<1 30
Sequential bargaining (2.1.D of Gibbons) ◼ Player 1 and 2 are bargaining over one dollar. The timing is as follows: ◼ At the beginning of the first period, player 1 proposes to take a share s1 of the dollar, leaving 1-s1 to player 2. ◼ Player 2 either accepts the offer or rejects the offer (in which case play continues to the second period) ◼ At the beginning of the second period, player 2 proposes that player 1 take a share s2 of the dollar, leaving 1-s2 to player 2. ◼ Player 1 either accepts the offer or rejects the offer (in which case play continues to the third period) ◼ At the beginning of third period, player 1 receives a share s of the dollar, leaving 1-s for player 2, where 0<s <1. ◼ The players are impatient. They discount the payoff by a fact , where 0< <1 30

Sequential bargaining (2.1.D of Gibbons) Player 1 propose an offer(s1,1-s1) Period 1 Player 2 accept ●s1,1-s1 reject Player 2 propose an offer (s2 1-s2) Period 2 Player 1 ●52,1-s2 accept reject Period 3 ,1-s 31
Sequential bargaining (2.1.D of Gibbons) 31 Player 2 accept reject propose an offer ( s2 , 1-s2 ) Period 1 Player 1 accept propose an offer ( s1 , 1-s1 ) s1 , 1-s1 Player 1 s2 , 1-s2 s , 1-s Period 2 Period 3 reject Player 2