
Sequential-move matching pennies Player 1's strategies Head >Tail Player 2's strategies -H if player 1 plays H,H if player 1 plays T >H if player 1 plays H,T if player 1 plays T T if player 1 plays H,H if player 1 plays T T if player 1 plays H,T if player 1 plays T Player 2's strategies are denoted by HH,HT,TH and TT,respectively.(n x m) >
Sequential-move matching pennies ◼ Player 1’s strategies ➢ Head ➢ Tail ◼ Player 2’s strategies ➢ H if player 1 plays H, H if player 1 plays T ➢ H if player 1 plays H, T if player 1 plays T ➢ T if player 1 plays H, H if player 1 plays T ➢ T if player 1 plays H, T if player 1 plays T Player 2’s strategies are denoted by HH, HT, TH and TT, respectively.(n x m) 17
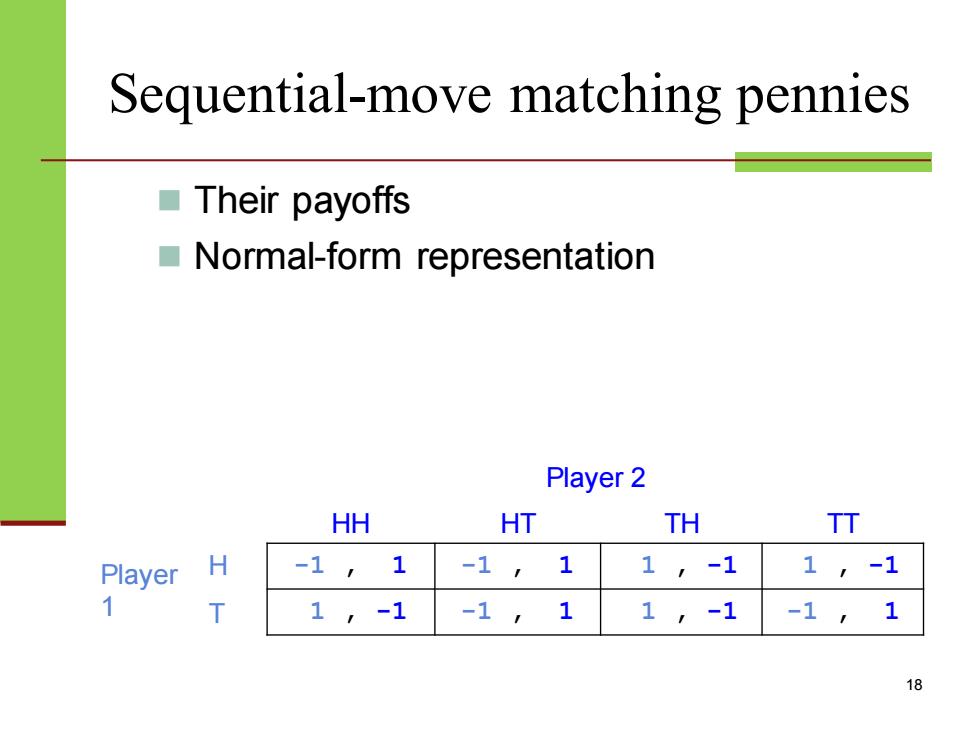
Sequential-move matching pennies Their payoffs Normal-form representation Player 2 HH HT TH TT Player H -1 ,1 -1, 1 ,-1 1 1,-1 T 1,-1 -1, 1 1,-1 -1 18
Sequential-move matching pennies Player 2 HH HT TH TT Player 1 H -1 , 1 -1 , 1 1 , -1 1 , -1 T 1 , -1 -1 , 1 1 , -1 -1 , 1 18 ◼ Their payoffs ◼ Normal-form representation

Nash equilibrium The set of Nash equilibria in a dynamic game of complete information is the set of Nash equilibria of its normal-form. 19
Nash equilibrium ◼ The set of Nash equilibria in a dynamic game of complete information is the set of Nash equilibria of its normal-form. 19

Nash equilibrium in a dynamic game We can also use normal-form to represent a dynamic game The set of Nash equilibria in a dynamic game of complete information is the set of Nash equilibria of its normal-form How to find the Nash equilibria in a dynamic game of complete information Construct the normal-form of the dynamic game of complete information >Find the Nash equilibria in the normal-form 20
Nash equilibrium in a dynamic game ◼ We can also use normal-form to represent a dynamic game ◼ The set of Nash equilibria in a dynamic game of complete information is the set of Nash equilibria of its normal-form ◼ How to find the Nash equilibria in a dynamic game of complete information ➢ Construct the normal-form of the dynamic game of complete information ➢ Find the Nash equilibria in the normal-form 20

Nash equilibria in entry game ■Two Nash equilibria In,Accommodate >Out,Fight Does the second Nash equilibrium make sense? Non-creditable threats Limitation to the normal form representation Incumbent Accommodate Fight In 2,1 0, 0 Challenger Out 1, 2 1,2 21
Nash equilibria in entry game Incumbent Accommodate Fight Challenger In 2 , 1 0 , 0 Out 1 , 2 1 , 2 21 ◼ Two Nash equilibria ➢ ( In, Accommodate ) ➢ ( Out, Fight ) ◼ Does the second Nash equilibrium make sense? ◼ Non-creditable threats ◼ Limitation to the normal form representation