
db 2g(l+r) dt' y2+21+r列8=0 比较上两式得到: 2g(1+r) 2(l+r) 由: 2g(l+r) 可得r与1的关系式: 6π2r2+4π212+8π21r-g1-9r=0 返回
+ q r g l r 2 2 ( ) + + =0 2 (l +r ) 2 dq dt 2 2 = r g l r 2 2 ( ) + 2 + 2(l +r ) ω = r g l r 2 2 ( ) + 2 + 2(l +r ) r 2 6π + gl =0 2 l 2 4π 2 l r 2 + 8π gr 可得 r 与 l 的关系式: = ω 由: T 2π =1 + q 2 =0 2 dq dt 2 ω 比较上两式得到: 返回
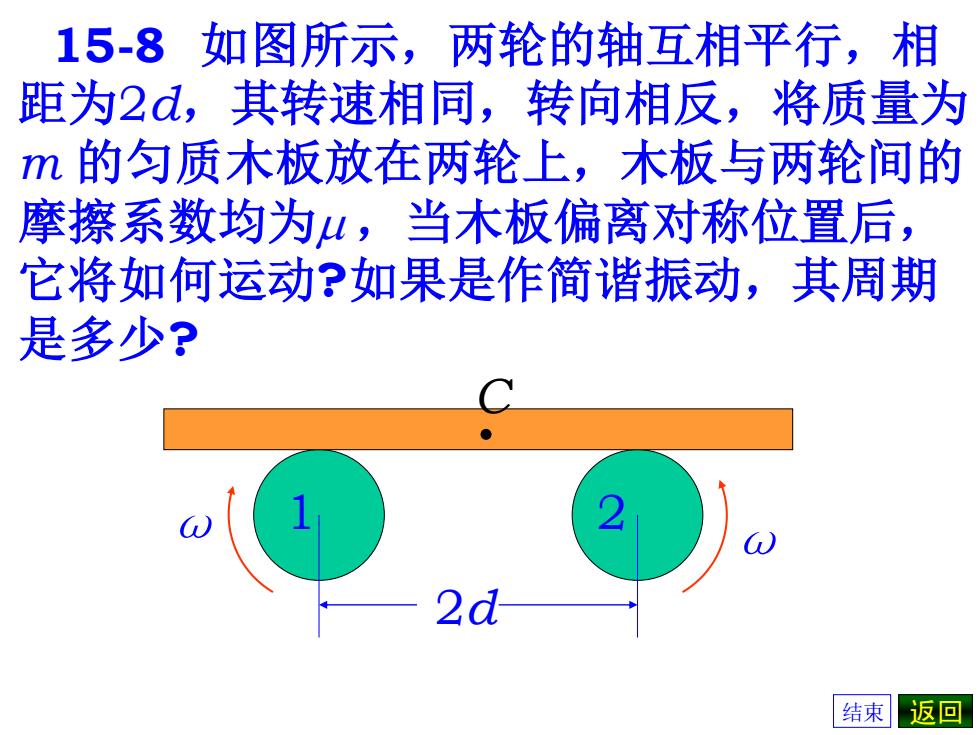
15-8如图所示,两轮的轴互相平行,相 距为2d,其转速相同,转向相反,将质量为 m的匀质木板放在两轮上,木板与两轮间的 摩擦系数均为山,当木板偏离对称位置后, 它将如何运动?如果是作简谐振动,其周期 是多少? 2d 结束返回
15-8 如图所示,两轮的轴互相平行,相 距为2d,其转速相同,转向相反,将质量为 m 的匀质木板放在两轮上,木板与两轮间的 摩擦系数均为m ,当木板偏离对称位置后, 它将如何运动?如果是作简谐振动,其周期 是多少? 2d ω 1 2 C . ω 结束 返回

解: N2 N:+N2 =mg N.(d+x)-Na(d-x)F mg f1=LN f2=uN2 从上述四式解得: N:=mg(d-x) mg(d+x) 2d W2= 2d = umg(d-x) umg(d+x) 2d 2d 结束返回
N1+N2 = mg N1(d +x ) =N2(d x ) f 1 = mN1 + N2 = mg(d x ) 2d mg(d x ) 2d N1 = mg(d x ) 2d f 1 = m + f 2 = mg(d x ) 2d m C . o . N1 N2 f 1 f 2 mg x f 2 = mN2 解: 从上述四式解得: 结束 返回
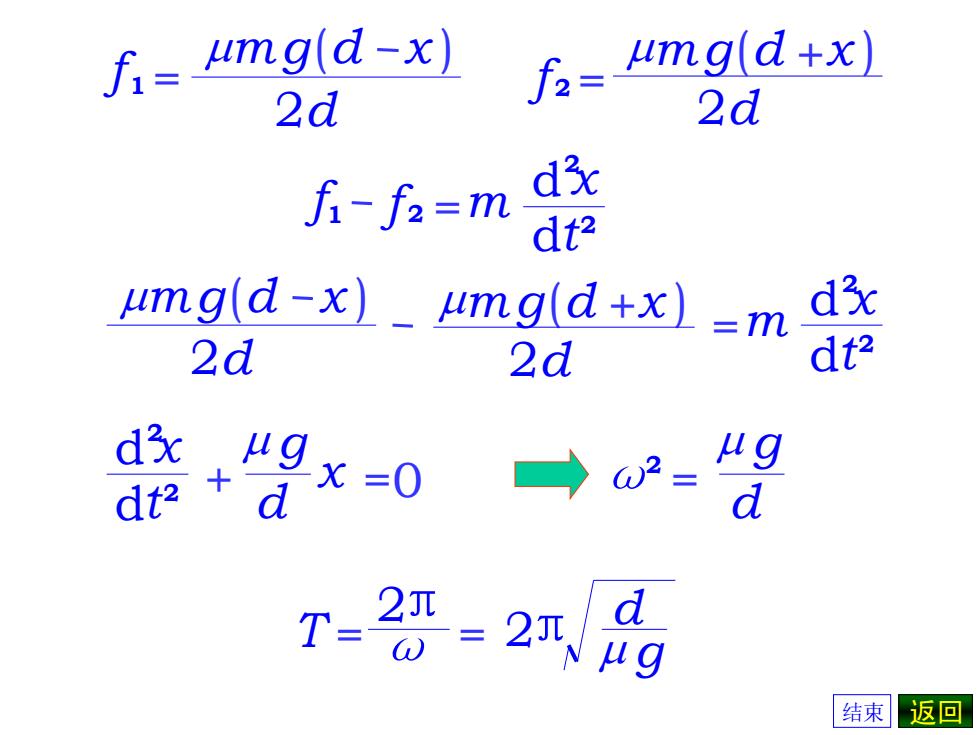
f=umg(d-x) umg(d+x) 2d 2d fi-f2=m dx dt? umg(d-x)umg(d+x)=m d? 2d 2d dt? d dt2 x=0 d →w2= ug d T-2=2 结束返回
mg(d x ) 2d f 1 = m + f 2 = mg(d x ) 2d m d f1 f 2 =m x dt 2 2 d =m x dt 2 2 mg(d x ) mg(d +x ) 2d 2d m m + =0 g d m x d x dt 2 2 T = ω 2π = g d π m 2 ω = 2 g d m 结束 返回
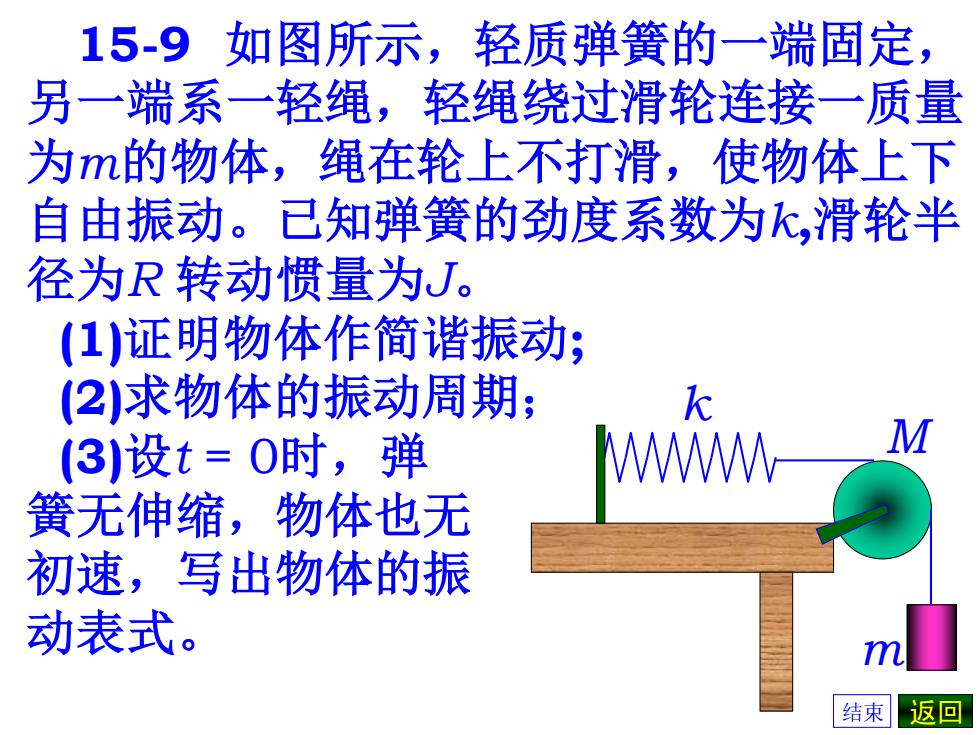
15-9如图所示,轻质弹簧的一端固定, 另一端系一轻绳,轻绳绕过滑轮连接一质量 为m的物体,绳在轮上不打滑,使物体上下 自由振动。已知弹簧的劲度系数为k,滑轮半 径为R转动惯量为U。 (1)证明物体作简谐振动; (2)求物体的振动周期; k 3)设t=0时,弹 WWWW M 簧无伸缩,物体也无 初速,写出物体的振 动表式。 m 结束返回
15-9 如图所示,轻质弹簧的一端固定, 另一端系一轻绳,轻绳绕过滑轮连接一质量 为m的物体,绳在轮上不打滑,使物体上下 自由振动。已知弹簧的劲度系数为k,滑轮半 径为R 转动惯量为J。 (1)证明物体作简谐振动; (2)求物体的振动周期; (3)设t = 0时,弹 簧无伸缩,物体也无 初速,写出物体的振 动表式。 M k m 结束 返回