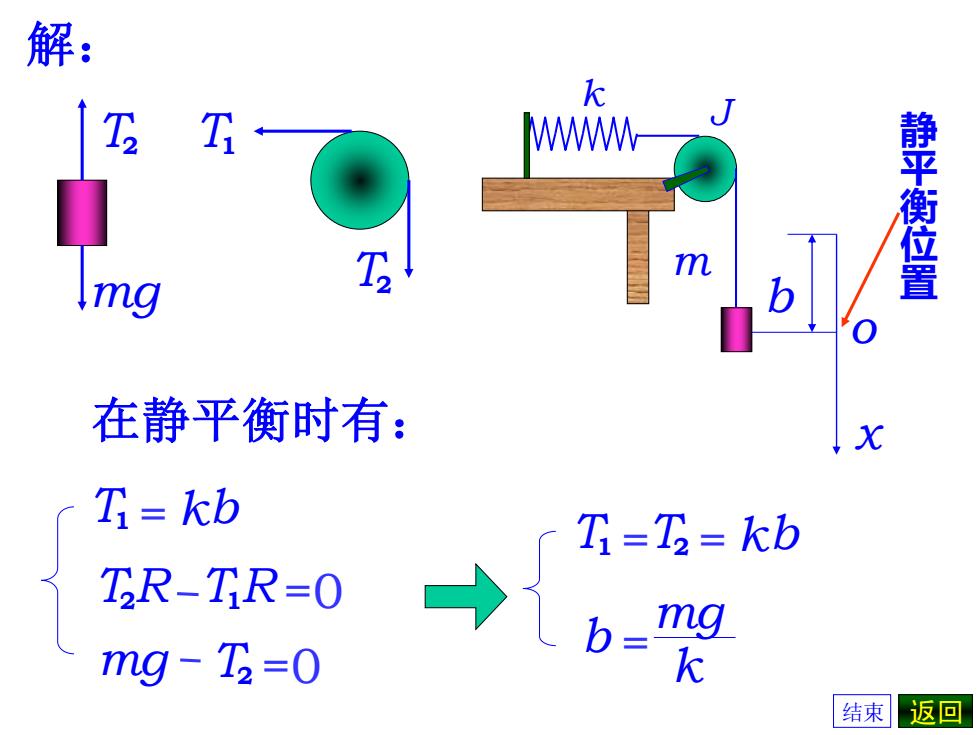
解: k T T WWWM mg T 静平衡位置 在静平衡时有: X T=kb T=T=kb TR-TR-0 g mg T =0 b=" 结束返回
T2 R T1 R =0 T1 = T2 = k b T1 = k b 解: 在静平衡时有:T2 T1 gT2 m J k m xo b 静平衡位置 mg T2 =0 = mg b k 结束 返回
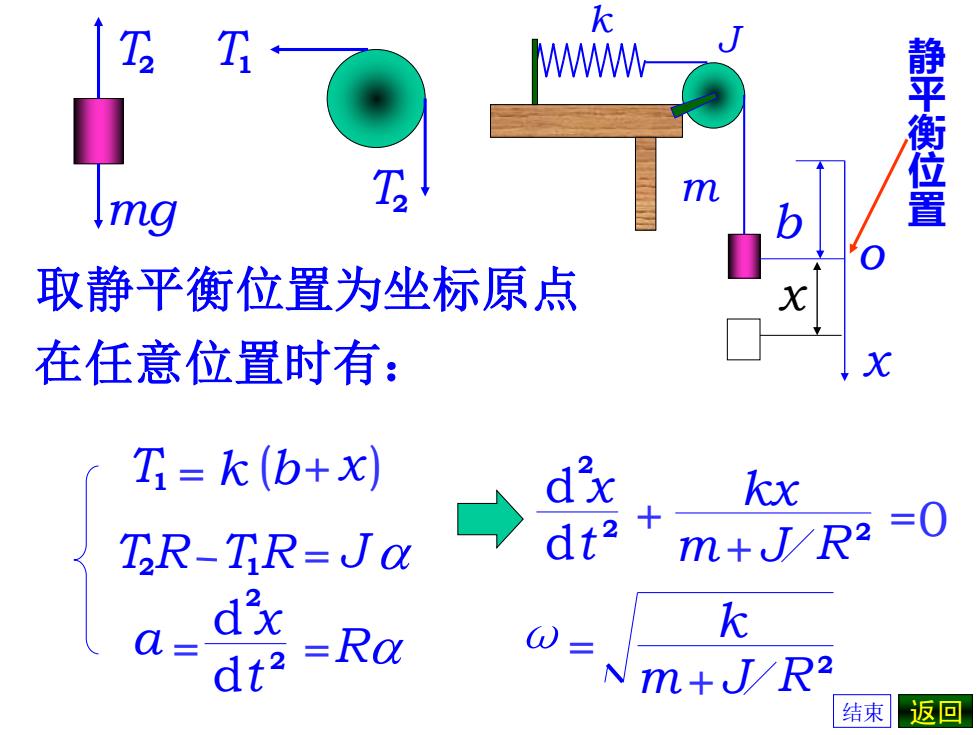
WWWM J 静平衡位置 mg 取静平衡位置为坐标原点 在任意位置时有: X T=k(b+x) d' X TR-TR=Ja → dt 2 m+/R2 =0 a= d'x =Ra k dt2 N m+JR2 结束返回
T1 = k (b+x) T2R T1R = J a 取静平衡位置为坐标原点 J k m x o b 静 平 衡 位 置 x 在任意位置时有: T2 T1 g T2 m a 2 d x = 2 =Ra dt J 2 + + 2 d x 2 =0 dt kx m R ω= J 2 + k m R 结束 返回

)二 K Nm+JR2 T=2 =2、 m+J/R2 ) K 由初始条件: X0=-b=- mg t= )C 0=0 得: P=元 A mg 振动方程为: x= mg coc K k Nm+JR2 t+兀 结束返回
t =0 x = = mg b k 0 A= mg k + J 2 + k m R x = coc mg k t π v0 =0 由初始条件: 得: φ =π 振动方程为: ω= J 2 + k m R + =2π J 2 k m R T = ω 2π 结束 返回
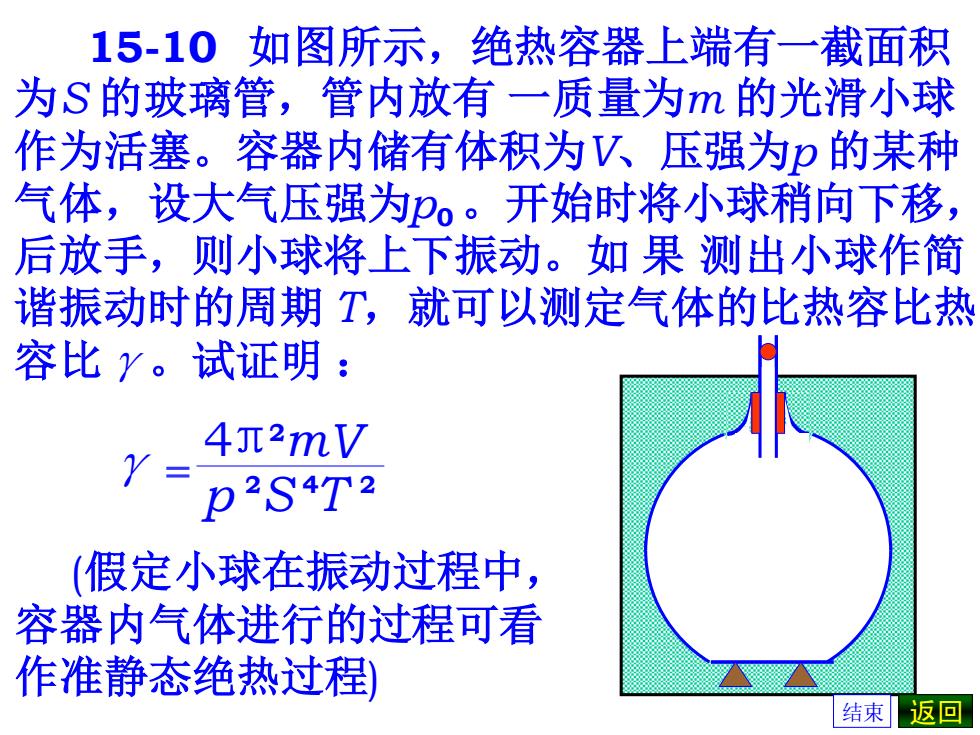
15-10如图所示,绝热容器上端有一截面积 为S的玻璃管,管内放有一质量为m的光滑小球 作为活塞。容器内储有体积为V压强为p的某种 气体,设大气压强为P。开始时将小球稍向下移, 后放手,则小球将上下振动。如果测出小球作简 谐振动时的周期T,就可以测定气体的比热容比热 容比y。试证明: 4元2mV Y= P2S4T2 (假定小球在振动过程中, 容器内气体进行的过程可看 作准静态绝热过程) 结束返回
15-10 如图所示,绝热容器上端有一截面积 为S 的玻璃管,管内放有 一质量为m 的光滑小球 作为活塞。容器内储有体积为V、压强为p 的某种 气体,设大气压强为p0。开始时将小球稍向下移, 后放手,则小球将上下振动。如 果 测出小球作简 谐振动时的周期 T,就可以测定气体的比热容比热 容比γ。试证明 : (假定小球在振动过程中, 容器内气体进行的过程可看 作准静态绝热过程) γ 4πmV p 2 = 2S 4T 2 结束 返回

解:在静平衡时: )0 静平衡位置 poS+mg=pS 任意位置 当小球下降x(任意位置)时: PoS-piS+mg =mdx dt? 由上两式可得到: pS-pS=m dx dt? 设过程是绝热的,所以: PVY=PV V=V-xS pvr=p(V-xS)r 结束返回
解:在静平衡时: 当小球下降 x (任意位置)时: p0 p1 mg x o x 静平衡位置 任意位置 由上两式可得到: 设过程是绝热的,所以: V1 =V xS p0S +mg = pS 1 V γ = p ( )γ p V xS V = γ p V γ p 1 1 d x dt 2 = m 2 pS p1S 0 + d x dt 2 = m 2 p S p1S mg 结束 返回