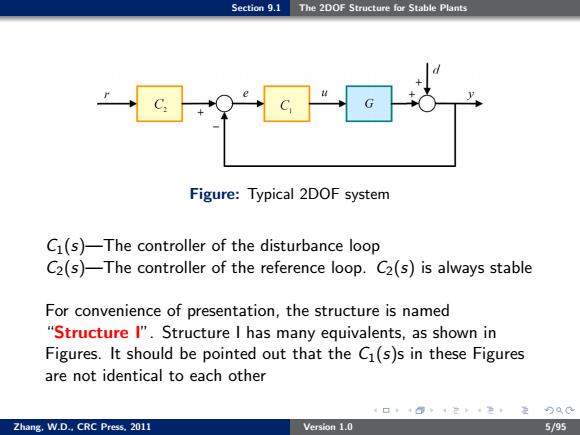
Section 9.1 The 2DOF Structure for Stable Plants Figure:Typical 2DOF system C1(s)-The controller of the disturbance loop C2(s)-The controller of the reference loop.C2(s)is always stable For convenience of presentation,the structure is named "Structure I".Structure I has many equivalents,as shown in Figures.It should be pointed out that the Ci(s)s in these Figures are not identical to each other 4口,+@4定4定, 定9aC Zhang.W.D..CRC Press.2011 Version 1.0 5/95
Section 9.1 The 2DOF Structure for Stable Plants Figure: Typical 2DOF system C1(s)—The controller of the disturbance loop C2(s)—The controller of the reference loop. C2(s) is always stable For convenience of presentation, the structure is named “Structure I”. Structure I has many equivalents, as shown in Figures. It should be pointed out that the C1(s)s in these Figures are not identical to each other Zhang, W.D., CRC Press, 2011 Version 1.0 5/95

Section 9.1 The 2DOF Structure for Stable Plants C Figure:An equivalent of the typical 2DOF system 1 G Figure:Another equivalent of the typical 2DOF system 4口,4日,4注4生,定9QC Zhang,W.D..CRC Press.2011 Version 1.0 6/95
Section 9.1 The 2DOF Structure for Stable Plants Figure: An equivalent of the typical 2DOF system Figure: Another equivalent of the typical 2DOF system Zhang, W.D., CRC Press, 2011 Version 1.0 6/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability:Consider the typical 2DOF system.The input-output relationship is as follows: e(s) C2(s) r(s) 1+G(s)C1(S) y(s) 1 d(s) 1+G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by Ci(s).The analysis for the internal stability is similar to that in a 1DOF system Design:The design of a 2DOF system involves two steps: Design C1(s)for good disturbance response @Design C2(s)for good tracking response 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 7/95
Section 9.1 The 2DOF Structure for Stable Plants Internal stability: Consider the typical 2DOF system. The input-output relationship is as follows: e(s) r(s) = C2(s) 1 + G(s)C1(s) y(s) d(s) = 1 1 + G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by C1(s). The analysis for the internal stability is similar to that in a 1DOF system Design: The design of a 2DOF system involves two steps: 1 Design C1(s) for good disturbance response 2 Design C2(s) for good tracking response Zhang, W.D., CRC Press, 2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants Internal stability:Consider the typical 2DOF system.The input-output relationship is as follows: e(s) C2(s) r(s) 1+G(s)C1(S) y(s) 1 d(s) 1+G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by Ci(s).The analysis for the internal stability is similar to that in a 1DOF system Design:The design of a 2DOF system involves two steps: DDesign C1(s)for good disturbance response 2Design C2(s)for good tracking response 4口:4@4242定90C Zhang,W.D..CRC Press.2011 Version 1.0 7/95
Section 9.1 The 2DOF Structure for Stable Plants Internal stability: Consider the typical 2DOF system. The input-output relationship is as follows: e(s) r(s) = C2(s) 1 + G(s)C1(s) y(s) d(s) = 1 1 + G(s)C1(s) It can be seen that the internal stability of the closed-loop system is only determined by C1(s). The analysis for the internal stability is similar to that in a 1DOF system Design: The design of a 2DOF system involves two steps: 1 Design C1(s) for good disturbance response 2 Design C2(s) for good tracking response Zhang, W.D., CRC Press, 2011 Version 1.0 7/95

Section 9.1 The 2DOF Structure for Stable Plants C1(s):The design of Cl(s)is the same as that for the controller in a 1DOF system C2(s):After C1(s)is designed,the loop consisting of C1(s)and G(s)is viewed as an augmented plant,of which the transfer function is denoted by T(s).The system that consists of C2(s) and T(s)forms the IMC structure with an exact model. Accordingly,C2(s)can be directly designed To illustrate the design procedure,consider the following plant: G(s= T5+1 The system is required to track a step reference,and at the same time to reject the disturbance that is in the form of a ramp at the plant output 4口,+@,4定4定90C Zhang.W.D..CRC Press.2011 Version 1.0 8/95
Section 9.1 The 2DOF Structure for Stable Plants C1(s): The design of C1(s) is the same as that for the controller in a 1DOF system C2(s): After C1(s) is designed, the loop consisting of C1(s) and G(s) is viewed as an augmented plant, of which the transfer function is denoted by T(s). The system that consists of C2(s) and T(s) forms the IMC structure with an exact model. Accordingly, C2(s) can be directly designed To illustrate the design procedure, consider the following plant: G(s) = K τ s + 1 e −θs The system is required to track a step reference, and at the same time to reject the disturbance that is in the form of a ramp at the plant output Zhang, W.D., CRC Press, 2011 Version 1.0 8/95