
模糊方阵A=(a,)m的幂定义为 A=AoA, A=A-A (③)模糊矩阵的转置 定义8设A=(a,)mm,i=l,2.,m广=1,2,.,n,称A=(a)m为A的转 置矩阵,其中a=a, (④)模糊矩阵的元-截矩阵 定义9设A=(an)mm,对任意的1∈[0,1, )令 长 则称A2=(d)mm为模糊矩阵A的2截矩阵。 训令 -kd 则称A=(a)n为模糊矩阵A的2强截矩阵。 显然,对于任意的入∈0,入截矩阵是布尔矩阵。 10.50.20 例7设A=0201108 0.51010.3 则 00.30.81 (1100 1100 1100 1101 4s-0011 A001 0011 0111 下面给出模糊矩阵的一个性质。 -267
-267- 模糊方阵 A = aij m×m ( ) 的幂定义为 A = Ao A 2 , A A A k k o −1 = (3) 模糊矩阵的转置 定义 8 设 A = aij m×n ( ) ,i = 1,2,L,m, j = 1,2,L,n ,称 n m T ji T A a = × ( ) 为 A 的转 置矩阵,其中 ij T ji a = a 。 (4) 模糊矩阵的λ − 截矩阵 定义 9 设 A = aij m×n ( ) ,对任意的λ ∈[0,1], i) 令 ⎪⎩ ⎪ ⎨ ⎧ < ≥ = λ λ λ ij ij ij a a a 0, 1, ( ) 则称 ij m n A a = × ( ) (λ) λ 为模糊矩阵 A 的λ 截矩阵。 ii) 令 ⎪⎩ ⎪ ⎨ ⎧ ≤ > = λ λ λ ij ij ij a a a 0, 1, ( ) 则称 A = aij m×n • ( ) (λ) λ 为模糊矩阵 A 的λ 强截矩阵。 显然,对于任意的λ ∈[0,1],λ 截矩阵是布尔矩阵。 例 7 设 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 0.3 0.8 1 0.2 0.1 1 0.8 0.5 1 0.1 0.3 1 0.5 0.2 0 A ,则 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 0 1 1 0 0 1 1 1 1 0 0 1 1 0 0 A0.5 , ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 1 1 1 0 0 1 1 1 1 0 1 1 1 0 0 A0.3 下面给出模糊矩阵的一个性质

性质设A=(a,)m,i=1,2,.,m,j=l,2,.,n是模糊自反矩阵(对角线上的元 素r,都为1的模糊矩阵),I是n阶单位矩阵,则 I≤R≤R 证:因为A=(a,)m是模糊自反矩阵,即有rm=1,所以I≤R,又 max《as nag)1≤k≤n2raAr=广 即有R≤R2。 §2模糊慎式识别 本节我们假定论域为U,U上的模糊集的全体记为F(U)。 2.1模糊集的贴近度 贴近度是对两个模糊集接近程度的一种度量。 定义10设A,B,C∈F(U),若映射 N:FU)×FU)→[0,1] 满足条件: (1)N(A,B)=N(B,A): (2)N(AA)=1,N(U,①)=0,这里Φ为空集 (3)若ACBEC,则N(A,C)≤N(AB)AN(B,C): 则称N(A,B)为模糊集A与B的贴近度。N称为F(U)上的贴近度函数。 1.海明贴近度 若U={41,山2,.,4n},则 N(4.B)A1-14()-B()I n台 当U为实数域上的闭区间[a,b]时,则有 268
-268- 性质 设 A = aij m×n ( ) ,i = 1,2,L,m, j = 1,2,L,n 是模糊自反矩阵(对角线上的元 素 ij r 都为 1 的模糊矩阵), I 是 n 阶单位矩阵,则 2 I ≤ R ≤ R 证:因为 A = aij m×n ( ) 是模糊自反矩阵,即有 rii= 1,所以 I ≤ R ,又 { ik kj } ii ij ij max (a ∧ a )1 ≤ k ≤ n ≥ r ∧ r = r 即有 2 R ≤ R 。 §2 模糊模式识别 本节我们假定论域为U ,U 上的模糊集的全体记为 F(U)。 2.1 模糊集的贴近度 贴近度是对两个模糊集接近程度的一种度量。 定义 10 设 A, B,C ∈ F(U) ,若映射 N : F(U)× F(U) →[0,1] 满足条件: (1) N(A, B) = N(B, A) ; (2) N(A, A) = 1, N(U,Φ) = 0 ,这里Φ 为空集; (3)若 A ⊆ B ⊆ C ,则 N(A,C) ≤ N(A, B) ∧ N(B,C); 则称 N(A, B) 为模糊集 A 与 B 的贴近度。 N 称为 F(U)上的贴近度函数。 1.海明贴近度 若 { , , , } U = u1 u2 L un ,则 ∑= Δ − − n i A ui B ui n N A B 1 | ( ) ( ) | 1 ( , ) 1 当U 为实数域上的闭区间[a,b]时,则有

M48g-64-u恤 2.欧几里得贴近度 若U={4,42,.,n},则 Mg-②w-ur 当U=a,b时,则有 N(A.B)A1- a(C-aaro 3.黎曼贴近度 若U为实数域,被积函数为黎曼可积,且广义积分收敛,则 NLsy4onBeah B)du 2(A(u)B(u))du N4.+旷amd恤 例8设U=0,100,且 0,0≤x<20 [1,0≤x<40 4x=-20,20≤x<60,B)= 140 96,40≤<0 1,60≤x≤100 0,80≤x≤100 见图1。求黎曼贴近度N,(AB) Ax) 20 4060 图1隶属函数图 -269
-269- A u B u du b a N A B b ∫a − − Δ − | ( ) ( ) | 1 ( , ) 1 2.欧几里得贴近度 若 { , , , } U = u1 u2 L un ,则 1/ 2 1 2 ( ( ) ( )) 1 ( , ) 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ − ∑ − = n i A ui B ui n N A B 当U = [a,b]时,则有 1/ 2 2 ( ( ) ( )) 1 ( , ) 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − Δ − ∫ b a A u B u du b a N A B 3.黎曼贴近度 若U 为实数域,被积函数为黎曼可积,且广义积分收敛,则 ∫ ∫ +∞ −∞ +∞ −∞ ∨ ∧ Δ A u B u du A u B u du N A B ( ( ) ( )) ( ( ) ( )) ( , ) 1 ∫ ∫ ∫ +∞ −∞ +∞ −∞ +∞ −∞ + ∧ Δ A u du B u du A u B u du N A B ( ) ( ) 2 ( ( ) ( )) ( , ) 2 例 8 设U = [0,100],且 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≤ ≤ ≤ < − ≤ < = 1, 60 100 , 20 60 40 20 0, 0 20 ( ) x x x x A x , ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≤ ≤ ≤ < − ≤ < = 0, 80 100 , 40 80 40 80 1, 0 40 ( ) x x x x B x 见图 1。求黎曼贴近度 ( , ) N1 A B 。 图 1 隶属函数图
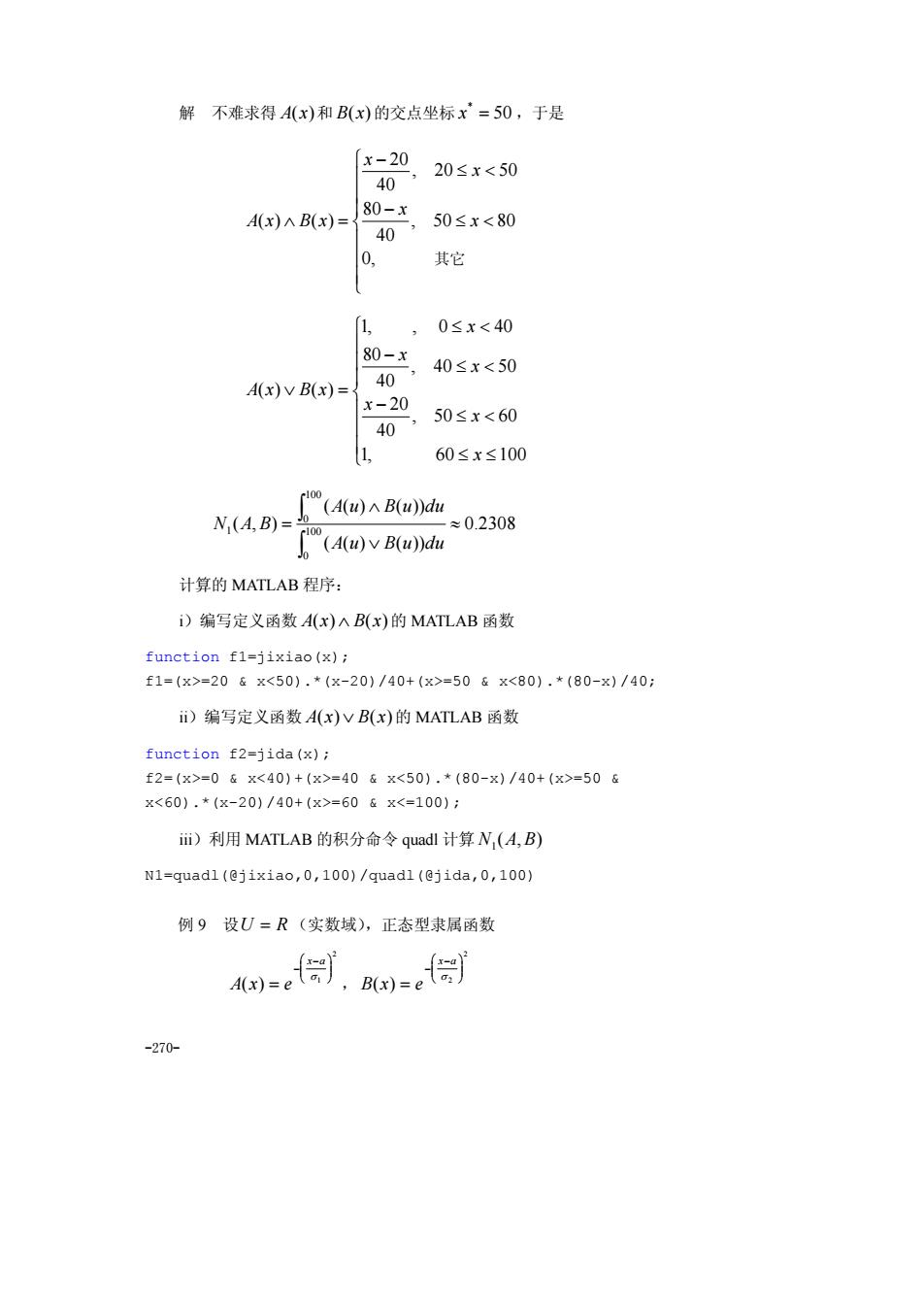
解不难求得A(x)和B(x)的交点坐标x'=50,于是 [x-20 40 ,20≤x<50 80-x A(X)A B(x)= 40 ,50≤x<80 0, 其它 0≤x<40 80-x 40≤x<50 A(x)vB(x)= 40 x-20 40 ,50≤x<60 60≤x≤100 [(A(u)B(u)du N(4.B)= ≈0.2308 (A(u)B(u))du 计算的MATLAB程序: i)编写定义函数A(x)AB(x)的MATLAB函数 function f1-jixiao(x); f1=(x>=20x<50).*(x-20)/40+(x>=50&x<80).*(80-x)/40: i)编写定义函数4A(x)VB(x)的MATLAB函数 function f2-jida(x); f2=(x>=0&x<40)+(x>=40&x<50).*(80-x)/40+(x>=50& X<60).*(X-20)/40+(x>=60&X<=100): i)利用MATLAB的积分命令quadl计算N,(A,B) N1-quadl(@jixiao,0,100)/quadl(@jida,0,100) 例9设U=R(实数域),正态型隶属函数 270-
-270- 解 不难求得 A(x)和 B(x)的交点坐标 50 * x = ,于是 ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ≤ < − ≤ < − ∧ = 0, 其它 , 50 80 40 80 , 20 50 40 20 ( ) ( ) x x x x A x B x ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ≤ ≤ ≤ < − ≤ < − ≤ < ∨ = 1, 60 100 , 50 60 40 20 , 40 50 40 80 1, , 0 40 ( ) ( ) x x x x x x A x B x 0.2308 ( ( ) ( )) ( ( ) ( )) ( , ) 100 0 100 0 1 ≈ ∨ ∧ = ∫ ∫ A u B u du A u B u du N A B 计算的 MATLAB 程序: i)编写定义函数 A(x) ∧ B(x)的 MATLAB 函数 function f1=jixiao(x); f1=(x>=20 & x<50).*(x-20)/40+(x>=50 & x<80).*(80-x)/40; ii)编写定义函数 A(x)∨ B(x)的 MATLAB 函数 function f2=jida(x); f2=(x>=0 & x<40)+(x>=40 & x<50).*(80-x)/40+(x>=50 & x<60).*(x-20)/40+(x>=60 & x<=100); iii)利用 MATLAB 的积分命令 quadl 计算 ( , ) N1 A B N1=quadl(@jixiao,0,100)/quadl(@jida,0,100) 例 9 设U = R (实数域),正态型隶属函数 2 1 ( ) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = σ x a A x e , 2 2 ( ) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − = σ x a B x e

求当o,≤02时,N(A,B)(见图2) xO d x'a 图2隶属函数图 解当o,≤o2,x∈R,A(x)≤B(x) 根据黎曼贴近度,有 N(A,B)= [A(a B(x)dx 24(xydx 2o. N2(A,B)= s+Bxyo+o: 2.2格贴近度 定义10设AB∈FU),称 A⊙B=Y(A0)AB(u) 为模糊集A,B的内积。 内积的对偶运算为外积。 定义11设AB∈F(U),称 A®B=A(A(u)vB(u) 为模糊集A,B的外积。 如果在闭区间0,】上定义“余”运算:a∈0,小,a‘-1-a,那么有性质1 性质1(A⑧B)°=A⊙B,(A⊙B)=A⑧B 对A∈F(U),令 -271
-271- 求当σ 1 ≤ σ 2 时, N(A, B) (见图 2) 图 2 隶属函数图 解 当σ1 ≤ σ 2 ,∀x ∈ R , A(x) ≤ B(x) 根据黎曼贴近度,有 2 1 1 ( ) ( ) ( , ) σ σ = = ∫ ∫ +∞ −∞ +∞ −∞ B x dx A x dx N A B 1 2 1 2 2 ( ) ( ) 2 ( ) ( , ) σ σ σ + = + = ∫ ∫ ∫ +∞ −∞ +∞ −∞ +∞ −∞ A x dx B x dx A x dx N A B 2.2 格贴近度 定义 10 设 A, B ∈ F(U) ,称 A ⊙ B (A(u) B(u)) u U = ∨ ∧ ∈ 为模糊集 A, B 的内积。 内积的对偶运算为外积。 定义 11 设 A, B ∈ F(U) ,称 A B (A(u) B(u)) u U ⊗ = ∧ ∨ ∈ 为模糊集 A, B 的外积。 如果在闭区间[0,1]上定义“余”运算:∀α ∈[0,1],α = 1−α c ,那么有性质 1 性质 1 c c (A⊗ B) = A ⊙ c B ,(A ⊙ c c c B) = A ⊗ B 。 对 A∈ F(U) ,令