
指派方法是一种主观的方法,它主要依据人们的实践经验来确定某些模糊集求属函 数的一种方法。 如果模糊集定义在实数域R上,则模糊集的隶屈函数称为模糊分布。所谓指派方 法就是根据问题的性质主观地选用某些形式地模糊分布,再根据实际测量数据确定其中 所包含地参数,常用的模糊分布如表1所示。 实际中,根据问题对研究对象的描述来选择适当的模糊分布: ①偏小型模糊分布一般适合于描述像“小,少,浅,淡,冷,疏,青年”等偏小 的程度的模糊现象。 ②偏大型模糊分布一般适合于描述像“大,多,深,浓,热,密,老年”等偏大 的程度的模糊现象。 ③中间型模糊分布一般适合于描述像“中,适中,不太多,不太少,不太深,不 太浓,暖和,中年”等处于中间状态的模糊现象。 但是,表1给出的隶属函数都是近似的,应用时需要对实际问题进行分析,逐步修 改进行完善,最后得到近似程度更好的隶属函数。 (3)其它方法 在实际应用中,用来确定模糊集的隶属函数的方法示多种多样的,主要根据问题的 实际意义来确定。譬如,在经济管理、社会管理中,可以借助于已有的“客观尺度”作 为模糊集的隶属度。下面举例说明。 如果设论域X表示机器设备,在X上定义模糊集A=“设备完好”,则可以用“设 备完好率”作为A的隶属度。如果X表示产品,在X上定义模糊集A=“质量稳定”, 则可以用产品的“正品率”作为A的隶属度。如果X表示家庭,在X上定义模糊集A =“家庭贫困”,则可以用“Egl系数=食品消费/总消费”作为A的求属度。 另外,对于有些模糊集而言,直接给出隶属度有时是很困难的,但可以利用所谓的 “二元对比排序法”来确定,即首先通过两两比较确定两个元素相应隶属度的大小排出 顺序,然后用数学方法加工处理得到所需的隶属函数。 -262
-262- 指派方法是一种主观的方法,它主要依据人们的实践经验来确定某些模糊集隶属函 数的一种方法。 如果模糊集定义在实数域 R 上,则模糊集的隶属函数称为模糊分布。所谓指派方 法就是根据问题的性质主观地选用某些形式地模糊分布,再根据实际测量数据确定其中 所包含地参数,常用的模糊分布如表 1 所示。 实际中,根据问题对研究对象的描述来选择适当的模糊分布: ① 偏小型模糊分布一般适合于描述像“小,少,浅,淡,冷,疏,青年”等偏小 的程度的模糊现象。 ② 偏大型模糊分布一般适合于描述像“大,多,深,浓,热,密,老年”等偏大 的程度的模糊现象。 ③ 中间型模糊分布一般适合于描述像“中,适中,不太多,不太少,不太深,不 太浓,暖和,中年”等处于中间状态的模糊现象。 但是,表 1 给出的隶属函数都是近似的,应用时需要对实际问题进行分析,逐步修 改进行完善,最后得到近似程度更好的隶属函数。 (3)其它方法 在实际应用中,用来确定模糊集的隶属函数的方法示多种多样的,主要根据问题的 实际意义来确定。譬如,在经济管理、社会管理中,可以借助于已有的“客观尺度”作 为模糊集的隶属度。下面举例说明。 如果设论域 X 表示机器设备,在 X 上定义模糊集 A =“设备完好”,则可以用“设 备完好率”作为 A 的隶属度。如果 X 表示产品,在 X 上定义模糊集 A =“质量稳定”, 则可以用产品的“正品率”作为 A 的隶属度。如果 X 表示家庭,在 X 上定义模糊集 A =“家庭贫困”,则可以用“Engel 系数=食品消费/总消费”作为 A 的隶属度。 另外,对于有些模糊集而言,直接给出隶属度有时是很困难的,但可以利用所谓的 “二元对比排序法”来确定,即首先通过两两比较确定两个元素相应隶属度的大小排出 顺序,然后用数学方法加工处理得到所需的隶属函数

表1常用的模糊分布 型 偏小型 中间型 偏大型 矩 asxsb 0,x<a或x>b -6a [x-a x≤a b-a' asxsb 0, x <a b-x a≤x≤b b≤x≤c = a≤x≤b 型 b-a d-x d-c' csxsd 10. x>b x>6 x<a.xzd x≤a -a,a≤x≤b b-a 0, x<a b≤x≤c 抛物 10, x>b d-xy.csxsd 型 d-c x>b x<a,x2d (ems-a)x<a 1 r≤a 0, x<a 型 asxsb e-k(s-a),x>b =1-cn-,x2d 公 x≤a x≤a “= 型 4,=m:9} u-h-} x≤a 0. x≤a 1 1 =+a(x-ay 1 西型 (l+a(x-ay.x>a (I+ax-ay.x>a (a>0,B为正偶数) (a>0,B>0) (a>0,B>0) 1.3模糊关系、模糊矩阵 -263
-263- 表 1 常用的模糊分布 类 型 偏小型 中间型 偏大型 矩 阵 型 ⎩ ⎨ ⎧ > ≤ = x a x a A 0, 1, μ ⎩ ⎨ ⎧ < > ≤ ≤ = x a x b a x b A 0, 或 1, μ ⎩ ⎨ ⎧ < ≥ = x a x a A 0, 1, μ 梯 形 型 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ > ≤ ≤ − − ≤ = x b a x b b a b x x a A 0, , 1, μ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ < ≥ ≤ ≤ − − ≤ ≤ ≤ ≤ − − = x a x d c x d d c d x b x c a x b b a x a A 0, , , 1, , μ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ > ≤ ≤ − − < = x b a x b b a x a x a A 1, , 0, μ k 次 抛 物 型 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ > ≤ ≤ − − ≤ = x b a x b b a b x x a k A 0, ( ) , 1, μ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ < ≥ ≤ ≤ − − ≤ ≤ ≤ ≤ − − = x a x d c x d d c d x b x c a x b b a x a k k A 0, , ( ) , 1, ( ) , μ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ > ≤ ≤ − − < = x b a x b b a x a x a k A 1, ( ) , 0, μ Γ 型 ⎩ ⎨ ⎧ > ≤ = − − e x a x a A k x a , 1, ( ) μ ⎪ ⎩ ⎪ ⎨ ⎧ > ≤ ≤ < = − − − e x b a x b e x a k x a k x a A , 1, , ( ) ( ) μ ⎩ ⎨ ⎧ − ≥ < = − − e x a x a A k x a 1 , 0, ( ) μ 正 态 型 ⎪ ⎩ ⎪ ⎨ ⎧ > ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ≤ = x a x a x a A exp , 1, 2 σ μ ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − 2 exp σ μ x a A ⎪ ⎩ ⎪ ⎨ ⎧ > ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − ≤ = x a x a x a A 1 exp , 0, 2 σ μ 柯 西 型 ⎪ ⎩ ⎪ ⎨ ⎧ > + − ≤ = x a x a x a A , 1 ( ) 1 1, β α μ (α > 0, β > 0) β α μ 1 ( ) 1 x a A + − = (α > 0, β 为正偶数) ⎪ ⎩ ⎪ ⎨ ⎧ > + − ≤ = − x a x a x a A , 1 ( ) 1 0, β α μ (α > 0, β > 0) 1.3 模糊关系、模糊矩阵

13.1基本概念 定义4设论域U,V,乘积空间上U×V={(u,v)!∈U,v∈仍上的一个模糊 子集R为从从集合U到集合V的模糊关系。如果模糊关系R的隶屈函数为 g:UxV→[0,(x,y)→4(x,y) 则称隶属度4(x,)为(x,y)关于模糊关系R的相关程度。 这是二元模糊关系的数学定义,多元模糊关系也可以类似定义。 设U={,x2,.,xn,V=y,2,.,yn},R为从从U到V的模糊关系,其 隶属函数为4R(xy),对任意的(x,y,)∈U×V有4(:,y,)=r,∈0, i=1,2,.,mj=1,2,.,n,记R=()m则R就是所谓的模糊矩阵。下面给出 般的定义。 定义5设矩阵R=(化)m’且r,∈[0,则,i=l2,m,j=12,.,n,则R称 为模糊矩阵 特别地,如果r,∈{0,1},i=1,2.,mj=1,2,.,n,则称R为布尔Bol)矩阵。 当模糊方阵R=(亿,)的对角线上的元素r,都为1时,称R为模糊自反矩阵, 当m=1或者n=1时,相应地模糊矩阵为R=(,.,)或者 R=(,h,.,)了,则分别称为模糊行向量和模糊列向量。 例4设评定科研成果等级的指标集为U=(,x2,x),x表示为科研成果发 明或创造、革新的程度,X,表示安全性能,x表示经济效益,x4表示推广前景,x,表 示成熟性:V表示定性评价的评语论域厂=(少,2,少,),乃,分别表示很 好、较好、一般、不好。通过专家评审打分,按下表给出U×上每个有序对(x,y,)指 定的隶属度。 -264-
-264- 1.3.1 基本概念 定义 4 设论域U ,V ,乘积空间上U ×V = {(u, v) u ∈U, v ∈V}上的一个模糊 子集 R 为从从集合U 到集合V 的模糊关系。如果模糊关系 R 的隶属函数为 μ R :U ×V → [0,1], (x, y) a (x, y) μ R 则称隶属度 (x, y) μ R 为(x, y)关于模糊关系 R 的相关程度。 这是二元模糊关系的数学定义,多元模糊关系也可以类似定义。 设 { }m U x , x , , x = 1 2 L ,V = {y1 , y2 ,L, yn }, R 为从从U 到V 的模糊关系,其 隶属函数为 (x, y) μ R ,对任意的 ( , ) i j x y ∈ U ×V 有 ( , ) = ∈[0,1] R i j ij μ x y r , i = 1,2,L,m, j = 1,2,L,n ,记 ij m n R r = × ( ) ,则 R 就是所谓的模糊矩阵。下面给出一 般的定义。 定义 5 设矩阵 ij m n R r = × ( ) ,且 ∈[0,1] ij r ,i = 1,2,L,m, j = 1,2,L,n ,则 R 称 为模糊矩阵。 特别地,如果 ∈{0,1} ij r ,i = 1,2,L,m, j = 1,2,L,n ,则称 R 为布尔(Bool)矩阵。 当模糊方阵 ij n n R r = × ( ) 的对角线上的元素 ij r 都为 1 时,称 R 为模糊自反矩阵。 当 m = 1 或 者 n = 1 时,相应地模糊矩阵为 ( , , , ) 1 2 n R = r r L r 或 者 T n R (r ,r , ,r ) = 1 2 L ,则分别称为模糊行向量和模糊列向量。 例 4 设评定科研成果等级的指标集为 ( , , , ) 1 2 5 U = x x L x , 1 x 表示为科研成果发 明或创造、革新的程度, 2 x 表示安全性能, 3 x 表示经济效益, 4 x 表示推广前景, 5 x 表 示成熟性;V 表示定性评价的评语论域 ( , , , ) 1 2 3 4 V = y y y y , 1 2 3 4 y , y , y , y 分别表示很 好、较好、一般、不好。通过专家评审打分,按下表给出U ×V 上每个有序对( , ) i i x y 指 定的隶属度
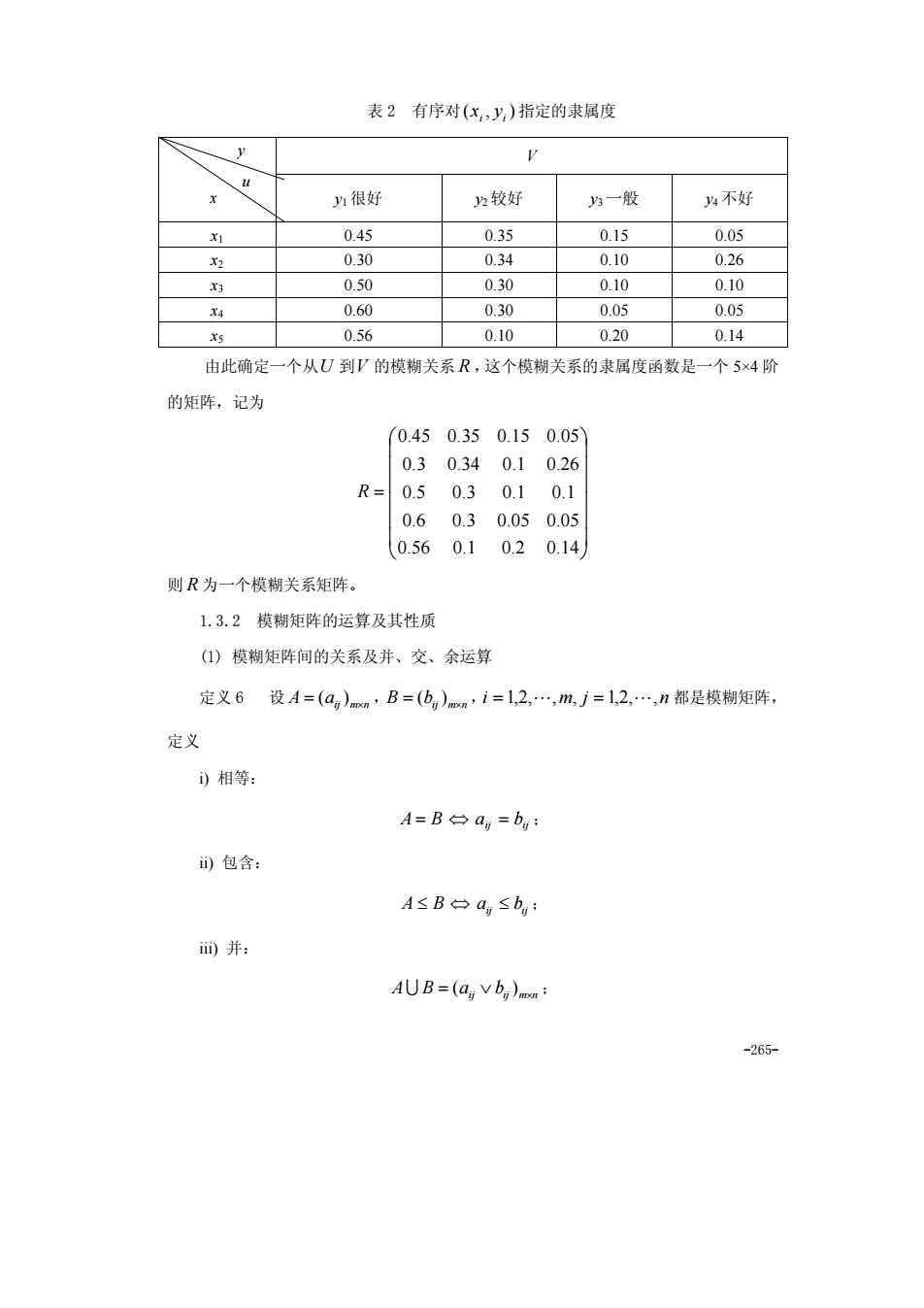
表2有序对(x,y,)指定的隶属度 ”很好 2较好 为一般 4不好 0.45 035 0.15 005 030 0.34 0.10 026 3 050 0.30 0.10 0.10 Xa 0.60 0.30 0.05 0.05 0.56 0.10 0.20 0.14 由此确定一个从U到V的模糊关系R,这个模糊关系的隶属度函数是一个5×4阶 的矩阵,记为 (0.450.350.150.05 0.30.340.10.26 R=0.50.30.10.1 0.60.30.050.05 0.560.10.20.14 则R为一个模糊关系矩阵。 1.3.2模糊矩阵的运算及其性质 (1)模糊矩阵间的关系及并、交、余运算 定义6设A=(a)m,B=(b)m,i=1,2,.,m,j=1,2,.,n都是模糊矩阵, 定义 )相等: A=B台ag=b, 的包含: A≤Ba,≤b, 并: AUB=(avb,)mm: -265
-265- 表 2 有序对( , ) i i x y 指定的隶属度 V y1 很好 y2 较好 y3 一般 y4 不好 x1 0.45 0.35 0.15 0.05 x2 0.30 0.34 0.10 0.26 x3 0.50 0.30 0.10 0.10 x4 0.60 0.30 0.05 0.05 x5 0.56 0.10 0.20 0.14 由此确定一个从U 到V 的模糊关系 R ,这个模糊关系的隶属度函数是一个 5×4 阶 的矩阵,记为 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 0.56 0.1 0.2 0.14 0.6 0.3 0.05 0.05 0.5 0.3 0.1 0.1 0.3 0.34 0.1 0.26 0.45 0.35 0.15 0.05 R 则 R 为一个模糊关系矩阵。 1.3.2 模糊矩阵的运算及其性质 (1) 模糊矩阵间的关系及并、交、余运算 定义 6 设 A = aij m×n ( ) ,B = bij m×n ( ) ,i = 1,2,L,m, j = 1,2,L,n 都是模糊矩阵, 定义 i) 相等: A = B ⇔ aij = bij ; ii) 包含: A ≤ B ⇔ aij ≤ bij ; iii) 并: A B = aij ∨ bij m×n U ( ) ; y u x

v)交: AnB=(dybe) v)余: Ac =(1-ag)mon 设408时-: us-48gns-8g)4-8阁 (2)模糊矩阵的合成 定义7设A=(ak)’B=(亿)m,称模糊矩阵 AoB=(Cy) 为A与B的合成,其中 cy=max《au by巾sk≤s} 例6设A=04070) (10.7 ,B=0.40.6,则 10.80.5 00.3 0.70.70.5 a-0489 ,BoA=0.60.60.5 0.30.30.3 两模糊矩阵合成的MATLAB函数如下: function ab=synt(a,b); m=size(a,1);n=size(b,2) for i-1:m for j=1:n ab(i,j)-max (min([a(i,::b(:j)])); end end -266-
-266- iv) 交: A B = aij ∧ bij m×n I ( ) v) 余: ij m n C A a = − × (1 ) 例 5 设 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 0.3 0.5 1 0.1 A , ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 0.4 0.9 0.7 0 B ,则 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 0.4 0.9 1 0.1 AU B , ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 0.3 0.5 0.7 0 AI B , = C A ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ 0.7 0.5 0 0.9 (2) 模糊矩阵的合成 定义 7 设 A = aik m×s ( ) , B = bkj s×n ( ) ,称模糊矩阵 ij m n A B c = × o ( ) 为 A 与 B 的合成,其中 cij = max{(aik ∧ bkj )1 ≤ k ≤ s} 例 6 设 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 1 0.8 0.5 0.4 0.7 0 A , ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 0.3 0.4 0.6 1 0.7 B ,则 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = 1 0.7 0.4 0.6 Ao B , ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = 0.3 0.3 0.3 0.6 0.6 0.5 0.7 0.7 0.5 B o A 两模糊矩阵合成的 MATLAB 函数如下: function ab=synt(a,b); m=size(a,1);n=size(b,2); for i=1:m for j=1:n ab(i,j)=max(min([a(i,:);b(:,j)'])); end end