
c*(1) r0r*(2 G(s) 404 G,(s)c() 一G() (2)串联环节间无采样器时 如图7一3(b)所示,由于环节间没有采样器,因而G,(S)环节输入的信号不 是脉冲序列,而是连续函数,所以不能象图7-3(a)那样求G2()=C(e)/U1(e), 而应先把G(s)、G,(s)进行串联运算求出等效环节G,(s)G,(s),则G,(s)G,(s) 的:变换才是R()、C()之间的脉冲传递函数。即 Ge)-cQ-zG.wc.-G.c,) (7-9) R() 式中G,G2(:)表示G(S)G,(s)乘积经采样后的z变换。显然 ZG(s)G,(s)=GG,()G)G,() (7-10) 即各环节传递函数乘积的z变换,不等于各环节传递函数?变换的乘积。 c*) r(t)/r*() 41(1) G(s) G2(s) c() G() 由此可知,两个串联环节间无采样器隔开时,则等效脉冲传递函数等于两个环 节传递函数乘积经采样后的z变换。同理,此结论也使用于多个环节串联而无采样 器隔开的情况,即有 G()=ZG(s)G2(s)G(s)=GG2G() (7-11) 如果串联的多个环节中存在上述两种情况,则分段按上述原则处理。 如果把离散后的传递函数或变量记为G*(),则可以把上述两种情况简单归纳 110
110 (2) 串联环节间无采样器时 如图 7-3(b)所示,由于环节间没有采样器,因而 ( ) 2 G s 环节输入的信号不 是脉冲序列,而是连续函数,所以不能象图 7-3(a)那样求 ( ) ( ) ( ) 2 1 G z = C z U z , 而应先把 ( ) 1 G s 、 ( ) 2 G s 进行串联运算求出等效环节 ( ) ( ) 1 2 G s G s ,则 ( ) ( ) 1 2 G s G s 的 z 变换才是 R(z)、C(z) 之间的脉冲传递函数。即 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 Z G s G s G G z R z C z G z = = = (7-9) 式中 ( ) 1 2 G G z 表示 ( ) ( ) 1 2 G s G s 乘积经采样后的 z 变换。显然 ( ) ( ) ( ) ( ) ( ) 1 2 1 2 1 2 Z G s G s = G G z G z G z (7-10) 即各环节传递函数乘积的 z 变换,不等于各环节传递函数 z 变换的乘积。 由此可知,两个串联环节间无采样器隔开时,则等效脉冲传递函数等于两个环 节传递函数乘积经采样后的 z 变换。同理,此结论也使用于多个环节串联而无采样 器隔开的情况,即有 ( ) ( ) ( ) ( ) ( ) 1 2 1 2 G z Z G s G s G s G G G z = n = n (7-11) 如果串联的多个环节中存在上述两种情况,则分段按上述原则处理。 如果把离散后的传递函数或变量记为 G * (s) ,则可以把上述两种情况简单归纳 ( ) 1 G s ( ) 2 G s *( ) 1 ( ) u t 1 u t c(t) c * (t) ( ) 1 G z ( ) 2 G z r(t) r * (t) ( ) 1 G s ( ) 2 G s ( ) 1 u t c(t) c * (t) G (z) r(t) r * (t)
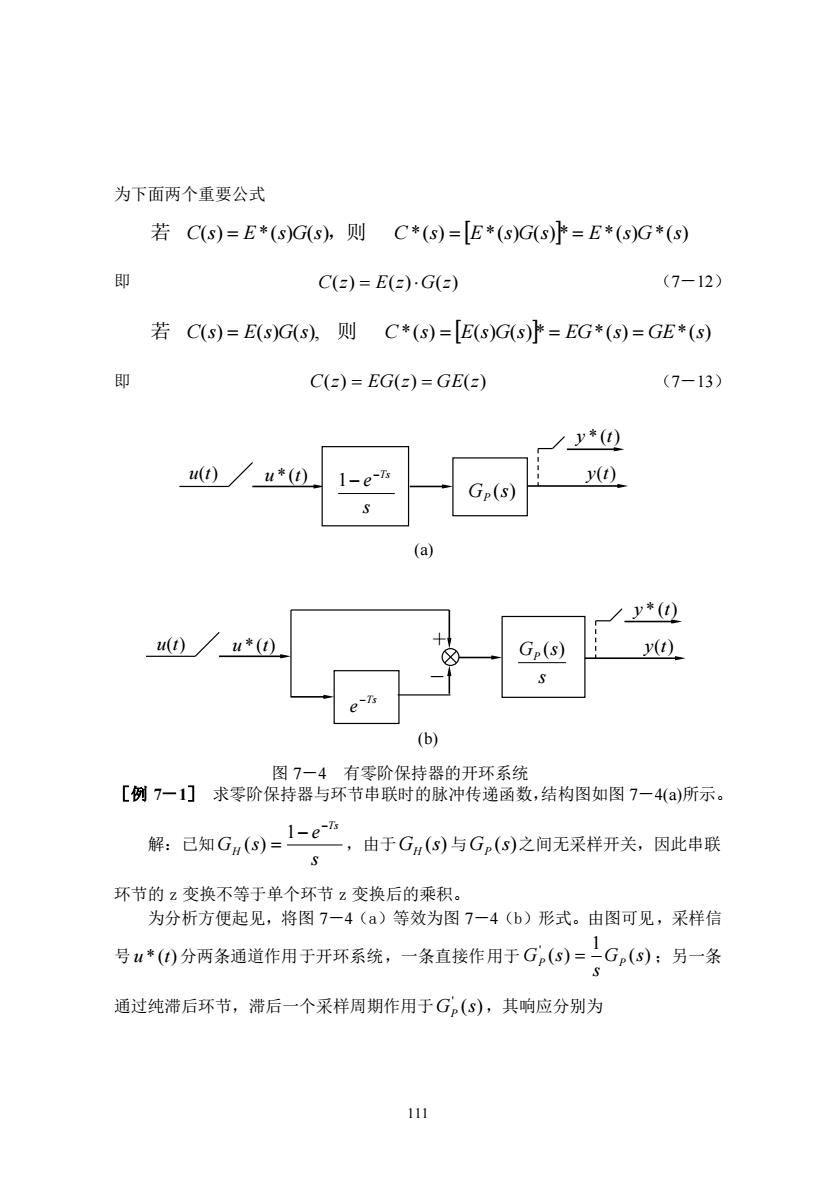
为下面两个重要公式 C(s)=E*(s)G(s),C*(s)=E*(s)G(s)=E*(s)G*(s) C()=E()G() (7-12) C(s)=E(s)G(s).C*(s)=E(s)G(s)=EG*(s)=GE*(s) C()=EG()=GE() (7-13) /y*@ 1-e- y(t) Gp(s) (a) /y*() G(s) y(t) e-k (b) 图7一4有零阶保持器的开环系统 [例7一1]求零阶保持器与环节串联时的脉冲传递函数,结构图如图7一4()所示。 解:已知Gn)=1-e” ,由于G(s)与G。(s)之间无采样开关,因此串联 环节的z变换不等于单个环节z变换后的乘积。 为分析方便起见,将图7-4(a)等效为图7-4(b)形式。由图可见,采样信 号1*(0分两条通道作用于开环系统,一条直接作用于G,(⊙)=上G,(S):另一条 通过纯滞后环节,滞后一个采样周期作用于G(),其响应分别为 111
111 为下面两个重要公式 若 C(s) = E*(s)G(s),则 C*(s) = E*(s)G(s)* = E*(s)G*(s) 即 C(z) = E(z)G(z) (7-12) 若 C(s) = E(s)G(s), 则 C*(s) = E(s)G(s)* = EG*(s) = GE*(s) 即 C(z) = EG(z) = GE(z) (7-13) [例 7-1] 求零阶保持器与环节串联时的脉冲传递函数,结构图如图 7-4(a)所示。 解:已知 s e G s Ts H − − = 1 ( ) ,由于 G (s) H 与 G (s) P 之间无采样开关,因此串联 环节的 z 变换不等于单个环节 z 变换后的乘积。 为分析方便起见,将图 7-4(a)等效为图 7-4(b)形式。由图可见,采样信 号 u *(t) 分两条通道作用于开环系统,一条直接作用于 ( ) 1 ( ) ' G s s G s P = P ;另一条 通过纯滞后环节,滞后一个采样周期作用于 ( ) ' G s P ,其响应分别为 s e −Ts 1− G (s) P u(t) u *(t) y(t) y * (t) (a) Ts e − s G s P ( ) y(t) y * (t) u(t) u *(t) + - (b) 图 7-4 有零阶保持器的开环系统