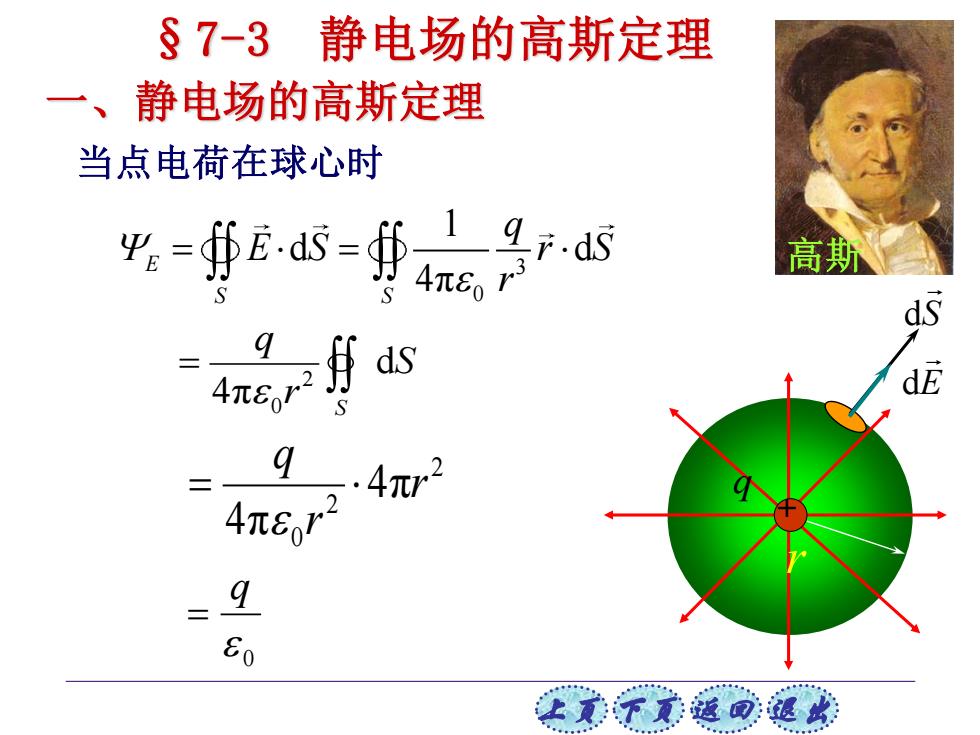
§7-3静电场的高斯定理 一、静电场的高斯定理 当点电荷在球心时 年Ed∯是r 高斯 dE 4r2 4π6r1 Eo 让美子觉返同速
上页 下页 返回 退出 高斯 + q 一、静电场的高斯定理 3 0 1 d d 4π E S S q E S r S r = = S r q S d 4π 2 0 = 2 2 0 4π 4π r r q = 当点电荷在球心时 r §7-3 静电场的高斯定理 0 q = S d E d
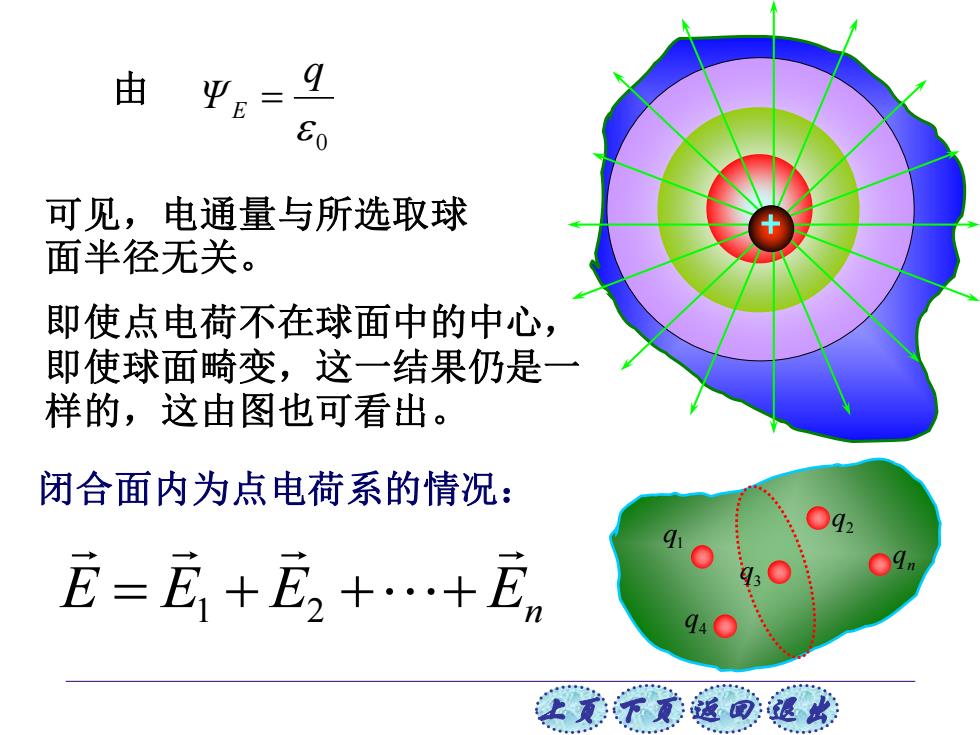
由 平E 9 60 可见,电通量与所选取球 面半径无关。 即使点电荷不在球面中的中心, 即使球面畸变,这一结果仍是一 样的,这由图也可看出。 闭合面内为点电荷系的情况: ○q2 E=E+E,+.+E 09m 94○ 上美齐京返可退
上页 下页 返回 退出 可见,电通量与所选取球 面半径无关。 由 闭合面内为点电荷系的情况: q1 q3 4 q 2 q n q E E E En = 1 + 2 + + 即使点电荷不在球面中的中心, 即使球面畸变,这一结果仍是一 样的,这由图也可看出。 0 q ΨE =
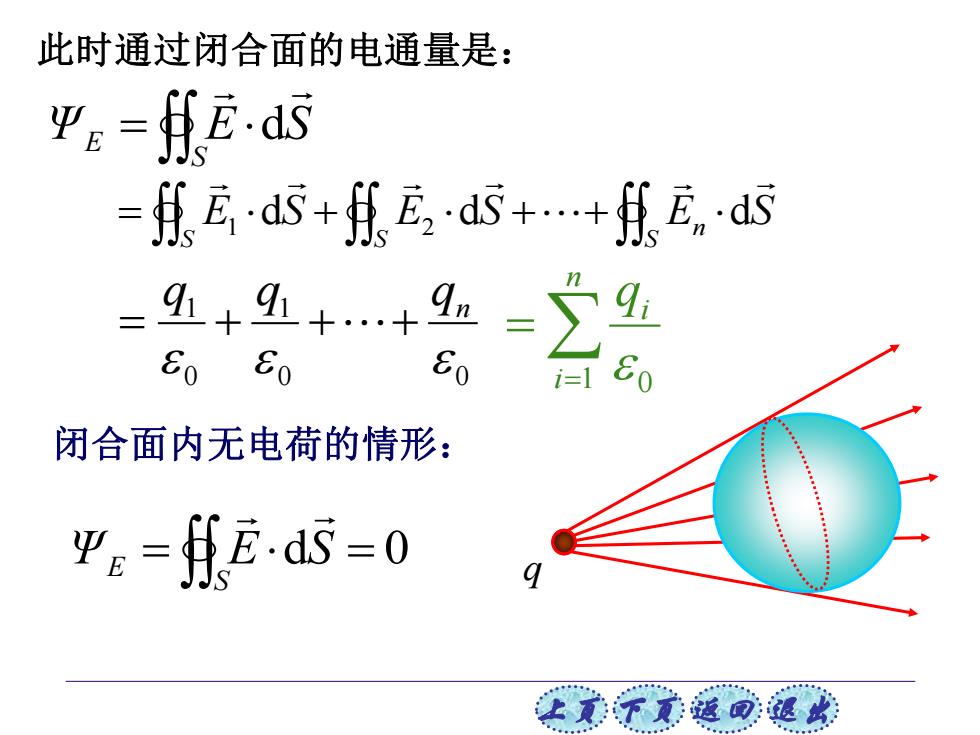
此时通过闭合面的电通量是: 平s=fE.ds =f瓦ds+、瓦,ds++乐瓦,d -4+9++9弘=4 i=1 闭合面内无电荷的情形: 平e=fE.d=0 让美觉返司退
上页 下页 返回 退出 此时通过闭合面的电通量是: 0 0 1 0 1 q q qn = + ++ = = n i qi 1 0 闭合面内无电荷的情形: q = S ΨE E S d E S E S E S S n S S = 1 d + 2 d + + d = d = 0 S ΨE E S

1.当点电荷在球心时 亚。=月E.d =9 2.任一闭合曲面S包围该电荷 %:fe.d=9 0 3.闭合曲面S不包围该电荷 %:=fE.a5=0 4.闭合曲面S包围多个电荷q1~qk,同时面外也有多个 电荷qk+1~qn ∑9 %=jE.ds= 综合以上讨论,可 得如下的结论: 80
上页 下页 返回 退出 1.当点电荷在球心时 Ψ E S S E = d 0 q = 2.任一闭合曲面S包围该电荷 0 q Ψ E S = S E = d 3.闭合曲面S不包围该电荷 = d = 0 Ψ E S S E 4.闭合曲面S包围多个电荷q1 ~qk,同时面外也有多个 电荷qk+1 ~qn 0 = S内 i q d E S = E S 综合以上讨论,可 得如下的结论:

高斯定理: 在静电场中,通过任意闭合曲面的电通量,等于该 曲面内电荷量代数和除以真空介电常数。 Ψs=fE.ds=。∑g 讨论: 1.当闭合曲面内净电荷为正时,wE>0,表示有电场线 从曲面内穿出,正电荷称为静电场的源头; 2.当闭合曲面内净电荷为负时,圳<0,表示有电场线从 曲面外穿进,负电荷称为静电场的尾闾,当曲面内无净 电荷时,沙ε=0。故静电场是有源场。 让美觉返司退
上页 下页 返回 退出 高斯定理: = = S内 i S ΨE E S q 0 1 d 在静电场中,通过任意闭合曲面的电通量,等于该 曲面内电荷量代数和除以真空介电常数。 1.当闭合曲面内净电荷为正时, ψE >0,表示有电场线 从曲面内穿出,正电荷称为静电场的源头; 2.当闭合曲面内净电荷为负时,ψE<0,表示有电场线从 曲面外穿进,负电荷称为静电场的尾闾,当曲面内无净 电荷时, ψE =0。故静电场是有源场。 讨论: