§7-10静电场的能量 在电场中电荷移动电场力对电荷作功,说明电场 蕴藏着能量一一静电能。电容器充放电过程中的现象 则是电场能和其它能量相互转化的结果。 静电场的能量特征 如图,电容器充电过程 是把微小电荷+dg移到另一 个极板,结果,两极板带等 +dg 量异种电荷。 外力作劝 设电容器极板带电荷量为 极板间电势差为-以 让美下元返回:退欢
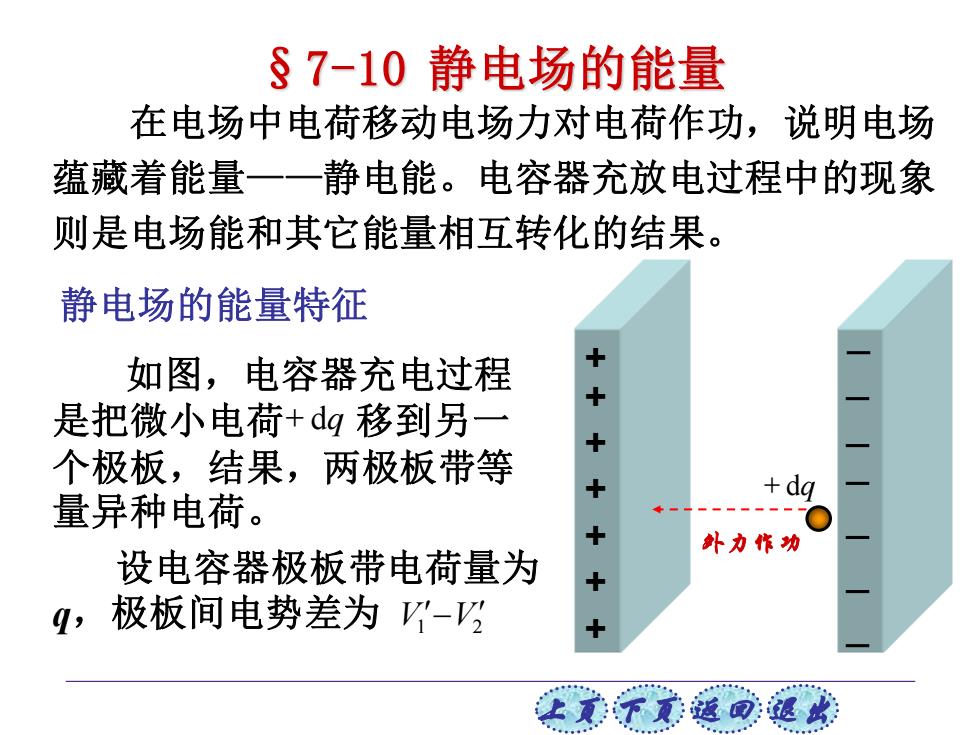
上页 下页 返回 退出 如图,电容器充电过程 是把微小电荷 移到另一 个极板,结果,两极板带等 量异种电荷。 §7-10 静电场的能量 V1 V2 − + dq 在电场中电荷移动电场力对电荷作功,说明电场 蕴藏着能量——静电能。电容器充放电过程中的现象 则是电场能和其它能量相互转化的结果。 静电场的能量特征 + + + + + + + 设电容器极板带电荷量为 q,极板间电势差为 + dq 外力作功

把微小电荷+dg移到另一个极板外力克服电场力作功 d4=(V-V2)dq 电容器电容为C,此时带电量为g,?-=号 所以 C 当电容器由q=0到9=Q 1-时-幽% 这个功应等于电容器的静电能。Q=C心-'2) 则电容器的静电能为
上页 下页 返回 退出 电容器电容为C,此时带电量为q, C q V1 −V2 = 所以 d d q A q C = 当电容器由 q = 0 到 q = Q 这个功应等于电容器的静电能。 ( ) Q =C V1 −V2 则电容器的静电能为 把微小电荷 + dq 移到另一个极板外力克服电场力作功 d d A V V q = − ( 1 2 ) C Q q C q A A Q 2 0 2 1 = d = d =

w=,g-2c-y=-5) 2C2 下面说明静电能也就是电场的能量,且分布在电场 所占的整个空间之中。 设平行板面积为S两极板间距为d`、 极板间电势差为<U2=Ed又C=eSd 电场所占体积 由上式可见,静电能可用表征电场性质的电场强度E 表示,且与电场所古体积成正比。这表明电能储存 在电场中。 让美下觉返司速此
上页 下页 返回 退出 ( ) ( ) 1 2 2 1 2 2 2 1 2 1 2 1 C V V Q V V C Q W = = − = − 下面说明静电能也就是电场的能量,且分布在电场 所占的整个空间之中。 设平行板面积为 S 两极板间距为 d 极板间电势差为 U12 = Ed 又 C = S d W C(V V ) E Sd E V 2 2 2 1 2 2 1 2 1 2 1 = − = = 电场所占体积 由上式可见,静电能可用表征电场性质的电场强度E 表示,且与电场所占体积成正比。这表明电能储存 在电场中

静电场的能量 匀强电场的能量即=)CU%=201=2a07 匀强电场的电场能量密度为w。= =DE 一 般情况下,电场能量密度为 w。= D.E 2 各向同性介质中,电场能量密度为 任一带电体系的电场总能量 w=∫w,d业=j川2D-aW 让贰不觉返回退
上页 下页 返回 退出 静电场的能量 匀强电场的能量 W CU E Sd E V 2 2 2 AB 2 1 2 1 2 1 = = = 匀强电场的电场能量密度为 E DE V W w 2 1 = 2 1 = = 2 e 任一带电体系的电场总能量 W w V D E V V d 2 1 e d = = 一般情况下,电场能量密度为 w D E = 2 1 e 各向同性介质中,电场能量密度为 2 e 2 1 w = E

例题7-31计算均匀带电球体的电场能量,设球半径为 R,带电量为g,球外为真空。 解:均匀带电球体内外的电场强度分布为 E= 1 (r<R) E- ,(≥R) 4π8R 相应的,球内外的电场能量密度为 92r2 32π2GnR6 (r<R) 1 w。= (4π, 32元26r (r≥R) 让美觉返司退此
上页 下页 返回 退出 例题7-31 计算均匀带电球体的电场能量,设球半径为 R,带电量为q,球外为真空。 3 0 ( ) 4π Qr E r R R = 3 0 1 ( ) 4π Qr E r R r = , 解:均匀带电球体内外的电场强度分布为 相应的,球内外的电场能量密度为 6 0 2 2 2 2 3 0 e 0 2 4π 32π 1 R q r R qr w = = (r < R) 2 2 e 0 2 2 4 0 0 1 2 4π 32π q q w r r = = (r ≥R)