966 当观测到一个x值后,则x的条件错误概率: 决策为w2时) P(w,Ix)当P(w2|x)>P(WIx)时 P(elx)= P(w2|x)当P(,x)>P(w2x)时 p(x @)P(@) (决策为w时) p(z l@2)P(@2) 图2.3 t为两类的分界面 p(w2)P2(e) p(w1)P1(e) (判决门限) 巩1 死2 x 图2.3错误率
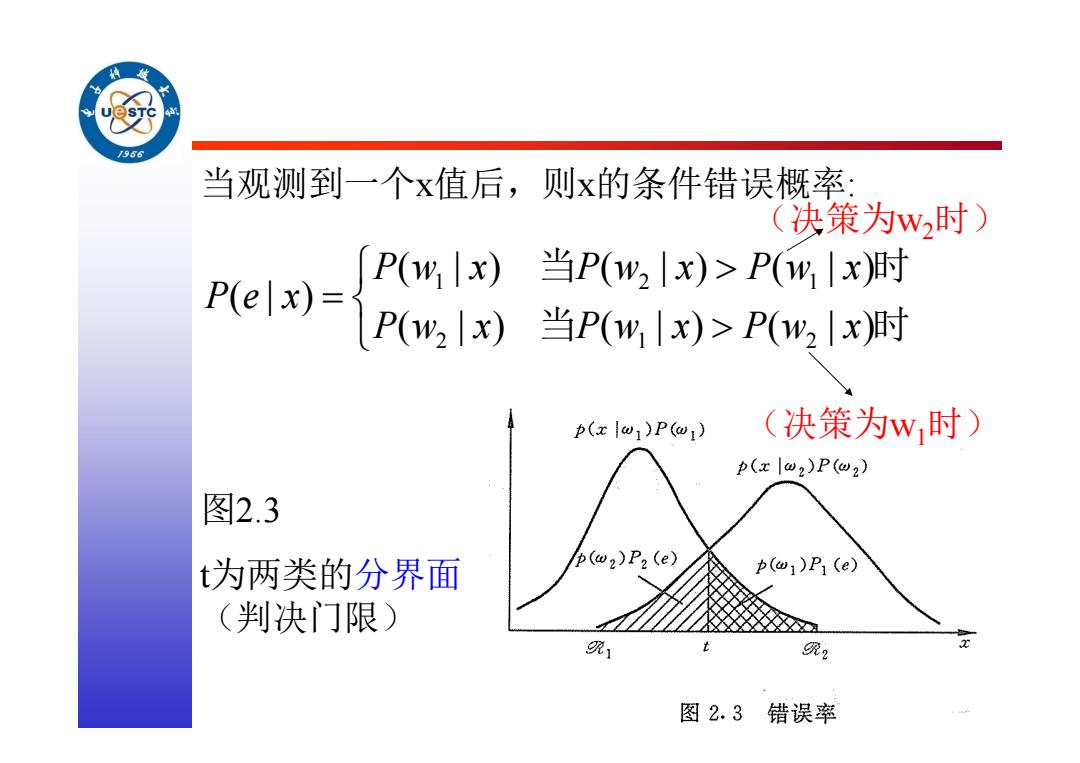
图2.3 t为两类的分界面 (判决门限) 1 21 2 12 ( |) ( |) ( |) (|) ( |) ( |) ( |) Pw x Pw x Pw x Pe x Pw x Pw x Pw x 当 时 当 时 当观测到一个x值后,则x的条件错误概率: (决策为w2时) (决策为w1时)
966 在一维特征空间里,为x轴上一个点,分类器将特 征空间划分成两个区域:R,R2 p(x w1)P(@1) p(x|w2)P(w2) 在区域R,中 p(u2)P2(e) p(ω1)P1(e) 1 2 图2.3错误率 p(xw)P(W)>p(xW2)P(W2 在区域R2中 p(x W2)P(w2)>p(xw)P(W)
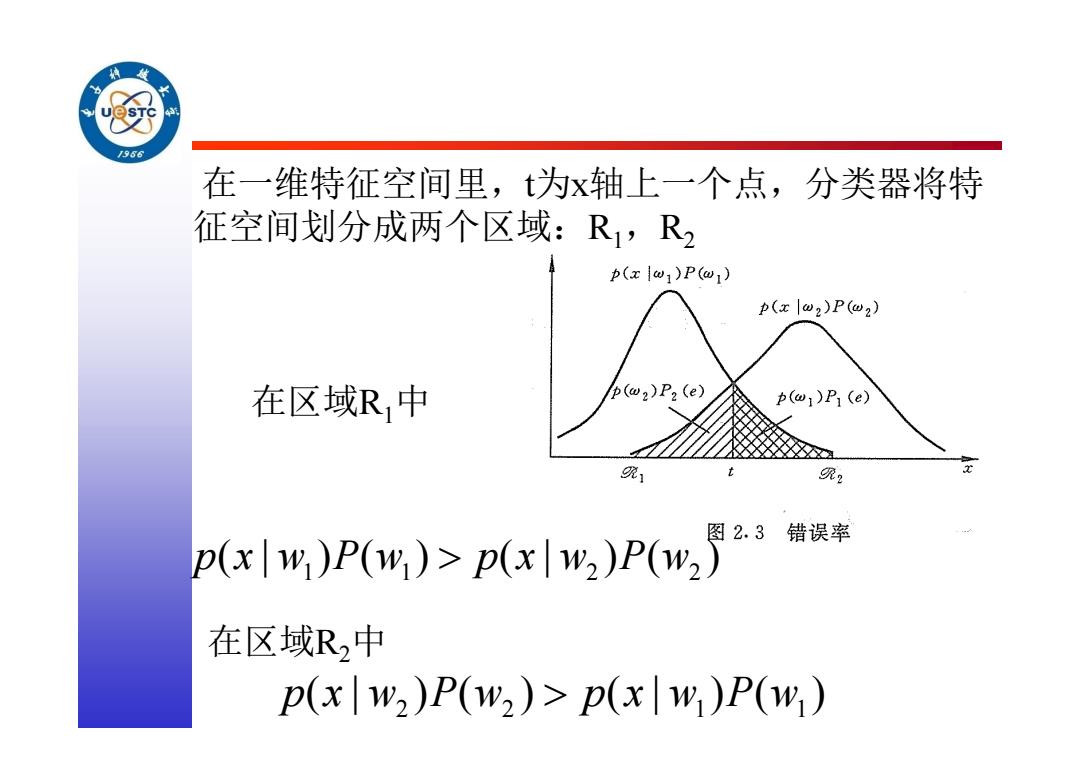
在一维特征空间里, t 为 x轴上一个点,分类器将特 征空间划分成两个区域: R 1,R 2 在区域 R 1 中 11 2 2 p(| )( ) (| )( ) x w Pw px w Pw 2 2 11 p(| )( ) (| )( ) x w Pw px w Pw 在区域 R 2 中
/986 显然,分类错误包含两种情况: >一是x∈w1,而判为w2,图中方格区域 >二是x∈w2,而判为w1,图中斜纹区域 p(x lw)P(@) ∫P(w,x)px)dk p(x o2)P(@2) =」np(xw2)P(w2)d (u2)P2(e) p(w1)P1(e) 观2 x P(p(x)dx 图2.3错误率 p(x)P(w )dx
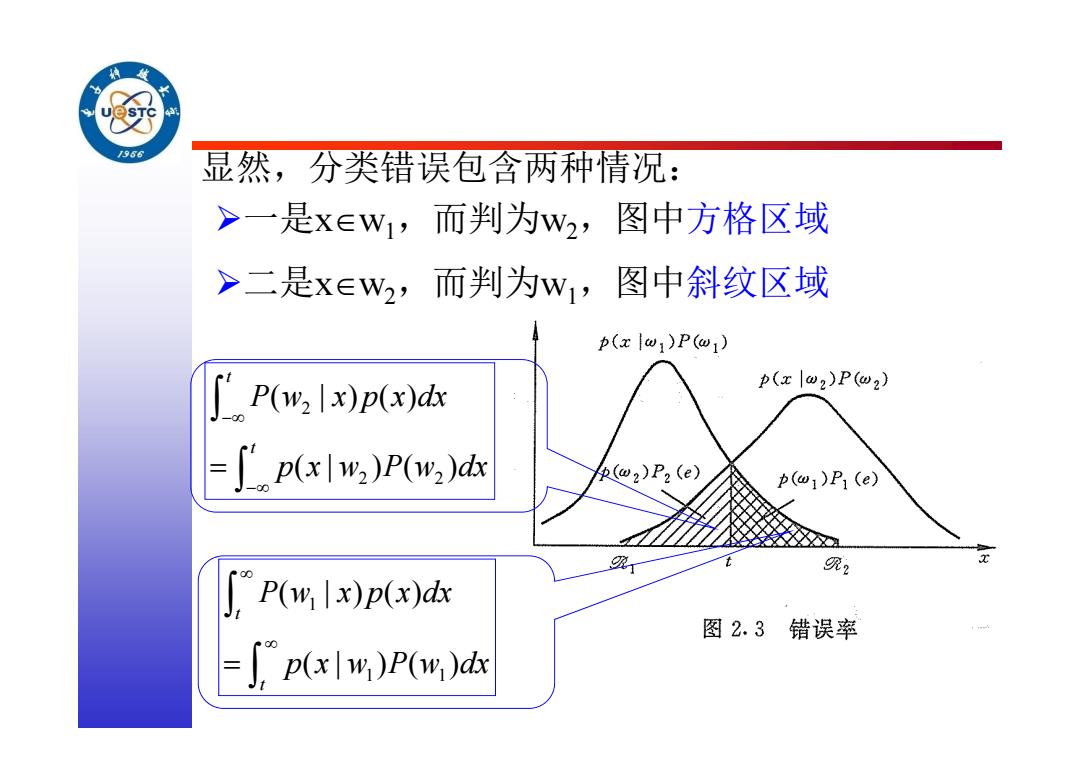
二是xw2,而判为w1,图中斜纹区域 显然,分类错误包含两种情况: 一是xw1,而判为w2,图中方格区域 2 2 2 ( | ) () (| )( ) t t P w x p x dx p x w P w dx 1 1 1 ( | ) () (| )( ) t t P w x p x dx p x w P w dx

/986 条件错误率p(ex)是x函数,对于大量样本x,则总 的错误概率是p(ex)的数学期望。 总错误率为: P(e)=p(elx)p(x)dx =[P(w2Ix)p(xdx+P(p(x)d -p(xIw)P(w)ds+"(xI)P()dx P(w2)p(xlw2)dx+P(w)p(xw)dx =P(w2)p2(e)+P(w)p(e)阴影面积
条件错误率p(e|x)是x函数,对于大量样本x,则总 的错误概率是p(e|x)的数学期望。 总错误率为: 2 1 2 2 11 2 21 1 22 1 1 () ( | ) () ( | ) () ( | ) () ( | )( ) ( | )( ) () ( | ) () ( | ) ( ) () ( ) () t t t t t t P e p e x p x dx P w x p x dx P w x p x dx p x w P w dx p x w P w dx P w p x w dx P w p x w dx Pw p e Pw p e 阴影面积

966 t不同,阴影面积不同,P(e)也不同。 (若改为t,阴影面积增大) ∴.按式2-2或2-3决策,即选择在图2-3图示位置, 使得对每个x,p(ex)为最小,则p(e)也最小。 ·.该决策准则测使平均错误率最小,称为最小错 误率贝叶斯决策规则
t不同,阴影面积不同,P(e)也不同。 按式2-2或2-3决策,即t选择在图2-3图示位置, 使得对每个x,p(e|x)为最小,则p(e)也最小。 该决策准则使平均错误率最小,称为最小错 误率贝叶斯决策规则。 (若改为t1,阴影面积增大)