
核心心重难探究 解:.在△ABC中,AB的垂直平分线分别交AB,AC于点E,D, ‘AD=BD ."△BCD周长为45,AC=25, ..BD+CD+BC-AD+CD+BC=AC+BC-45. .∴.BC=45-25=20. 【方法归纳】 解答此类问题主要运用线段垂直平分线的性质,难度不大, 注意转化思想的应用. 导航页
导航页 核心重难探究 解:∵在△ABC中,AB的垂直平分线分别交AB,AC于点E,D, ∴AD=BD. ∵△BCD周长为45,AC=25, ∴BD+CD+BC=AD+CD+BC=AC+BC=45, ∴BC=45-25=20. 【方法归纳】 解答此类问题主要运用线段垂直平分线的性质,难度不大, 注意转化思想的应用

核心重难探究 知识点二线段垂直平分线的作图 【例2】如图,一辆汽车在笔直的公路 M AB上由A向B行驶,M,N分别是位于公路 AB两侧的村庄,当汽车行驶到哪个位置 A 时,与村庄M,N的距离相等? 思路点拨:因为线段垂直平分线上的点到这条线段两个端点 的距离相等,所以所求位置在线段MN的垂直平分线与公路 AB的交点处 导航页
导航页 核心重难探究 知识点二 线段垂直平分线的作图 【例2】如图,一辆汽车在笔直的公路 AB上由A向B行驶,M,N分别是位于公路 AB两侧的村庄,当汽车行驶到哪个位置 时,与村庄M,N的距离相等? 思路点拨:因为线段垂直平分线上的点到这条线段两个端点 的距离相等,所以所求位置在线段MN的垂直平分线与公路 AB的交点处
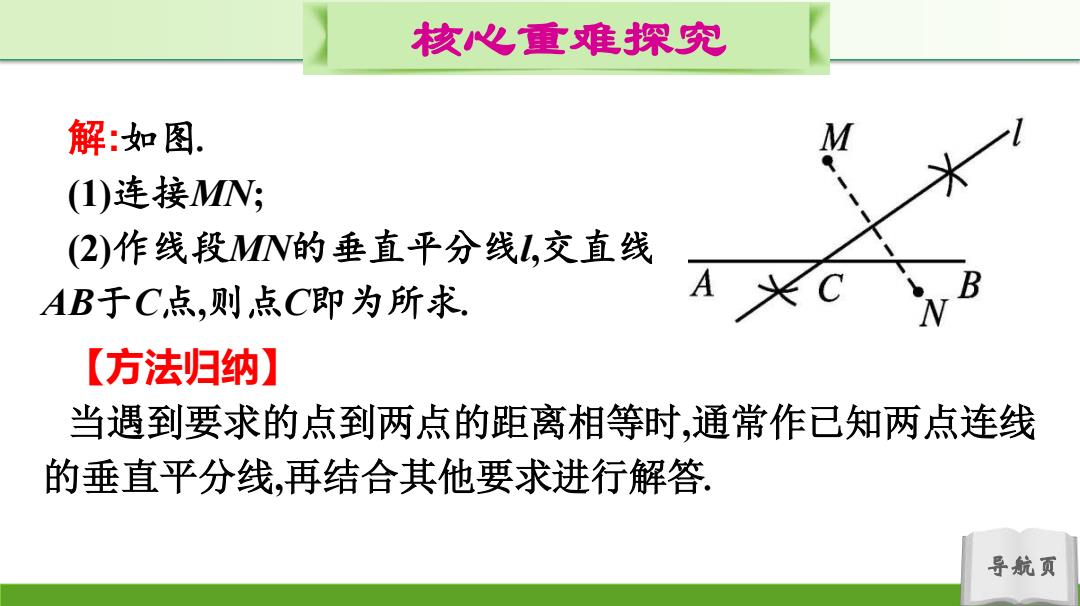
核心重难探究 解:如图。 M (1)连接MN; (2)作线段MN的垂直平分线L,交直线 AB于C点,则,点C即为所求, A 【方法归纳】 当遇到要求的点到两点的距离相等时,通常作已知两点连线 的垂直平分线,再结合其他要求进行解答. 导航页
导航页 核心重难探究 解:如图. (1)连接MN; (2)作线段MN的垂直平分线l,交直线 AB于C点,则点C即为所求. 【方法归纳】 当遇到要求的点到两点的距离相等时,通常作已知两点连线 的垂直平分线,再结合其他要求进行解答