
家庭侯亚 3.探索三角形全等的条件 第2课时 角边角、角角边
3.探索三角形全等的条件 第2课时 角边角、角角边

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.两角及其 夹边 分别相等的两个三角形全等,简写成 “角边角”或“ASA”. 2.两角分别相等且其中一组等角的对 边相等的两 个三角形全等,简写成“角角边”或“AAS”. 温馨提示 由于三角形的内角和为180°,当两个角相等时,第三个角也 相等,所以能利用“AAS”判定全等,也一定能利用“ASA”判定 全等. 导航页
导航页 基础自主梳理 1.两角及其 分别相等的两个三角形全等,简写成 “ ”或“ ” . 2.两角分别相等且其中一组等角的 边相等的两 个三角形全等,简写成“ ”或“ ” . 温馨提示 由于三角形的内角和为180° ,当两个角相等时,第三个角也 相等,所以能利用“AAS”判定全等,也一定能利用“ASA”判定 全等. 夹边 角边角 ASA 对 角角边 AAS
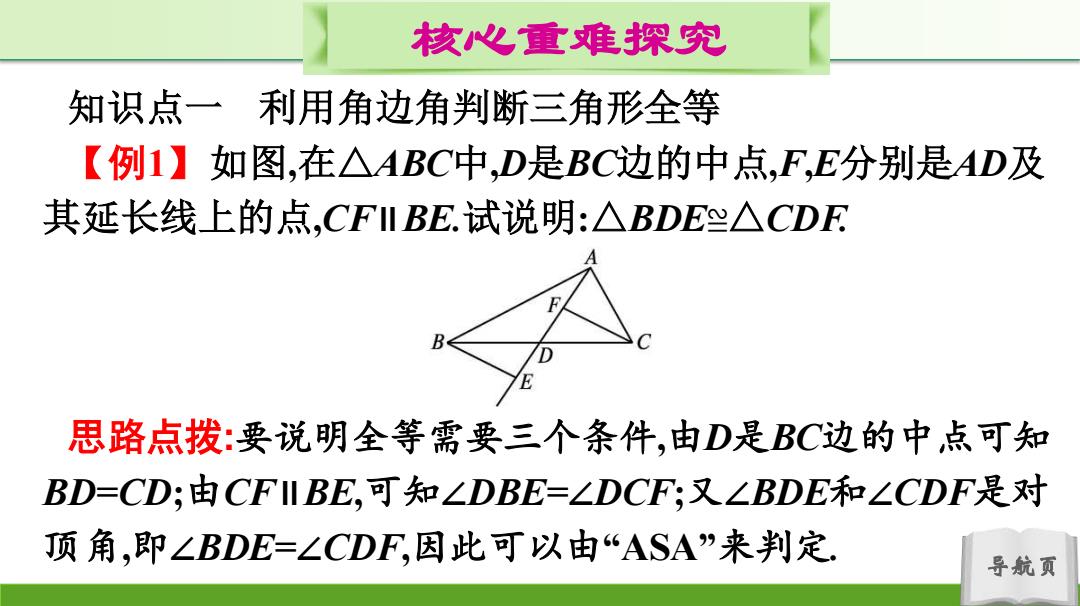
核心重难探究 知识点一利用角边角判断三角形全等 【例1】如图,在△ABC中,D是BC边的中点,F,E分别是AD及 其延长线上的点,CFI BE.试说明:△BDE兴△CDF 思路点拨:要说明全等需要三个条件,由D是BC边的中点可知 BD=CD;由CFII BE,可知∠DBE=∠DCF,又∠BDE和∠CDF是对 顶角,即∠BDE=∠CDF,因此可以由“ASA”来判定, 导航页
导航页 核心重难探究 知识点一 利用角边角判断三角形全等 【例1】如图,在△ABC中,D是BC边的中点,F,E分别是AD及 其延长线上的点,CF∥BE.试说明:△BDE≌△CDF. 思路点拨:要说明全等需要三个条件,由D是BC边的中点可知 BD=CD;由CF∥BE,可知∠DBE=∠DCF;又∠BDE和∠CDF是对 顶角,即∠BDE=∠CDF,因此可以由“ASA”来判定

核心重难探究 解:D是BC的中点, ‘BD=CD .CFIl BE, .∴.∠DBE=∠DCF ∠DBE=∠DCF, 在△BDE和△CDF中,BD=CD, ∠BDE=∠CDF, .'.△BDE≈△CDF(ASA). 【方法归纳】 本题挖掘隐含条件“对顶角相等”是解答的关键 导航页
导航页 核心重难探究 解:∵D是BC的中点, ∴BD=CD. ∵CF∥BE, ∴∠DBE=∠DCF. 在△BDE 和△CDF 中, ∠𝑫𝑩𝑬 = ∠𝑫𝑪𝑭, 𝑩𝑫 = 𝑪𝑫, ∠𝑩𝑫𝑬 = ∠𝑪𝑫𝑭, ∴△BDE≌△CDF(ASA). 【方法归纳】 本题挖掘隐含条件“对顶角相等”是解答的关键