
家庭馆亚 第四章 三角形 5.利用三角形全等测距离
第四章 三角形 5.利用三角形全等测距离

基础自主梳理 导 核心心重难探究 航 新知训川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自主梳理 1.当两点可以直接到达时,我们可以直接测量出两点之间的 距离;当两点不可以直接到达时,我们可以通过构造全等三 角形的方法来测量两点之间的距离. 温馨提示 利用三角形全等解决实际问题的步骤:()明确实际问题应 用哪些知识来解决;2)根据实际问题抽象出几何图形;3)结合 图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰 当的解决途径,并表述清楚 导航页
导航页 基础自主梳理 1.当两点可以直接到达时,我们可以直接测量出两点之间的 距离;当两点不可以直接到达时,我们可以通过构造 三 角形的方法来测量两点之间的距离. 温馨提示 利用三角形全等解决实际问题的步骤:(1)明确实际问题应 用哪些知识来解决;(2)根据实际问题抽象出几何图形;(3)结合 图形和题意分析已知条件;(4)找到已知与未知的联系,寻求恰 当的解决途径,并表述清楚. 全等
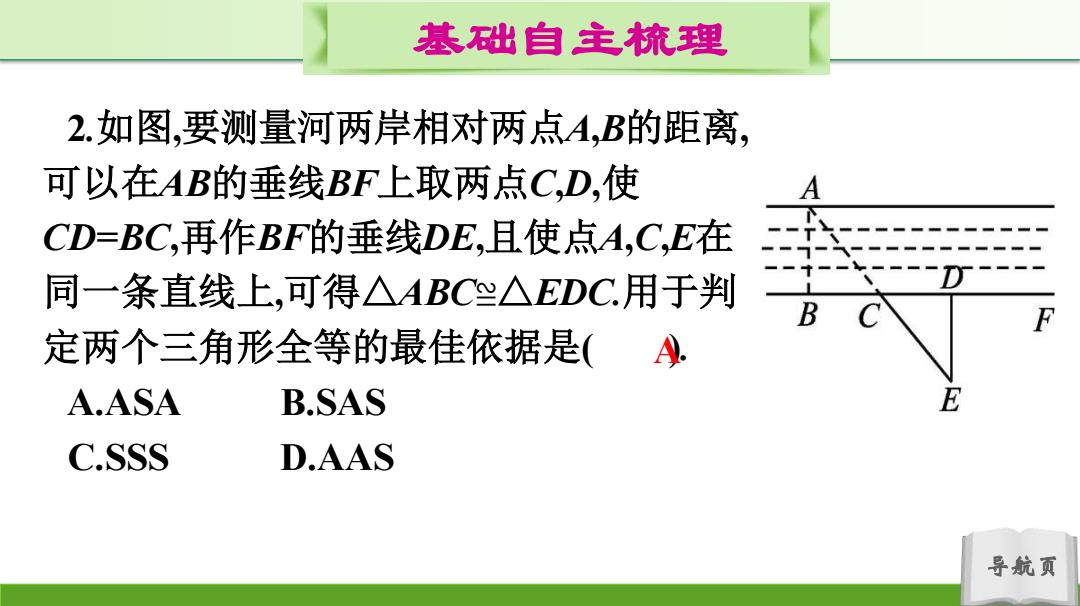
基础自主梳理 2.如图,要测量河两岸相对两点A,B的距离, 可以在AB的垂线BF上取两点C,D,使 A CD=BC,再作BF的垂线DE,且使点A,C,E在 同一条直线上,可得△ABC兰△EDC.用于判 -D B C F 定两个三角形全等的最佳依据是(). A.ASA B.SAS E C.SSS D.AAS 导航页
导航页 基础自主梳理 2.如图,要测量河两岸相对两点A,B的距离, 可以在AB的垂线BF上取两点C,D,使 CD=BC,再作BF的垂线DE,且使点A,C,E在 同一条直线上,可得△ABC≌△EDC.用于判 定两个三角形全等的最佳依据是( ). A.ASA B.SAS C.SSS D.AAS A
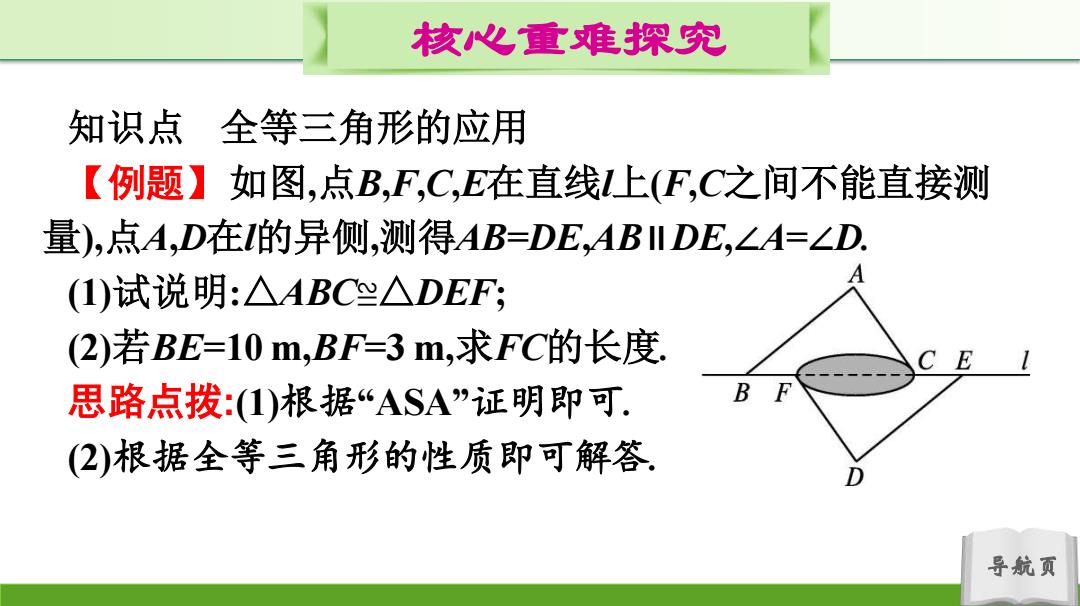
核心重难探究 知识点 全等三角形的应用 【例题】如图,点B,F,C,E在直线1上(F,C之间不能直接测 量),点A,D在I的异侧,测得AB=DE,ABIIDE,∠A=∠D. (1)试说明:△ABC坐△DEF; 2)若BE=10m,BF=3m,求FC的长度. C E 思路点拨:(1)根据“ASA”证明即可. B F (2)根据全等三角形的性质即可解答」 导航页
导航页 核心重难探究 知识点 全等三角形的应用 【例题】如图,点B,F,C,E在直线l上(F,C之间不能直接测 量),点A,D在l的异侧,测得AB=DE,AB∥DE,∠A=∠D. (1)试说明:△ABC≌△DEF; (2)若BE=10 m,BF=3 m,求FC的长度. 思路点拨:(1)根据“ASA”证明即可. (2)根据全等三角形的性质即可解答