
若v为整数,V=m=0,1,2,. Jn(x)l IN() Jn(x)与)n(x)线性相关 -宫m广-玄4 2k+ m=0时,显然满足 讨论m=1,2,3,.情况,当k=0,1,2,.,(m-1)时, k-(m-1)s0,r(-nm)=o(n=0,12,) -2mn-2周
6 若为整数, = m = 0, 1, 2, . ( ) ( ) ~ , m m J x R N x J x J x m m ( ) ( ) 与 − 线性相关 ( ) ( ) ( ) 2 0 ! 1 2 k k m m k x J x k k m + = − = + + ( ) ( ) 2 0 ! ! 2 k k m k x k k m + = − = + ( ) ( ) ( ) 2 0 ! 1 2 k k m m k x J x k k m − − = − = − + m = 0 时,显然满足. 讨论m = 1, 2, 3, .情况,当k = 0, 1, 2, . , (m -1 )时, k m n n − − − = = ( 1 0, 0,1,2, ) ( ) ( ) ( ) ( ) ( ) 2 0 ! 1 2 k k m m k x J x k k m − − = − = − + ( ) ( ) 2 ! 1 2 k k m k m x k k m − = − = − +

2k +m -含e周6rw 2k +m 因此,m阶贝塞耳方程的解为: 若R=有界,→R~Jm(x) N()=.()osr-’,因) v阶诺尔曼函数 sin va N (x)=lim J(x)cosvz-Jv(x) nm阶诺尔曼函数 sin Va 当x→0时,Nm(c)→o.若要求x=0有界,则应排除Nm(x)
7 ' 令k m k − = , ( ) ( ) ( ) ( ) ' ' ' 2 ' ' 0 ! 1 2 k m k m m k x J x k m k + + − = − = + + ( ) ( ) ( ) ' ' ' 2 ' ' 0 ! ! 2 k k m m k x k m k + = − = − + ( ) ( ) m m = − J x 因此,m 阶贝塞耳方程的解为: ( ) ( ) ~ , m m J x R N x ( ) 0 ~ . 若R R J x x= = 有界, m ( ) ( ) cos ( ) sin J x J x N x − − = —— 阶诺尔曼函数 ( ) ( ) cos ( ) lim sin m m J x J x N x − → − = —— m阶诺尔曼函数 当x → 0时,Nm (x) → . 若要求x = 0有界,则应排除Nm (x)

H()=J()+iN () 第一种汉克函数 H2)()-iN (x). 一第二种汉克函数 第一类柱函数一 贝塞耳函数(包括虚贝塞耳函数) 第二类柱函数 诺尔曼函数(包括虚诺尔曼函数) 第三类柱函数一第一种和第二种汉克函数. 讨论: ① 柱内问题(0≤p≤P) 由于imNm(x)=o,此时应排除m阶诺尔曼函数 x-→0 R-J(Vp) ②柱外或空心圆柱问题 (p2P或P1≤p≤P) 8
8 ( ) ( ) ( ) 1 . H J x iN x m m m = + —— 第一种汉克函数 ( ) ( ) ( ) 2 . H J x iN x m m m = − —— 第二种汉克函数 第一类柱函数——贝塞耳函数(包括虚贝塞耳函数), 第二类柱函数——诺尔曼函数(包括虚诺尔曼函数), 第三类柱函数——第一种和第二种汉克函数. 讨论: ① 柱内问题(0 0) ( ) 0 lim , m x N x → 由于 = 此时应排除m阶诺尔曼函数. R J ~ m ( ) ② 柱外或空心圆柱问题 ( 0 或 1 2 ) ( ) ( ) ~ , m m J R N

③解在x=0点正常 由于imJ,(x)=oo,J 此时应排除-ν阶诺尔曼函数 x→0 S12.3贝塞耳函数的递推公式、母函数、积分表达式 (一)递推公式 (x)+( 2=-Ji(x月 或 .(]=x() J(x)+ 明:内-名rv周 x
9 ③ 解在x = 0点正常 ( ) 0 lim , x J x − → 由于 = 此时应排除- 阶诺尔曼函数. §12.3 贝塞耳函数的递推公式、母函数、积分表达式 (一)递推公式 ( ) ( ) ( ) ( ) 1 1 , . d J x J x dx x x d x J x x J x dx + − = − = 证明: ( ) ( ) ( ) 2 0 ! 1 2 k k k x J x k k + = − = + + ( ) ( ) ( ) 2 2 0 1 ! 1 2 k k k k J x x x k k + = − = + + ( ) ( ) ( ) ( ) ( ) ( ) ' 1 ' 1 ; . J x J x J x x J x J x J x x + − + = − + = 或
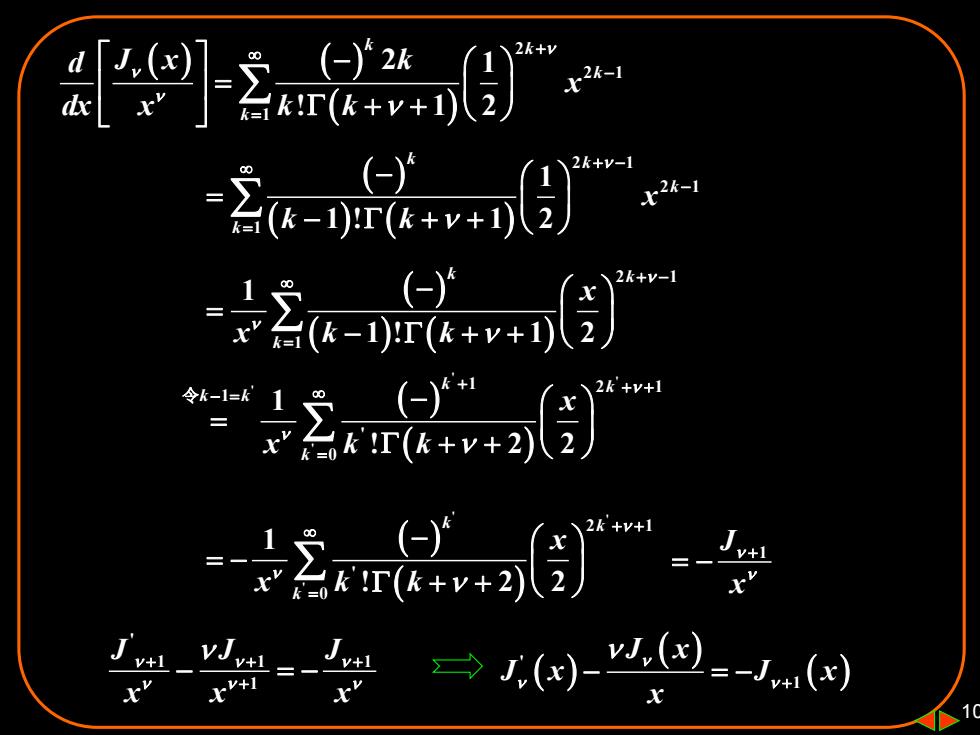
斗-8 k +y+] K +V+ ()- 2=-Ji(x)
10 ( ) ( ) ( ) 2 2 1 1 2 1 ! 1 2 k k k k d J x k x dx k k x + − = − = + + ( ) ( ) ( ) 2 1 2 1 1 1 1 ! 1 2 k k k k x k k + − − = − = − + + ( ) ( ) ( ) 2 1 1 1 1 ! 1 2 k k k x x k k + − = − = − + + ( ) ( ) ' ' ' ' 1 2 1 1 ' 0 1 ! 2 2 k k k k k x x k k + + + − = = − = + + 令 ( ) ( ) ' ' ' 2 1 ' 0 1 ! 2 2 k k k x x k k + + = − = − + + 1 J x + = − ' 1 1 1 1 J J J x x x + + + + − = − ( ) ( ) ( ) ' 1 J x J x J x x − = − +