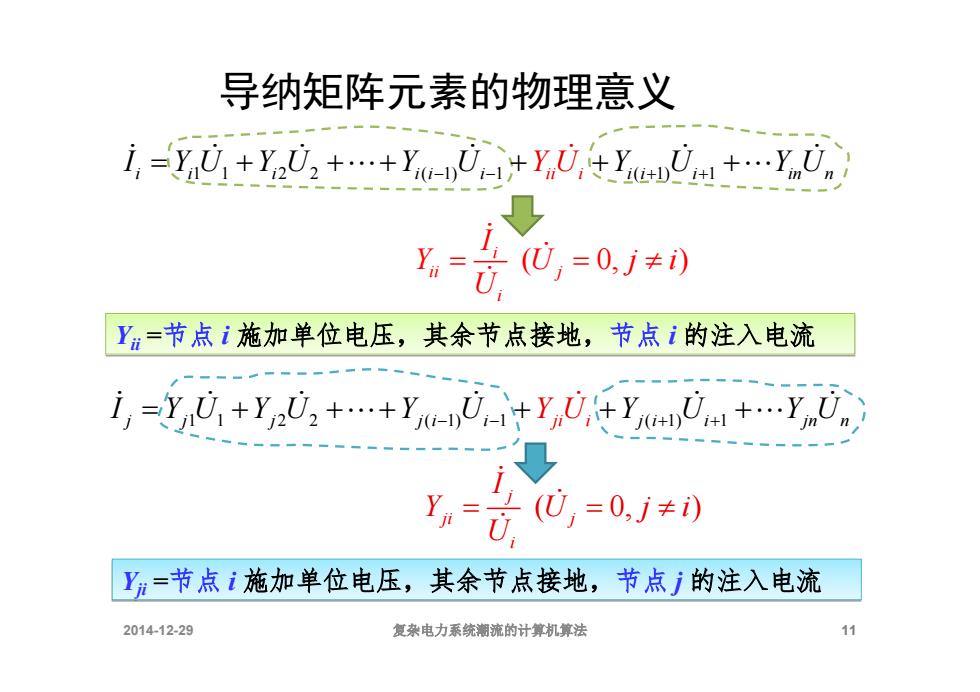
导纳矩阵元素的物理意义 i,=-+y03++y-0+y+y+.Y (,=0,1≠) Y=节点i施加单位电压,其余节点接地,节点i的注入电流 i,=yU1+YU+.+Y-Uity,Uty+U41+.YnUn Y- (0,=0,j≠i) Y=节点i施加单位电压,其余节点接地,节点j的注入电流 2014-12-29 复杂电力系统潮流的计算机算法 11
2014-12-29 复杂电力系统潮流的计算机算法 11 导纳矩阵元素的物理意义 i i i i i i i i i in 1 1 2 2 ( 1) 1 ( 1) 1 ii i n I Y U Y U Y U Y U Y U Y U ( 0, ) i ii j i I Y U j i U Yiiii =节点 i 施加单位电压,其余节点接地, 施加单位电压,其余节点接地,节点 i 的注入电流 j j j j i i j i i jn 1 1 2 2 ( 1) 1 ( 1) 1 ji i n I Y U Y U Y U Y U Y U Y U ( 0, ) j ji j i I Y U j i U Yjiji =节点 i 施加单位电压,其余节点接地, 施加单位电压,其余节点接地,节点 j 的注入电流
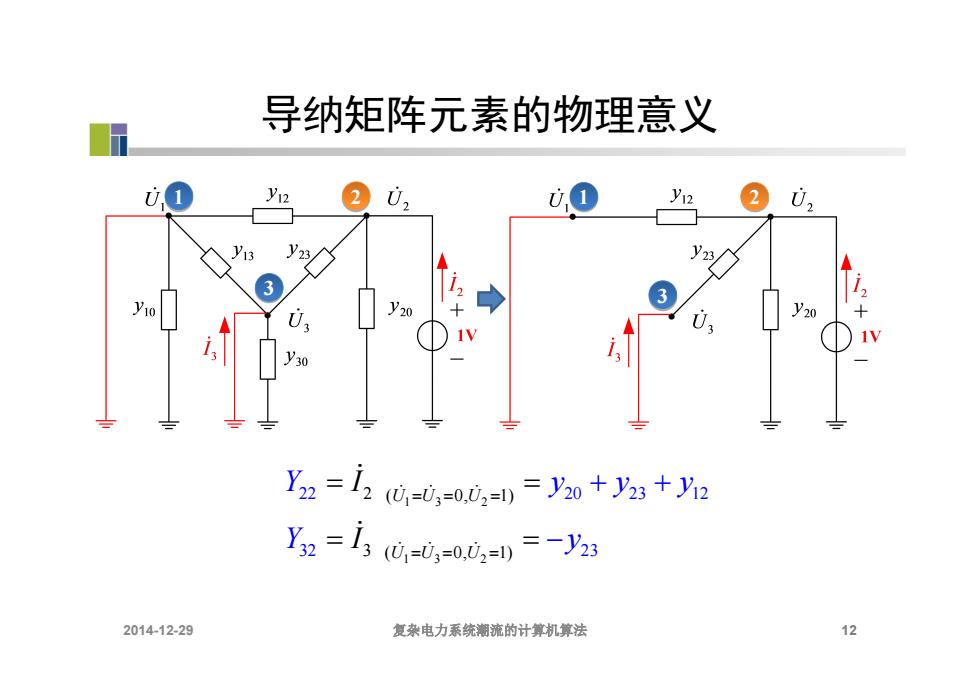
导纳矩阵元素的物理意义 0, Y2=i2G=i,=00==yo+y2:+yn Y2=13=0,=00,=)=-y%3 2014-12-29 复杂电力系统潮流的计算机算法 12
导纳矩阵元素的物理意义 12 3 1 2 3 1 2 1 3 2 1 3 2 2 ( 0, 1) 3 ( 0, 1 22 20 23 12 32 2 ) 3 U U U U U U Y y y y Y y I I 2014-12-29 复杂电力系统潮流的计算机算法

电力网络节点导纳矩阵Y的特点个 n阶方阵,n为网络的独立节点数。 ·复数矩阵。 ·一般为对称方阵(YY)。 ·稀疏矩阵:当节点和节点之间不直接相连时,互导 纳为0。 ·对角元所含的元素个数≥该元素所在行(列)的其它 元素的个数,即互导纳元素都用于形成自导纳;当有 接地支路时,“>”成立。 2014-12-29 复杂电力系统潮流的计算机算法 13
电力网络节点导纳矩阵YB的特点 • n阶方阵, n为网络的独立节点数。 • 复数矩阵。 • 一般为对称方阵 (Yij= Yji)。 • 稀疏矩阵:当节点i和节点j之间不直接相连时,互导 纳为0。 • 对角元所含的元素个数≥该元素所在行(列)的其它 元素的个数,即互导纳元素都用于形成自导纳;当有 接地支路时,“>”成立。 2014-12-29 复杂电力系统潮流的计算机算法 13

节点导纳矩阵的形成和修改 。 Y的形成:给定网络,如何建立节点导纳矩阵 ·方法:根据自导纳和互导纳的基本定义直接生成 自导纳Ya 与节点直接相连的各支路导纳之和 互导纳Y 直接连接于、节点之间各支路导纳之和 的相反数 建议变压器支路采用以导纳表示的Ⅱ型等值电路。 2014-12-29 复杂电力系统潮流的计算机算法 14
节点导纳矩阵的形成和修改 • YB的形成:给定网络,如何建立节点导纳矩阵 • 方法:根据自导纳和互导纳的基本定义直接生成 14 自导纳Yii 与节点i直接相连的各支路导纳之和 互导纳Yij 直接连接于i、j节点之间各支路导纳之和 的相反数 建议变压器支路采用以 建议变压器支路采用以导纳表示的∏型等值电路。 2014-12-29 复杂电力系统潮流的计算机算法

节点导纳矩阵的形成和修改 Y的修改:当网络结构或参数发生变化,如何修改原 YB以形成新的YB (1)从原网络节点i引出一条接地支路 (2)从原网络节点i引出一条支路,并增加节点i (3)在原网络节点i、之间增加一条支路 (4)在原网络节点i、之间切除一条支路 (5)」 原网络节点i、之间的导纳由变为功 (6)原网络i、之间变压器的变比由k变为k 2014-12-29 复杂电力系统潮流的计算机算法 15
节点导纳矩阵的形成和修改 • YB的修改:当网络结构或参数发生变化,如何修改原 YB以形成新的Y′ B 15 (1)从原网络节点 i 引出一条接地支路 (2)从原网络节点 i 引出一条支路,并增加节点j (3)在原网络节点i、j之间增加一条支路 (4)在原网络节点i、j之间切除一条支路 (5)原网络节点i、j之间的导纳由yij变为y'ij (6)原网络i、j之间变压器的变比由k变为k' 2014-12-29 复杂电力系统潮流的计算机算法