《电力系统分析》课程教学课件（讲稿）04 复杂电力系统潮流的计算机算法

4.1电力网络方程 ·节点电压方程 ·节点导纳矩阵的形成和修改 2014-12-29 复杂电力系统潮流的计算机算法 6

4.1 电力网络方程 • 节点电压方程 • 节点导纳矩阵的形成和修改 2014-12-29 复杂电力系统潮流的计算机算法 6

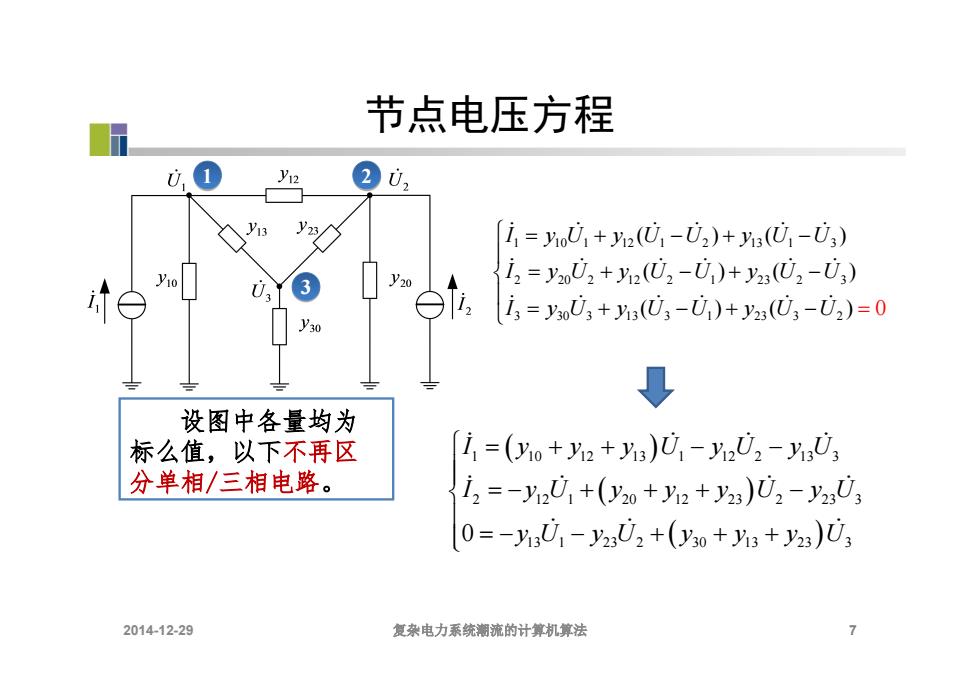
节点电压方程 y12 202 y23/ i=01+2(01-02)+(U1-U3) i2=y202+2(U2-01)+y23(心2-0) i3=y03+h(U3-U1)+y23(U3-U2)=0 ↓ 设图中各量均为 标么值，以下不再区 i=(yo+2+3)U1-y02-0; 分单相/三相电路。 2=-yU1+(y0+y2+y23)U2-2,U 0=-yU1-y23U2+(y3o+3+y23)U 2014-12-29 复杂电力系统潮流的计算机算法

节点电压方程 7 3 1 2 1 10 1 12 1 2 13 1 3 2 20 2 12 2 1 23 2 3 3 30 3 13 3 1 23 3 2 ( 0 ) ( ) ( ) ( ) ( ) ( ) I y U y U U y U U I y U y U U y U U I y U y U U y U U                                              1 10 12 13 1 12 2 13 3 2 12 1 20 12 23 2 23 3 13 1 23 2 30 13 23 3 0 I y y y U y U y U I y U y y y U y U y U y U y y y U                                  设图中各量均为 标么值，以下不再区 分单相/三相电路。 2014-12-29 复杂电力系统潮流的计算机算法

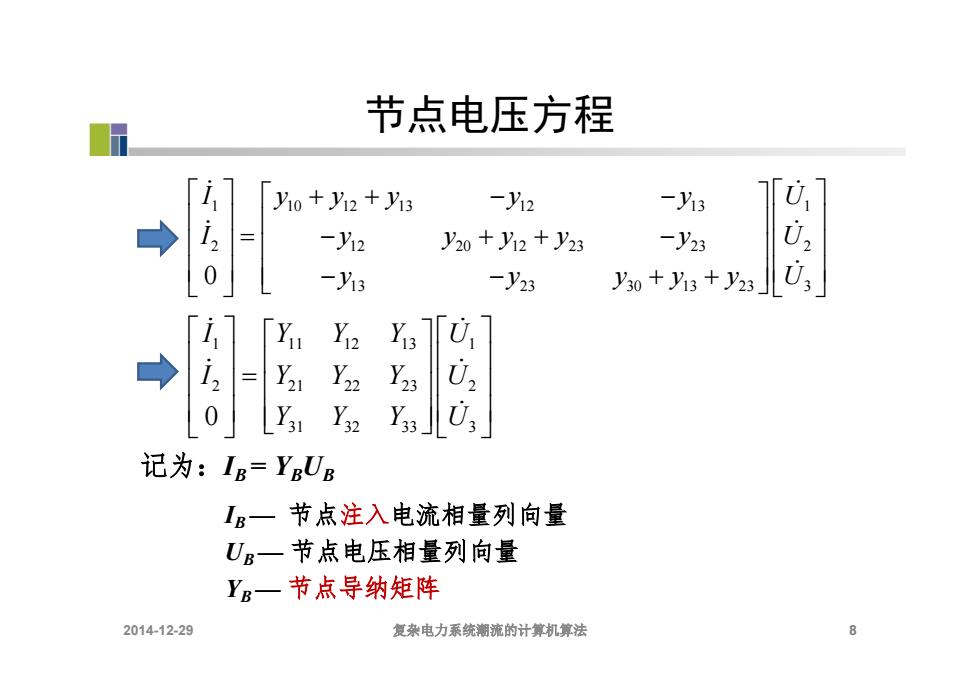
节点电压方程 y10+y12+y13 -y12 -y13 -y12 y20+12+y23 -y23 0 一3 -y23 y30+3+y23 「i [Yu Y2 y → Y Y Y23 0 Y 0 记为：IB=YBUB IB一 节点注入电流相量列向量 UB一节点电压相量列向量 YB一节点导纳矩阵 2014-12-29 复杂电力系统潮流的计算机算法 8

节点电压方程 8 1 10 12 13 12 13 1 2 12 20 12 23 23 2 13 23 30 13 23 3 0 I y y y y y U I y y y y y U y y y y y U                                     1 11 12 13 1 2 21 22 23 2 31 32 33 3 0 I Y Y Y U I Y Y Y U Y Y Y U                         记为：IB = YBUB IB — 节点注入电流相量列向量 UB — 节点电压相量列向量 YB — 节点导纳矩阵 2014-12-29 复杂电力系统潮流的计算机算法

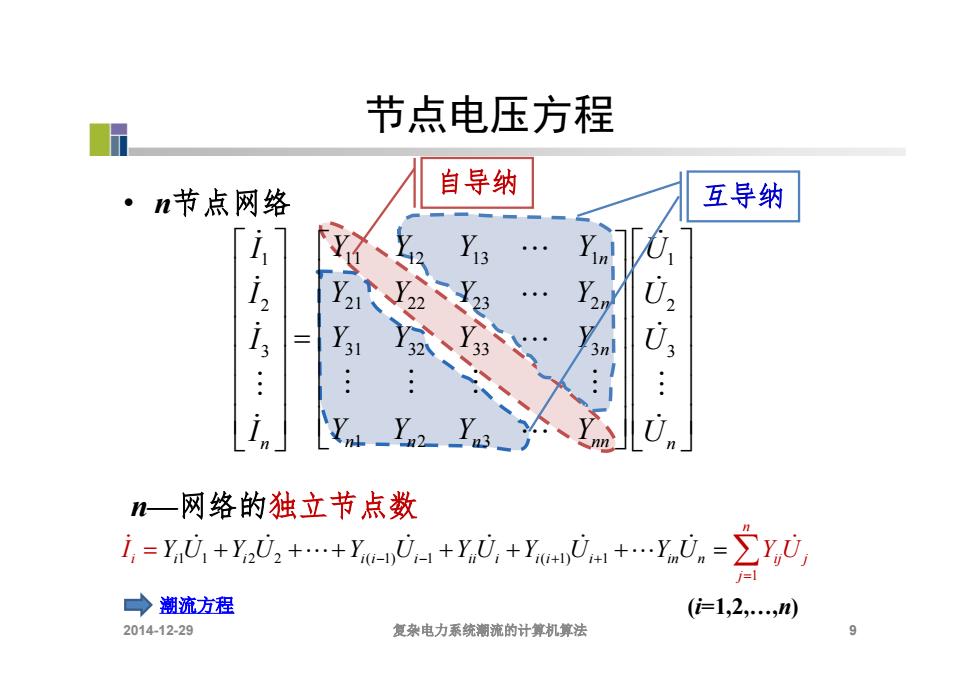
节点电压方程 ·n节点网络 自导纳 互导纳 】13 ·2 n V, n一网络的独立节点数 i=yi,+y,02+.+y0p+y,0,+yunm+.y0.=y, →潮流方程 (=1,2,0) 2014-12-29 复杂电力系统潮流的计算机算法

2014-12-29 节点电压方程 • n节点网络 n—网络的独立节点数 9 1 1 11 12 13 1 2 2 21 22 23 2 3 3 31 32 33 3 1 2 3 n n n n n n n n nn I U Y Y Y Y I U Y Y Y Y I U Y Y Y Y I U Y Y Y Y                                      自导纳 互导纳 1 i i i i i ii i 1 1 2 2 ( 1) 1 ( 1) 1 n i ij j j Y U Y U Y U Y U Y U Y U i i i in n I Y U                         潮流方程 (i=1,2,.,n) 复杂电力系统潮流的计算机算法

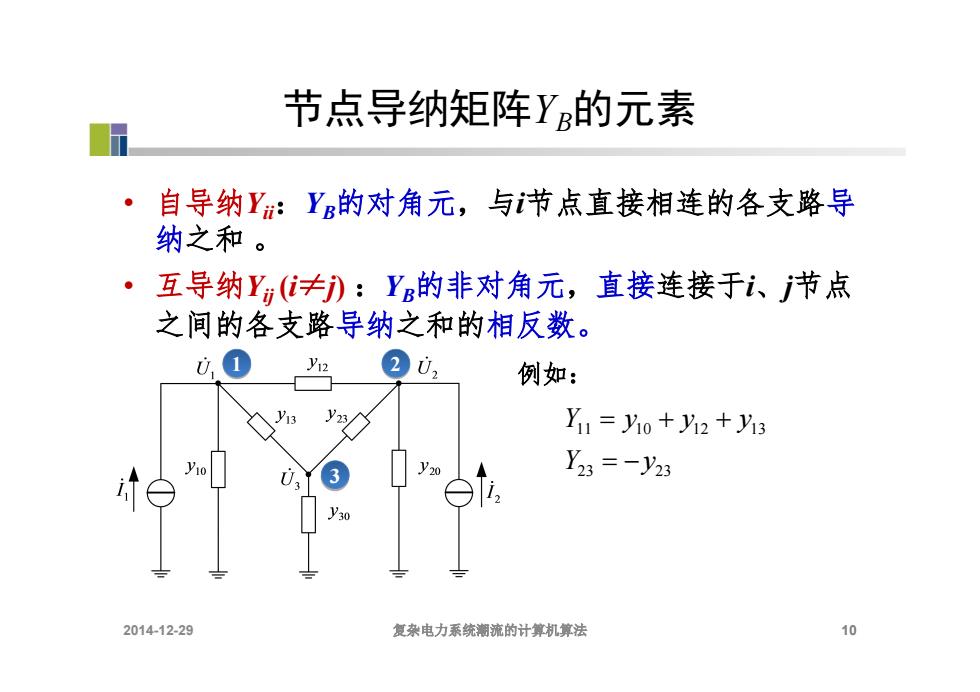
节点导纳矩阵Y的元素 ·自导纳Y:Y的对角元，与节点直接相连的各支路导 纳之和。 ·互导纳Y≠)：Y的非对角元，直接连接于i、节点 之间的各支路导纳之和的相反数。 V12 例如： Y=y0+y12+y13 Y23=-y23 2014-12-29 复杂电力系统潮流的计算机算法 10

节点导纳矩阵YB的元素 • 自导纳Yii：YB的对角元，与i节点直接相连的各支路导 纳之和 。 • 互导纳Yij (i≠j) ：YB的非对角元，直接连接于i、j节点 之间的各支路导纳之和的相反数。 10 3 1 2 11 10 12 13 23 23 Y y y y Y y      例如： 2014-12-29 复杂电力系统潮流的计算机算法