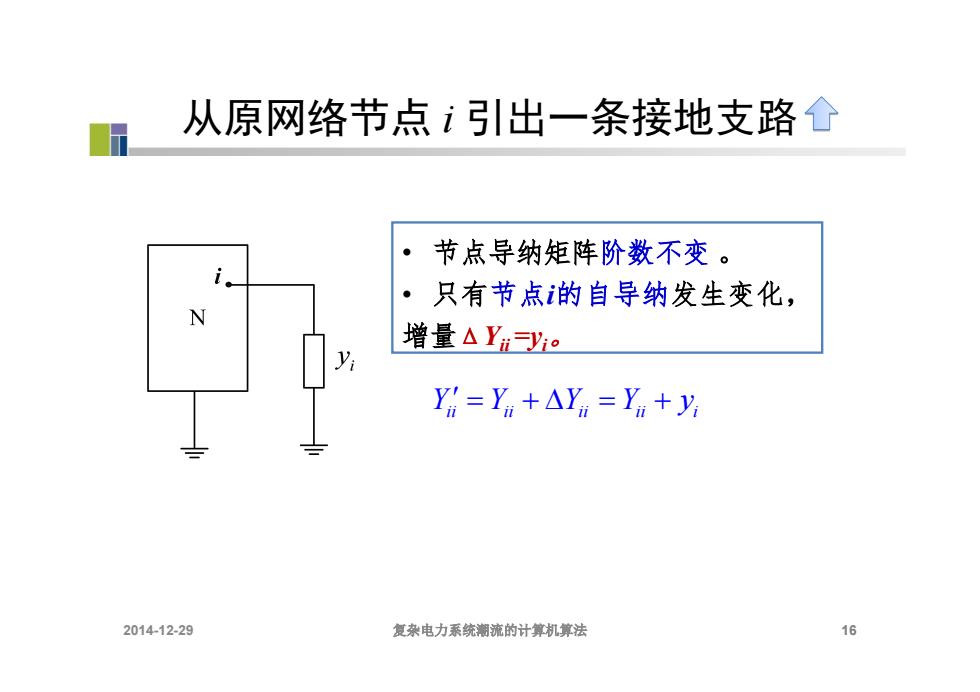
从原网络节点i引出一条接地支路个 。 节点导纳矩阵阶数不变。 ·只有节点的自导纳发生变化, 增量△Yn=yo Y=Yn+△Y=Ym+y 2014-12-29 复杂电力系统潮流的计算机算法 16
从原网络节点 i 引出一条接地支路 16 • 节点导纳矩阵阶数不变 。 • 只有节点i的自导纳发生变化, 增量ΔYii =yi。 Y Y Y Y y ii ii ii ii i 2014-12-29 复杂电力系统潮流的计算机算法
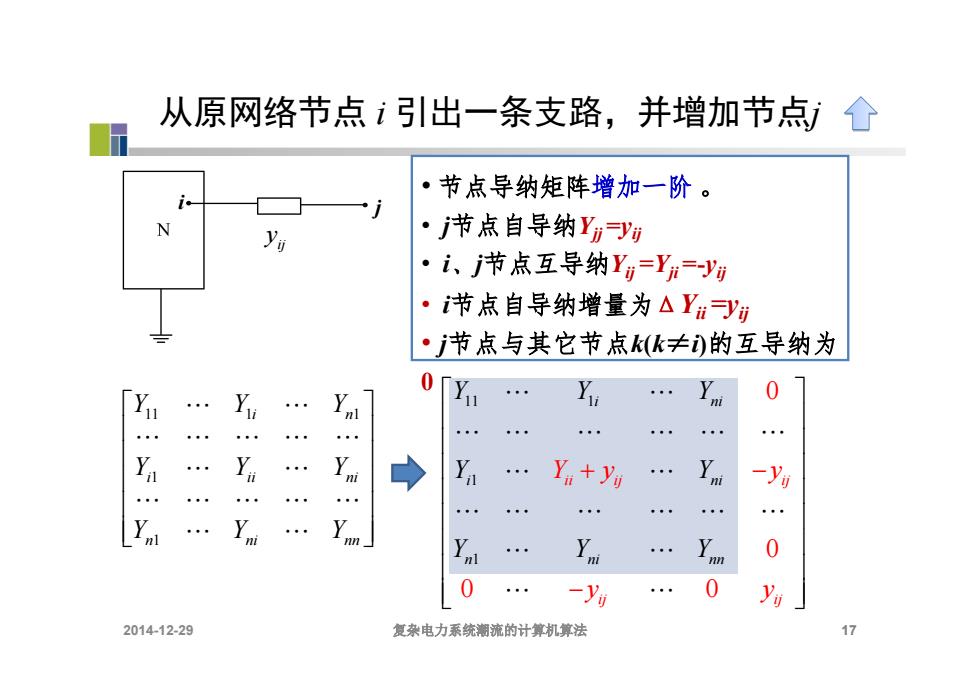
从原网络节点i引出一条支路,并增加节点)个 节点导纳矩阵增加一阶。 y ·节点自导纳yy ·i、j节点互导纳Y==y ·节点自导纳增量为△Yy ·节点与其它节点k(k≠)的互导纳为 . . 0Y 0 . → Ya . Y+yu -Yv . . . n 0 0 -Yv 0 y 2014-12-29 复杂电力系统潮流的计算机算法 17
11 1 1 1 0 0 0 0 i ni i ni n ni nn ii ij ij ij ij Y Y Y Y Y Y Y Y y y y y Y 从原网络节点 i 引出一条支路,并增加节点j 17 i j ij y • 节点导纳矩阵增加一阶 。 • j节点自导纳Yjj =yij • i、j节点互导纳Yij =Yji =-yij • i节点自导纳增量为ΔYii =yij • j节点与其它节点k(k≠i)的互导纳为 0 n ni nn i ii ni i n Y Y Y Y Y Y Y Y Y 1 1 11 1 1 2014-12-29 复杂电力系统潮流的计算机算法

在原网络节点、之间增加一条支路个 。 节点导纳矩阵阶数不变。 节点的自导纳增量△Yy。 节点j的自导纳增量△Y) i、j互导纳增量△Yi=△Y=yo 2014-12-29 复杂电力系统潮流的计算机算法 18
在原网络节点i、j之间增加一条支路 18 • 节点导纳矩阵阶数不变 。 • 节点i的自导纳增量ΔYii =yij。 • 节点j的自导纳增量ΔYjj=yij。 • i、j互导纳增量ΔYij = ΔYji = -yij。 2014-12-29 复杂电力系统潮流的计算机算法
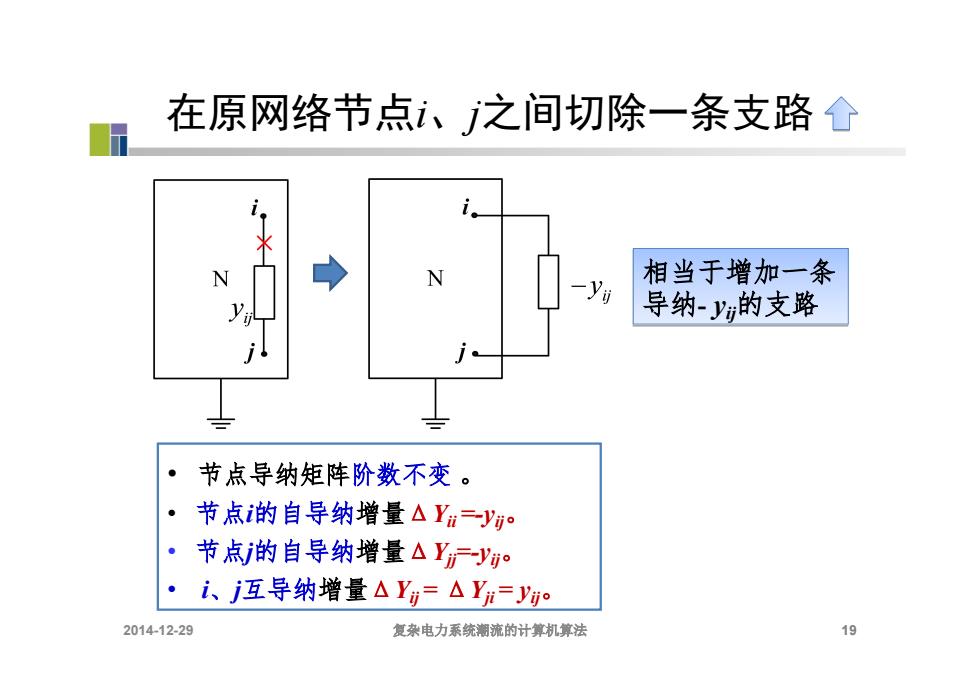
在原网络节点、之间切除一条支路个 → 相当于增加一条 导纳-y的支路 i。 ● 节点导纳矩阵阶数不变。 。 节点i的自导纳增量△Y二y 节点j的自导纳增量△Y广y。 i、互导纳增量△Y,=△Y=y 2014-12-29 复杂电力系统潮流的计算机算法 19
在原网络节点i、j之间切除一条支路 19 • 节点导纳矩阵阶数不变 。 • 节点i的自导纳增量ΔYii =-yij。 • 节点j的自导纳增量ΔYjj=-yij。 • i、j互导纳增量ΔYij = ΔYji = yij。 相当于增加一条 导纳- yij的支路 相当于增加一条 导纳- yij的支路 2014-12-29 复杂电力系统潮流的计算机算法

原网络节点i,之间的导纳由y,变为y'个 相当于先切除一条导纳为y的支路,再增加一条导纳为y'的支路。 节点导纳矩阵阶数不变。 节点的自导纳增量△Y=y'y 节点的自导纳增量△Yy'y。 i、j互导纳增量△Y,=△Y=-y'ry。 2014-12-29 复杂电力系统潮流的计算机算法 20
原网络节点i、j之间的导纳由yij变为y'ij 20 相当于先切除一条导纳为yij的支路,再增加一条导纳为 y' 相当于先切除一条导纳为yij的支路,再增加一条导纳为 y'ijij的支路。 的支路。 • 节点导纳矩阵阶数不变 。 • 节点i的自导纳增量ΔYii = y'ij-yij • 节点j的自导纳增量ΔYjj= y'ij-yij 。 • i、j互导纳增量ΔYij = ΔYji = -(y'ij-yij)。 2014-12-29 复杂电力系统潮流的计算机算法