《电路》课程教学资源（PPT课件）第十五章 电路方程的矩阵形式

电路方程的矩阵形式电路②用矩阵A]T表示矩阵形式的KVL方程。Wnl[un ] =Un2设：u / T[u]- [u z u, us us tun30- Uni + Un3Ui001-unlU2unl0Un1 -1un2U3[A] [u. ]=Un2U4u00n2u01Us0n3un3U600Un2矩阵形式的KVI[u]=[A]' [un ]返上回页下页

上 页 下 页 ②用矩阵[A] T表示矩阵形式的KVL方程。 设:     T 1 2 3 4 5 6 u = u u u u u u             = n3 n2 n1 u u u un                                 − − − = 3 2 1 n T 0 1 0 0 0 1 1 0 1 1 0 0 0 0 0 1 1 1 n n n u u u A u =                     − − − − + = 2 3 n2 1 2 1 n1 n3 n n n n n u u u u u u u u                     u u u u u u 6 5 4 3 2 1 KVL [ ] [ ] [ ]n T 矩阵形式的 u = A u 返 回

电路方程的矩阵形式电路2.回路矩阵B独立回路与支路的关联性质可以用回路矩阵B描述支路b独立回路注意每一行对应一个独立回路，[B]=l xb每一列对应一条支路7矩阵B的每一个元素定义为：支路j在回路中，且方向一致；1福b-1支路在回路冲中，且方向相反；0支路各j不在回路i中。返上回页下页

上 页 下 页 2. 回路矩阵B 独立回路与支路的关联性质可以用回路矩阵B描述。 [B]= l b 独 支路b 立 回 路 l 注意 每一行对应一个独立回路， 每一列对应一条支路。 矩阵B的每一个元素定义为： bij 1 支路 j 在回路 i 中，且方向一致； -1 支路 j 在回路 i中，且方向相反； 0 支路 j 不在回路 i 中。 返 回

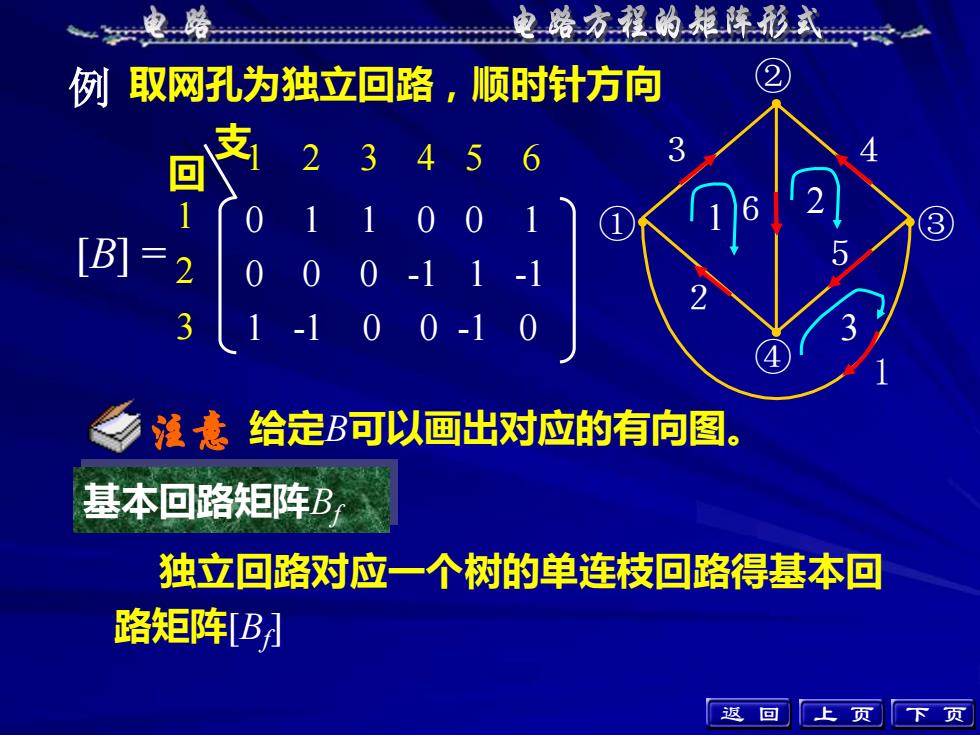
电路方程的矩阵形式电路X例取网孔为独立回路，顺时针方向支34回2761门-5[B] = 2234给定B可以画出对应的有向图注意基本回路矩阵B独立回路对应一个树的单连枝回路得基本回路矩阵[B]返上回页下页

上 页 下 页 例 1 ２ ３ ６ ５ ４ ① ② ④ 1 ③ 2 3 取网孔为独立回路，顺时针方向 给定B可以画出对应的有向图。 1 2 3 [B] = 回 支1 2 3 4 5 6 0 1 1 0 0 1 0 0 0 -1 1 -1 1 -1 0 0 -1 0 注意 基本回路矩阵Bf 独立回路对应一个树的单连枝回路得基本回 路矩阵[Bf ] 返 回

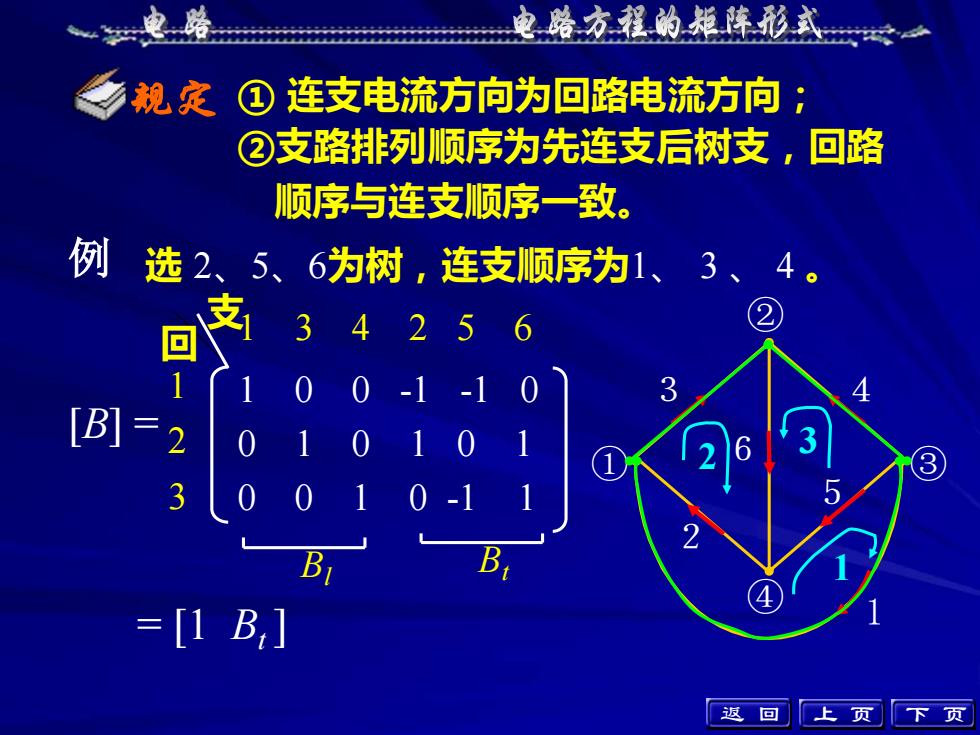
电路方程的矩阵形式电路连支电流方向为回路电流方向：规定?北②支路排列顺序为先连支后树支，回路顺序与连支顺序一致。例选 2、5、6为树,连支顺序为1、3、4支回3[B] = 2362152BB1= [1 B,]返上回页页N

②支路排列顺序为先连支后树支，回路 顺序与连支顺序一致。 上 页 下 页 规定 ① 连支电流方向为回路电流方向； 例 选 2、5、6为树，连支顺序为1、 3 、 4 。 1 ２ ３ ６ ５ ４ ① ② ④ 2 ③ 3 1 1 2 3 [B] = 回 支1 3 4 2 5 6 1 0 0 -1 -1 0 0 1 0 1 0 1 0 0 1 0 -1 1 B Bt l = [1 Bt ] 返 回

电路方程的矩阵形式电路回路矩阵[B的作用①用回路矩阵[B]表示矩阵形式的KVL方程；1个独立设[u] =[u, u, us u, u, u.]KVL方程uiuuiu3ui-uz-us[B][ u ]=u4=0Us + U, +uU2U-Us + U6UsU6矩阵形式的KVL:「BIu]= O返上回页下页

上 页 下 页 回路矩阵[B]的作用 ①用回路矩阵[B]表示矩阵形式的KVL方程； 设 [ ] [ ] u = u1 u3 u4 u2 u5 u6 ul ut [ B ][ u ]= 1 0 0 -1 -1 0 0 1 0 1 0 1 0 0 1 0 -1 1                   u u u u u u 6 5 2 4 3 1 0 4 5 6 3 2 6 1 2 5 =           − + + + − − = u u u u u u u u u l个独立 KVL方程 矩阵形式的KVL：[ B ][ u ]= 0 返 回