
电路方程的矩阵形式电路15.2关联矩阵、回路矩阵、割集矩阵1.图的矩阵表示图的矩阵表示是指用矩阵描述图的拓扑性质,即KCL和KVL的矩阵形式。有三种矩阵形式:结点支路关联矩阵二回路支路回路矩阵割集支路割集矩阵返上回页下页
15.2 关联矩阵、回路矩阵、割集矩阵 图的矩阵表示是指用矩阵描述图的拓扑性质,即 KCL和KVL的矩阵形式。有三种矩阵形式: 上 页 下 页 1. 图的矩阵表示 结点 支路 关联矩阵 回路 支路 回路矩阵 割集 支路 割集矩阵 返 回

电路方程的矩阵形式电路2.关联矩阵A用矩阵形式描述结点和支路的关联性质。n个结点b条支路的图用nxb的矩阵描述:支路b注意结点每一行对应一个结点,xbna每一列对应一条支路。n矩阵A,白的每一个元素定义为支路与结点i关联,方向背离结点;kaik=1支路与结点关联,方向指向结点;kaik=-1福1支路与结点i无关。kajk =0返上回页下页
上 页 下 页 2. 关联矩阵A 用矩阵形式描述结点和支路的关联性质。n个 结点b条支路的图用nb的矩阵描述: Aa = n b 支路b 结 点 n 每一行对应一个结点, 每一列对应一条支路。 矩阵Aa的每一个元素定义为: 注意 ajk ajk =1 支路 k 与结点 j 关联,方向背离结点; ajk= -1 支路 k 与结点 j 关联,方向指向结点; ajk =0 支路 k 与结点 j 无关。 返 回
电路方程的矩阵形式电路X支例结5636=24①532特点①每一列只有两个非零元素,一个是+1,一个是-1,A,的每一列元素之和为零②矩阵中任一行可以从其他n-1行中导出,即只有n-1行是独立的。返上回页页N
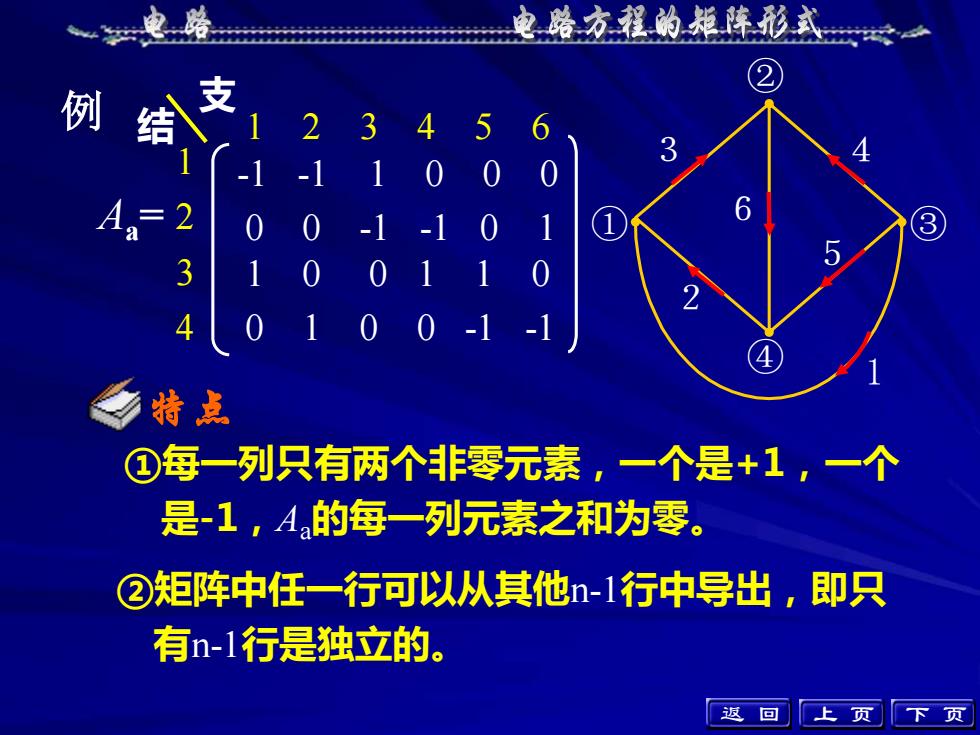
上 页 下 页 例 1 2 3 6 5 4 ① ② ④ ③ 特点 ①每一列只有两个非零元素,一个是+1,一个 是-1,Aa的每一列元素之和为零。 Aa = 1 2 3 4 1 2 3 4 5 6 支 结 -1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 1 1 0 0 1 0 0 -1 -1 ②矩阵中任一行可以从其他n-1行中导出,即只 有n-1行是独立的。 返 回
电路方程的矩阵形式电路支结6支路b00结点Aa=A,=2(n-1) ×b0n-1降阶关联矩阵A特点A的某些列只具有一个+1或一个-1,这样被划去的的列对应与划去结点相关联的一条支路。行对应的结点可以当作参考结点。返上回页N
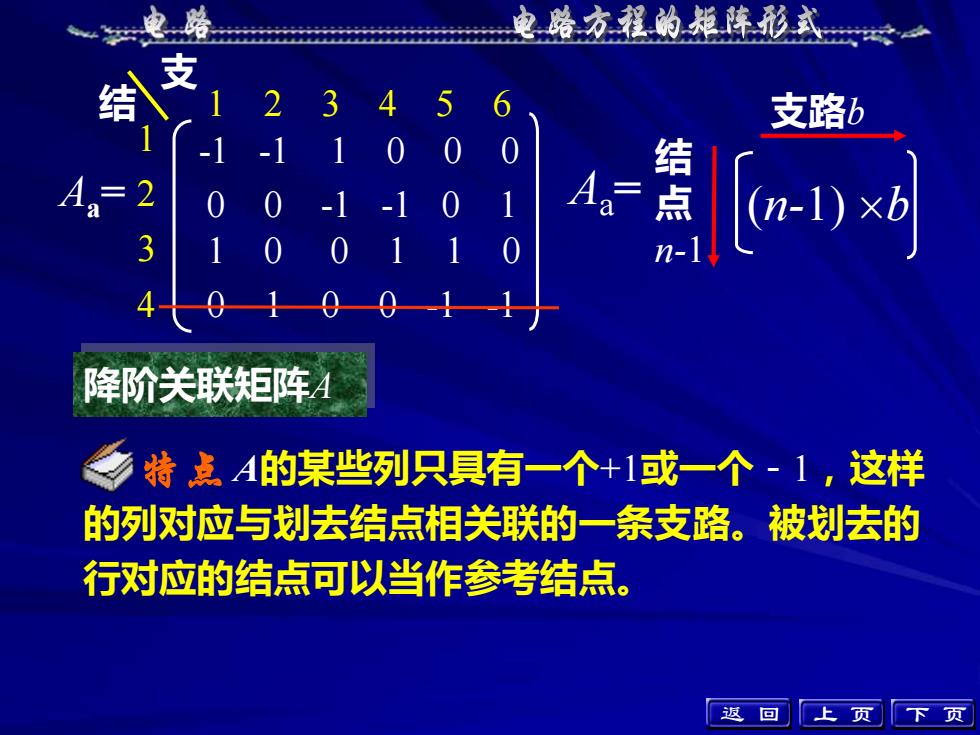
上 页 下 页 Aa = 1 2 3 4 1 2 3 4 5 6 支 结 -1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 1 1 0 0 1 0 0 -1 -1 降阶关联矩阵A 特点 A的某些列只具有一个+1或一个-1,这样 的列对应与划去结点相关联的一条支路。被划去的 行对应的结点可以当作参考结点。 Aa = (n-1) b 支路b 结 点 n-1 返 回

#电路电路方程的矩阵形式关联矩阵A的作用①用关联矩阵A表示矩阵形式的KCL方程;设:[]=[iizis]n-1个独立方程以结点④为参考结点1iiii-i-i,+i3000-1=0二00is -i4 +ic[A][ i ]=1000i+i+is1矩阵形式的KCL:Ali=0返上回页下页
上 页 下 页 关联矩阵A的作用 ①用关联矩阵A表示矩阵形式的KCL方程; 设: T 1 2 3 4 5 6 i = i i i i i i 以结点④为参考结点 [A][ i ]= -1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 0 1 0 i i i i i i 6 5 4 3 2 1 0 1 4 5 3 4 6 1 2 3 = + + − + − − + = i i i i i i i i i n-1个独立 方程 矩阵形式的KCL: [ A ][ i ]= 0 返 回