
1 国(-21-202-2k-2k+) 12 '1的 k:(I-k)月 具-2-2-2k-0-2+0-2x 2: k:(1-k)(1-2k) (-)(21-2): 21:k(1-k)(1-2k): =() 求和上限原为L,求1次导后,最低次幂应为0或1.当为偶数时 ,最低次幂为0,1-2k=0,k=2;当为奇数时,最低次幂为1 ,1-2k=1,k=(1+1)/2.所以求导后求和的上限该为[2]. 16
16 ( ) ( ) ( ) ( ) 2 2 2 0 1 1 ! 1 2 ! 2 ! ! ! l k l l l l k l l l k d l x x l dx l k l k − = − − = − ( ) ( )( ) ( ) ( ) 2 2 0 1 ! 2 2 2 2 1 2 1 2 ! ! ! l k l k l k l l k l k l k x l k l k − = − − − − − + = − ( ) ( )( ) ( )( ) ( ) ( ) 2 2 0 1 ! 2 2 2 2 1 2 1 2 ! 2 ! ! ! 2 ! l k l k l k l l k l k l k l k x l k l k l k − = − − − − − + − = − − ( ) ( ) ( ) ( ) 2 2 0 1 2 2 ! 2 ! ! ! 2 ! l k l k l k l k x l k l k l k − = − − = − − ( ) = P x l 求和上限原为l,求l 次导后,最低次幂应为0或1. 当l为偶数时 ,最低次幂为0,l – 2k = 0,k = l/2;当l为奇数时,最低次幂为1 ,l – 2k = 1,k = ( l + 1 )/2. 所以求导后求和的上限该为[ l/2]
利用罗巨格公式求P(1): 0=安(x-ヅ=旷-] =e[c-y+c*e-” 对(x-1)分别求导1-1,l-2,1-3,.次,求导后 各项均含有(x-1)项,x=1时,均为零. P0-2+y=1 17
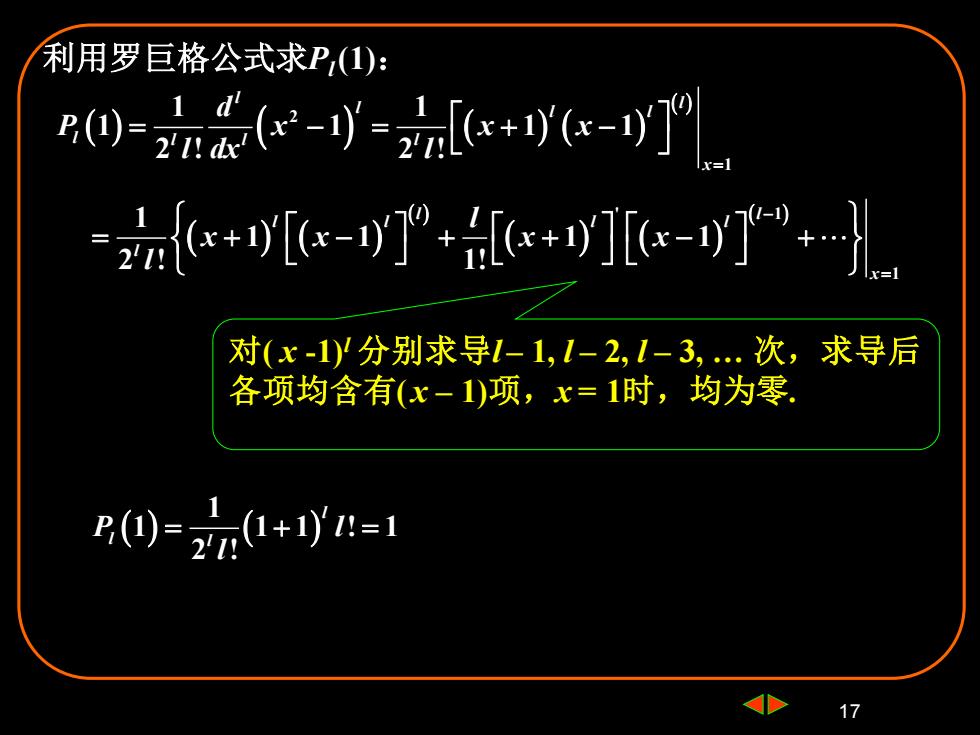
17 利用罗巨格公式求Pl (1): ( ) ( ) ( ) ( ) ( ) 2 1 1 1 1 1 1 1 2 ! 2 ! l l l l l l l l l x d P x x x l dx l = = − = + − ( ) ( ) ( ) ( ) ( ) ' 1 ( ) 1 1 1 1 1 1 2 ! 1! l l l l l l l x l x x x x l − = = + − + + − + 对( x -1)l 分别求导l – 1, l – 2, l – 3, . 次,求导后 各项均含有( x – 1)项,x = 1时,均为零. ( ) ( ) 1 1 1 1 ! 1 2 ! l l l P l l = + =

四、积分表达式 P(y)=(cos日+isin6cosp)dp,其中x=cos0. 由cos0+isin0cosp=Vcos2θ+sin20cos2p≤1 P()1. 且x=c0s0=±1时,sin0=V1-cos20=0 r0=e=1 P(-)=∫(-y'ao=(- 18
18 | | 1. ( ) P x l 且 x = = cos 1 时, 2 sin 1 cos 0 = − = ( ) 0 1 1 1 P d l = = ( ) ( ) ( ) 0 1 1 1 1 . l l P d l − = − = − 四、积分表达式 ( ) ( ) 0 1 cos sin cos , cos . l P x i d x l = + = 其中 2 2 2 由| + i cos sin cos | cos sin cos 1 = +