
第一节方差分析的基本原理和方法 均方的计算: S7= SST nk -1 Si SS, k-1 S2 SSe k(n-1)
均方的计算: ( 1) 1 1 2 2 2 − = − = − = k n SS S k SS S nk SS S e e t t T T 第一节方差分析的基本原理和方法
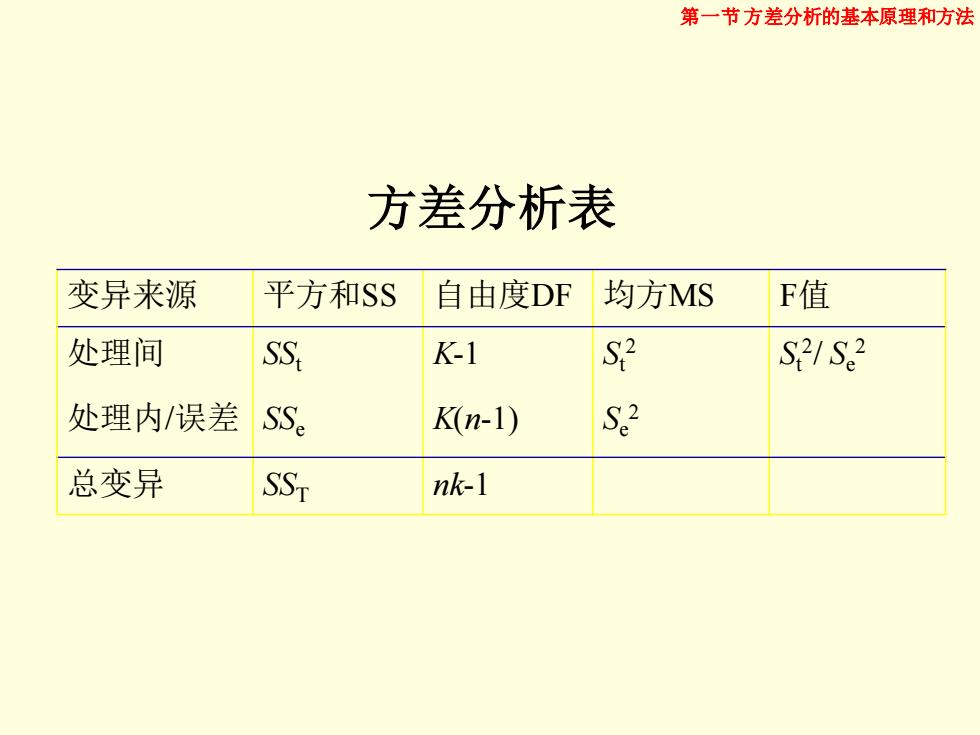
第一节方差分析的基本原理和方法 方差分析表 变异来源 平方和SS 自由度DF 均方MS F值 处理间 SS K-1 S S218 处理内/误差 SSe K(n-1) S2 总变异 SST nk-1
方差分析表 变异来源 平方和SS 自由度DF 均方MS F值 处理间 SSt K-1 St 2 St 2 / Se 2 处理内/误差 SSe K(n-1) Se 2 总变异 SST nk-1 第一节方差分析的基本原理和方法

第一节方差分析的基本原理和方法 例1:测定东小麦品种东方红3号的蛋白质含量(%)10次, 得其平均数为14.3,方差为1.621;测定农大139号的蛋白质 含量5次,得其平均数为11.7,方差为0.135。试测验东方红3 号小麦蛋白质含量的变异是否比农大139为大。 假设:H0:d12=δ22;Ha:612>δ22。 显著水平:a=0.05,DF1=9,DF2-4时,Fo.05,(9,4=6.00。 1.621 F= S2 =12.01>F594=6.00 0.135 推断:此F>F0.05,所以,P<0.05 接受H,即东方红3号小麦蛋白质含量的变异大于农大139
例1:测定东小麦品种东方红3号的蛋白质含量(%)10次, 得其平均数为14.3,方差为1.621;测定农大139号的蛋白质 含量5次,得其平均数为11.7,方差为0.135。试测验东方红3 号小麦蛋白质含量的变异是否比农大139为大。 假设:H0:δ1 2 = δ2 2 ;HA: δ1 2 > δ2 2 。 显著水平:α=0.05, DF1=9, DF2=4时, F0.05,(9,4) =6.00。 12.01 6.00 0.135 1.621 2 0.0 5,(9,4) 2 2 1 = = = F = S S F 推断:此F>F0.05,所以,P<0.05 接受HA,即东方红3号小麦蛋白质含量的变异大于农大139。 第一节方差分析的基本原理和方法

东方红3:均数:14.3,方差:1.621,n1=10 回顾测验法: 农大139:均数:11.7,方差:0.135,n2=5 分析:两样本分别来自于两个不同的总体,总体方差均为未 知,不能假设o2=0,2。可采用近似t分布两尾测验的方法。 假设:H0:41=2;HA:412© 显著水平:a=0.05。 计算;两个样本的样本容量不同,需转换自由度。 1.621/10 0.1621 k= =0.86 1.621/10+0.135/50.1621+0.0270 V= =1.48≈11 (0.862(1-0.86 10-1 5-1
分析:两样本分别来自于两个不同的总体,总体方差均为未 知,不能假设σ1 2 =σ2 2。可采用近似 t 分布两尾测验的方法。 假设:H0:μ1 = μ2;HA: μ1≠μ2。 显著水平:α=0.05。 回顾t测验法: 东方红3:均数:14.3,方差:1.621,n1=10 农大139:均数:11.7,方差:0.135,n2=5 计算;两个样本的样本容量不同,需转换自由度。 0.86 0.1621 0.0270 0.1621 1.621/10 0.135/ 5 1.621/10 = + = + k = 1.48 11 5 1 (1 0.86) 10 1 (0.86) 1 ' 2 2 = − − + − v =

计算t值: 1.6210.135 S-3= =0.435 10 5 4= 43-11.7 =5.98 0.435 查表,t0.05,1=2.301。 计算值1=5,98>t0.os,11,故P<0.05 推断:接受HA,否定Ho,即两品种蛋白质含量有 极显著差异。 在σ≠σ时的t测验,如果两个样本的样本容 量相同n1=n2n,则在t测验时,可不必进行自由 度的转换,可直接取自由度为m一1
推断:接受HA,否定H0,即两品种蛋白质含量有 极显著差异。 在σ1≠ σ2时的t 测验,如果两个样本的样本容 量相同n1=n2=n,则在 t 测验时,可不必进行自由 度的转换,可直接取自由度为n-1。 查表,t0.05,11=2.301。 计算值|t|=5.98> t0.05,11,故P<0.05 5.98 0.435 14.3 11.7 0.435 5 0.135 10 1.621 ' 1 2 = − = − = + = v x x t 计算 S t值;