第一节方差分析的基本原理和方法 1、自由度和平方和的分解 设有K组样本,每样本均具有个观察值,则该资料共有 nk个观察值,数据如下表。 表每组具个观察值的k组样本的符号表 组别 . 总和 平均 均方 1 Xu X21 X Xin T 1 S X12 Xi2 X2n T2 X2 S . . J X X Xin T S k Tk Xk S T=∑,=∑xX Xyi=1,2,.k,j-1,2,.n
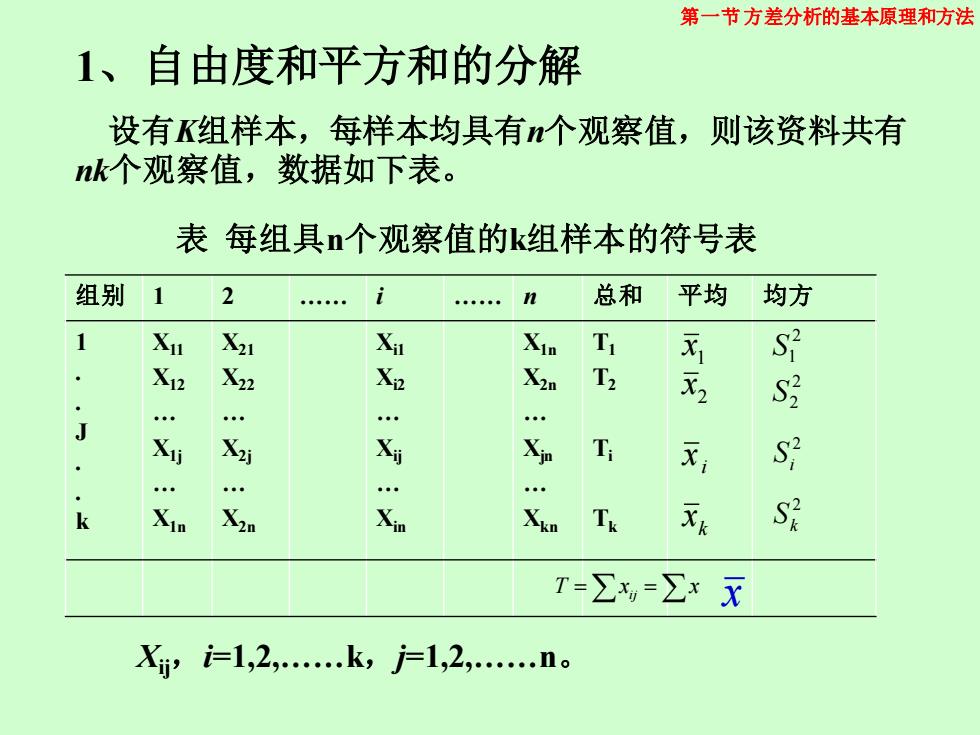
1、自由度和平方和的分解 设有K组样本,每样本均具有n个观察值,则该资料共有 nk个观察值,数据如下表。 组别 1 2 . i . n 总和 平均 均方 1 . . J . . k X11 X12 . X1j . X1n X21 X22 . X2j . X2n Xi1 Xi2 . Xij . Xin X1n X2n . Xjn . Xkn T1 T2 Ti Tk 表 每组具n个观察值的k组样本的符号表 1 x 2 x i x k x T =x =x ij x 2 1 S 2 2 S 2 i S 2 k S 第一节方差分析的基本原理和方法 Xij,i=1,2,.k,j=1,2,.n

第一节方差分析的基本原理和方法 总平方和(SS 总变异是nk个观察值的变异,故其自由度为 nk一1,平方和SS为: s,-220-Σ nk nk (T-c 式中,C称为矫正数。 nk -Σr-g-∑-c
总变异是nk个观察值的变异,故其自由度为 nk-1,平方和SST为: nk T x nk x SS x x x T 2 2 2 2 2 ( ) ( ) = ( − ) = − = − 式中,C 称为矫正数。 总平方和 (SST ) 第一节方差分析的基本原理和方法 C nk T = 2 ( ) x C nk T SS x T = − = − 2 2 2 ( )

总平方和SS的计算: 气-,-元+年-到 =26-+22X怎-0+2x- =∑(x,-x+民-x 5,=2x,-立2(x,-产+n2,- 总平方和SST=组内平方和SSe十处理平方和SSt
= = − = − + − n j i j i i n j i j x x x x x x 1 2 1 2 ( ) ( ) = = = = − + − − + − n j i n j i j i i n j i j i x x x x x x x x 1 2 1 1 2 ( ) 2( )( ) ( ) 2 1 2 (x x ) n(x x) i n j = ij − i + − = = = = = = = − = − + − k i i k i n j i j i k i n j T i j SS x x x x n x x 1 2 1 1 2 1 1 2 ( ) ( ) ( ) 总平方和SST=组内平方和SSe+处理平方和SSt 总平方和SST的计算:

第一节方差分析的基本原理和方法 上述总变异的自由度和平方和可分解为组间和组内两个 部分。组间变异即k个平均数的变异,故其自由度为k一1, 平方和SSt为: SS,=n∑(c-x)2 组内的变异为各组内观察值与组平均数的相差,故每组 具有一1个自由度,平方和为∑(s,-x)》,而总共有k组资料, 故组内自由度为k(n一1),而组内平方和SSe为: w-空s-
组内的变异为各组内观察值与组平均数的相差,故每组 具有n-1个自由度,平方和为 ,而总共有k 组资料, 故组内自由度为k(n-1),而组内平方和SSe为: 2 ( − ) ij i x x t k i T n j SSe xi j xi = SS − SS = − =1 =1 2 ( ) 第一节方差分析的基本原理和方法 上述总变异的自由度和平方和可分解为组间和组内两个 部分。组间变异即k个平均数的变异,故其自由度为k-1, 平方和 SSt 为: = − 2 SS n (x x) t i

第一节方差分析的基本原理和方法 因此,上述资料的自由度和平方和的分解式为: 总自由度=组间自由度十组内自由度 (nk-1)=(k-1)+k(n-1) 总平方和=组间平方和十组内平方和 ∑馬到=应属-区馬门
因此,上述资料的自由度和平方和的分解式为: 总自由度=组间自由度 + 组内自由度 (nk-1)=(k-1)+ k(n-1) 总平方和=组间平方和 + 组内平方和 = = = − = − + − k i n j i j i k i i n k i j x x n x x x x 1 1 2 1 2 1 2 ( ) ( ) [ ( ) ] 第一节方差分析的基本原理和方法