
Von-Neumann Minimax Theorem Von-Neumann Minimax Theorem. 器盟xAy=热盟器xA 证明(cont'd):把它们都转化为标准形式 max t min r m t- xay≤0j=1,,n ×yj r-> ay≥0 i=1,…,m ×xi m =1 Xr 〉.y=1 ×t 台 i=1 x:≥0 i=1,.,m y≥0 i=1,…,n Equality follows directly from strong duality!
Von-Neumann Minimax Theorem Von-Neumann Minimax Theorem. max #∈%! min &∈%" �'�� = min &∈%" max #∈%! �'�� 证明(cont’d):把它们都转化为标准形式 7 min � � − 2 )./ - �,) �) ≥ 0 ∀� = 1, … , � 2 ,./ - �, = 1 �, ≥ 0 ∀� = 1, … , � max � � − 2 ,./ + �,�,) ≤ 0 ∀� = 1, … , � 2 ,./ + �, = 1 �, ≥ 0 ∀� = 1, … , � × � × �) × � × �, Equality follows directly from strong duality!

Yao's Minimax Principle 一个随机算法的最坏运行时间,是它在所有输入实例中期望运行时间的最大值 试考虑这样的一个零和游戏: “算法”玩家需要从不同的算法中选择,目标是最小化运行时间 “攻击”玩家需要从不同的输入实例中选择,目标是最大化运行时间 “算法”的混合策略:随机算法 “攻击”的混合策略:输入实例的概率分布 要成功地“攻击”所有的随机算法,等价的问题是: 给出一个输入实例的概率分布,使得所有的确定性算法的期望运行时间都比较大 8
Yao’s Minimax Principle 一个随机算法的最坏运行时间,是它在所有输入实例中期望运行时间的最大值 试考虑这样的一个零和游戏: “算法”玩家需要从不同的算法中选择,目标是最小化运行时间 “攻击”玩家需要从不同的输入实例中选择,目标是最大化运行时间 “算法”的混合策略:随机算法 “攻击”的混合策略:输入实例的概率分布 要成功地“攻击”所有的随机算法,等价的问题是: 给出一个输入实例的概率分布,使得所有的确定性算法的期望运行时间都比较大 8
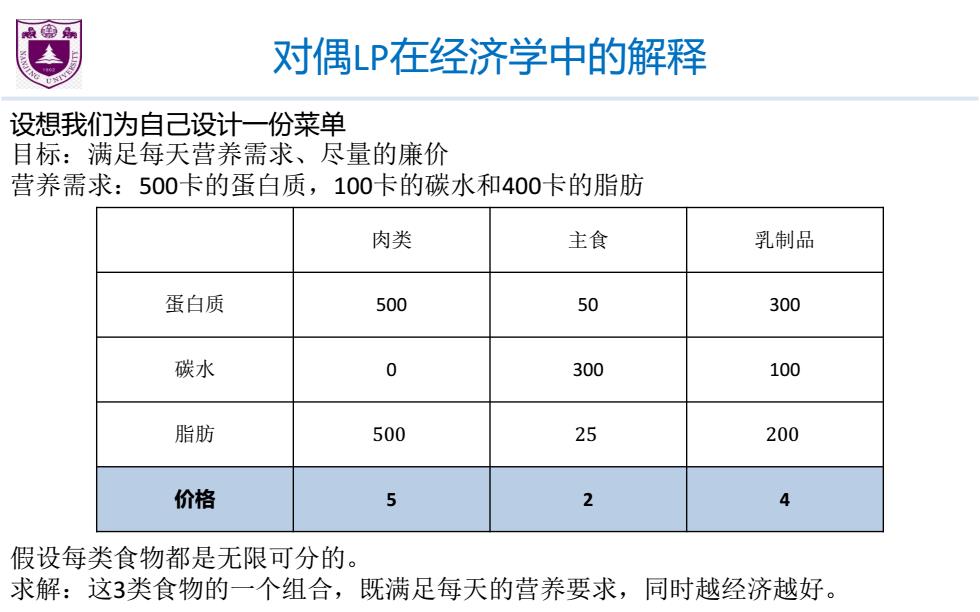
对偶LP在经济学中的解释 设想我们为自己设计一份菜单 目标:满足每天营养需求、尽量的廉价 营养需求:500卡的蛋白质,100卡的碳水和400卡的脂肪 肉类 主食 乳制品 蛋白质 500 50 300 碳水 0 300 100 脂肪 500 25 200 价格 5 2 4 假设每类食物都是无限可分的。 求解:这3类食物的一个组合,既满足每天的营养要求,同时越经济越好
对偶LP在经济学中的解释 设想我们为自己设计一份菜单 目标:满足每天营养需求、尽量的廉价 营养需求:500卡的蛋白质,100卡的碳水和400卡的脂肪 假设每类食物都是无限可分的。 求解:这3类食物的一个组合,既满足每天的营养要求,同时越经济越好。 肉类 主食 乳制品 蛋白质 500 50 300 碳水 0 300 100 脂肪 500 25 200 价格 5 2 4

对偶LP在经济学中的解释 令x:肉类,少:主食,z:乳制品,有如下的线性规划 min 5x+2y+4z (花费) s.t.500x+50y+300z≥500 (每日蛋白质要求) 0x+300y+100z≥100 (每日碳水要求) 500x+25y+200z≥400 (每日脂肪要求) x,y,z≥0. 对偶规划如下. max500a+100b+400c s.t.500a+0b+500c≤5 50a+300b+25c≤2 新产品达到肉类同样的营养的所需 300a+100b+200c≤4 花费不应该超过肉类 a,b,c≥0 否则客户只会直接购买肉类 设想一家未来的制药公司有蛋白质,碳水和脂肪三种药丸作为新产品。 应该如何为这些药丸定价?
对偶LP在经济学中的解释 设想一家未来的制药公司有蛋白质,碳水和脂肪三种药丸作为新产品。 应该如何为这些药丸定价? 新产品达到肉类同样的营养的所需 花费不应该超过肉类 否则客户只会直接购买肉类

Optimal transport Earth mover's distance(选讲) “愚公移山”距离 考虑在直线上的一座“山”{P},希望通过搬运,变成另外的形状{q} 求最小的搬运方案 rudu subject to ∑fujsqnVj ∑i≤wn 2∑-2=∑o Kantorovich(-Rubinstein)对偶性: 在最优的(经过充分博奔的)传输方案之中,“自己搬运”的开销,与“最佳外包”的开销是一样的
Earth mover’s distance (选讲) “愚公移山”距离 考虑在直线上的一座“山” {�*},希望通过搬运,变成另外的形状{�*} 求最小的搬运方案 ���� 6 � 6 � ��,���,� subject to 6 * �*,& ≤ �&, ∀� 6 & �*,& ≤ �*, ∀� 6 * 6 & �*,& = 6 * �* = 6 & �& Kantorovich(-Rubinstein) 对偶性: 在最优的(经过充分博弈的)传输方案之中,“自己搬运”的开销,与“最佳外包”的开销是一样的 Optimal transport