
3.「齐次定理和叠加定理 不次定理 3、论证齐次定理的正确性: 西 (1)设某电路仅在网孔a中有一电 (3)对网孔a有: 压源s,则其网孔方程写为: Us R12 0 安电子科技大学电路与系统多媒体室制 R11ia+R126+…+Rma=ug R22 △a R2m =K1us Raig R22ip++R2mig =0; 0 Rm2 R.mm Rmia Rm2i++Rmmia =O 因此有: (2)系数行列式: Aa=KL.us -K2 R2… R21 R22 R2m △、K1、K2为常量,它只与电路结 △= ≠0 构和电路元件参数有关,与激励无 关。 Rm Rm2 即,该电路具有唯一解。 6员 回目
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 (1)设某电路仅在网孔a中有一电 压源uS,则其网孔方程写为: 0; 0; ; 1 2 2 1 2 2 2 1 1 1 2 1 + + + = + + + = + + + = m a m b mm a a b m a a b m a s R i R i R i R i R i R i R i R i R i u (3)对网孔a有: s m mm m s m a K u R R R R u R R = = 1 2 22 2 12 1 0 0 (2)系数行列式: 0 1 2 21 22 2 11 12 1 = m m mm m m R R R R R R R R R 即,该电路具有唯一解。 因此有: s s a a u K u K i = = = 2 1 Δ、K1、K2为常量,它只与电路结 构和电路元件参数有关,与激励无 关。 第 3-6 页 前一页 下一页 返回本章目录 3、论证齐次定理的正确性: 3.1 齐次定理和叠加定理
.齐次定理和叠加定理 叠如定理 1、基本内容:对于具有唯一解的线性电路,多 32 个激动源共同作用时引起的响应(电路中各处的电 流、电压)等于各个激励源单独作用时(其它激励 源的值置零)所引起的响应之和。 子 2、举例说明: 以图(a)所示简单电路求支路电压u为 (a)两激励源共同作用时 例介绍叠加定理的含义。 学电 先对电路(),利用节点法列方程得 32 32 路与系统 18 解得u=10(V) 媒体 当电压源单独作用时,电流源 开路,如图(b)。由分压公式得 制 u'=12(V) (b)电压源单独作用时 (c)电流源单独作用时 当电流源单独作用时,电压源 短路,如图(C)。可得u”=-2(V) 可见,u=m'+ 回
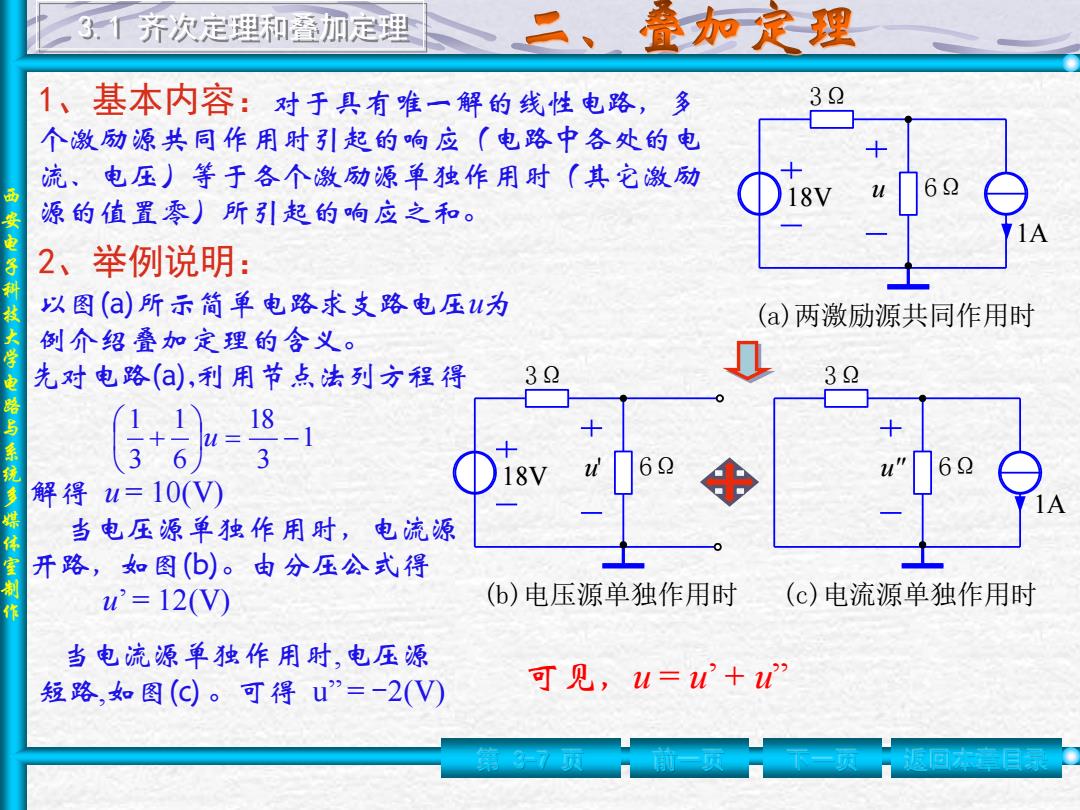
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2、举例说明: 以图(a)所示简单电路求支路电压u为 例介绍叠加定理的含义。 3Ω 6Ω 1A 18V (a)两激励源共同作用时 u 先对电路(a),利用节点法列方程得 1 3 18 6 1 3 1 = − + u 解得 u = 10(V) 当电压源单独作用时,电流源 开路,如图(b)。由分压公式得 u’ = 12(V) 3Ω 18V 6Ω (b)电压源单独作用时 u' 3Ω 6Ω 1A (c)电流源单独作用时 u" 当电流源单独作用时,电压源 短路,如图(c) 。可得 u” = -2(V) 可见,u = u’ + u” 第 3-7 页 前一页 下一页 返回本章目录 1、基本内容:对于具有唯一解的线性电路,多 个激励源共同作用时引起的响应(电路中各处的电 流、电压)等于各个激励源单独作用时(其它激励 源的值置零)所引起的响应之和。 3.1 齐次定理和叠加定理

3.齐次定理和叠加定理 、和定理 3、使用叠加定理时应注意: (1)叠加定理仅适用于线性电路求解电压和电流响应, (2)功率不能用叠加定理计算,因为功率和支路电流或 安电子科技大学电路与系统多媒体室制 支路电压是平方关条,不是线性关系。 (3)当一独立源单独作用时,其它独立源的值都应等于 零;(即,其它独立电压源短路,独立电流源开路), (4)受控源不是激励源,不能按叠加定理单独作用于电路。 (5)叠加的方式是任意的,可以一次使一个独立源单独 作用,也可以一次使几个独立源同时作用;即:可以将 独立源分成若干组分别单独作用,每组的独立源数目可 以是一个或多个
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 (1)叠加定理仅适用于线性电路求解电压和电流响应, (2)功率不能用叠加定理计算,因为功率和支路电流或 支路电压是平方关系,不是线性关系。 (3)当一独立源单独作用时,其它独立源的值都应等于 零;(即,其它独立电压源短路,独立电流源开路), (4) 受控源不是激励源,不能按叠加定理单独作用于电路。 (5)叠加的方式是任意的,可以一次使一个独立源单独 作用,也可以一次使几个独立源同时作用;即:可以将 独立源分成若干组分别单独作用,每组的独立源数目可 以是一个或多个。。 第 3-8 页 前一页 下一页 返回本章目录 3、使用叠加定理时应注意: 3.1 齐次定理和叠加定理

3.「齐次定理和叠加定理 二、春加定理 4、举例 叠加定理一般不用于具体电路的分析计算,但对于一些黑盒子电路, 西 则必须利用性质进行分析。 安电子 例如图电路,N是含有独立源的线性电路,己知 当u=6V,is=0时,开路电压4。=4V; 当u=0V,is=4A时,u。=0V; 大学 当4=-3V,is=-2A时,4。=2V; N 求当山、=3V,is=3A时的电压uo 路与 解:将激励源分为三组: 系统 ①电压源4s,②电流源is,③N内的全部独立源。 设仅由电压源山s单独作用时引起的响应为山',根据齐次定理,令山。=Ks 媒体室 仅由电流源is单独作用时引起的响应为山”,根据齐次定理,令山。”=K2is) 仅由N内部所有独立源引起的响应记为山。”,于是,根据叠加定理,有 作 4。=K14s+K2is+4。” 将己知条件代入得6K1+u。”=4,4K2+4”=0,-3K1-2K2+=2 解得,K1=1/3,K2=-1/2,u”=2 因此4。=us/3-is/2+2,当4。=3V,is=3A时的电压。=1.5V
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 叠加定理一般不用于具体电路的分析计算,但对于一些黑盒子电路, 则必须利用性质进行分析。 例 如图电路,N是含有独立源的线性电路,已知 当us = 6V,iS= 0时,开路电压uo= 4V; 当us = 0V,iS= 4A时,uo= 0V; 当us = -3V,iS= -2A时,uo= 2V; 求当us = 3V,iS= 3A时的电压uo 解:将激励源分为三组: ①电压源uS , ②电流源iS , ③N内的全部独立源。 设仅由电压源uS单独作用时引起的响应为uo ’ ,根据齐次定理,令uo ’ = K1 uS 仅由电流源iS单独作用时引起的响应为uo” ,根据齐次定理,令uo” = K2 iS; 仅由N内部所有独立源引起的响应记为uo”’ ,于是,根据叠加定理,有 uo = K1 uS+ K2 iS+ uo ”’ 将已知条件代入得 6 K1 + uo”’ = 4 ,4 K2 + uo”’ = 0 , - 3 K1 - 2 K2 + uo”’ = 2 解得, K1 =1/3, K2 = - 1/2 , uo”’ = 2 因此 uo = uS /3 - iS /2 + 2 ,当us = 3V,iS= 3A时的电压uo= 1.5V u N uo S iS 第 3-9 页 前一页 下一页 返回本章目录 4、举例 3.1 齐次定理和叠加定理
3.2春代定理ubstitution theorem 替代定理也称为置换定理,它对于简化电路的分析非常 有用。它既可用于线性电路,也可用于非线性电路。 1、替代定理基本内容:对于具有唯一解的线性或非线性电 路,若某支路的电压山或电流i已知,则该支路可用方向和大 西安电子科技大学电路与系统多媒体室制作 小与相同的电压源替代,或用方向和大小与i相同的电流源 替代,而不会影响其它各处的电流和电压。 若已知A支路电压u Ni us-U N N u 若已知A支路电流i 支路A用电压源或电流源替代后,N中的电流、电压保持不变
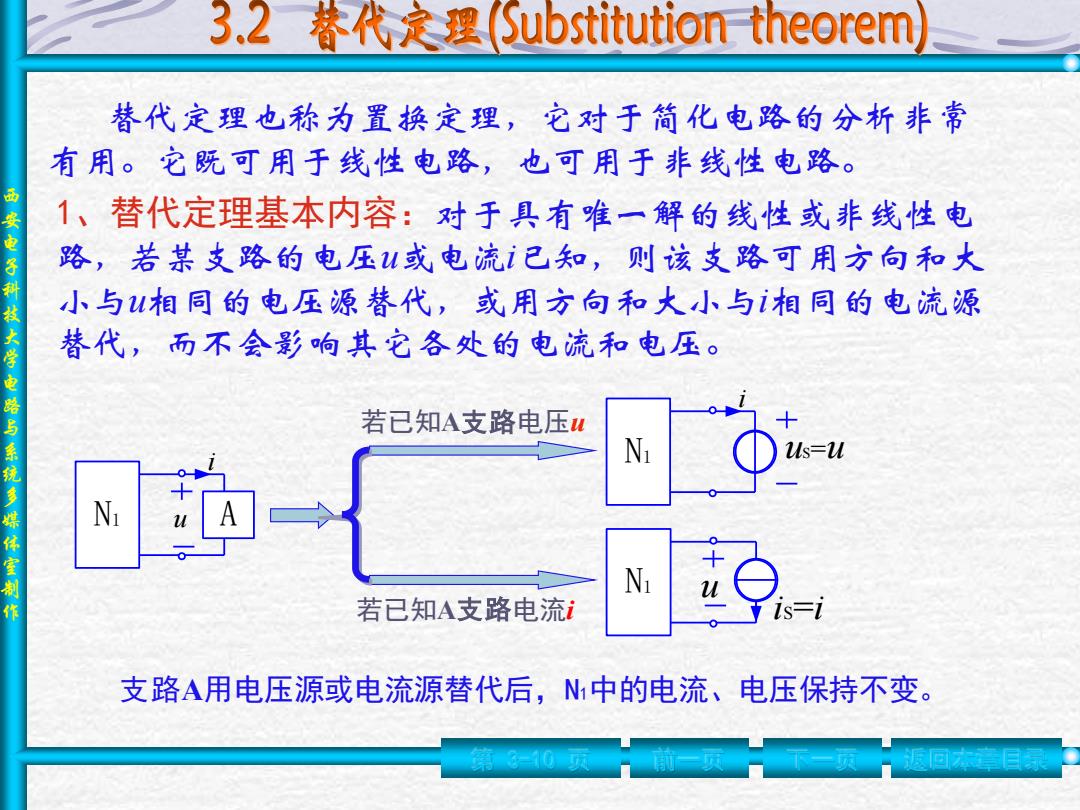
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 替代定理也称为置换定理,它对于简化电路的分析非常 有用。它既可用于线性电路,也可用于非线性电路。 若已知A支路电压u 若已知A支路电流i N1 u A i N1 uS=u i N1 u iS=i 支路A用电压源或电流源替代后,N1中的电流、电压保持不变。 第 3-10 页 前一页 下一页 返回本章目录 1、替代定理基本内容:对于具有唯一解的线性或非线性电 路,若某支路的电压u或电流i已知,则该支路可用方向和大 小与u相同的电压源替代,或用方向和大小与i相同的电流源 替代,而不会影响其它各处的电流和电压