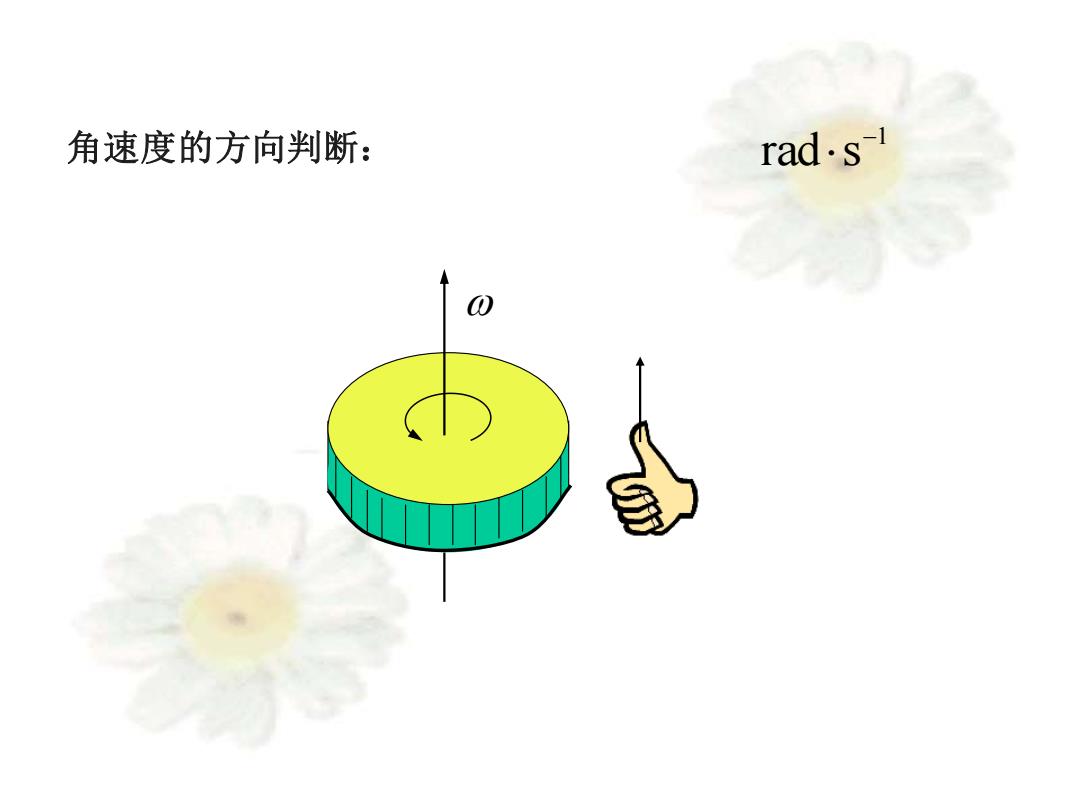
角速度的方向判断: rad.s- 0
角速度的方向判断: 1 rad s −
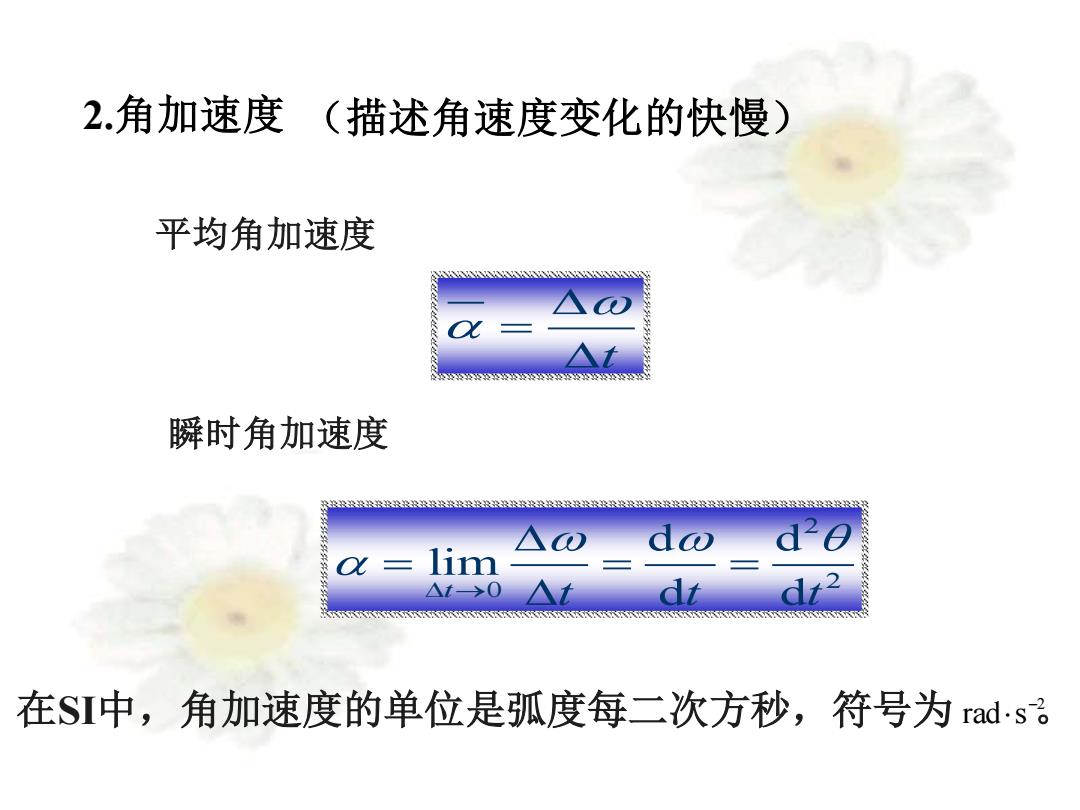
2.角加速度 (描述角速度变化的快慢) 平均角加速度 瞬时角加速度 △①) do d O光= lim △t>0Λ dt? BAXKKKXXXXN330330550563000000000030036333 在SI中,角加速度的单位是弧度每二次方秒,符号为rads
2.角加速度 (描述角速度变化的快慢) t = 2 2 0 d d lim t t t t d d → = = = 在SI中,角加速度的单位是弧度每二次方秒,符号为 。2 rad s − 平均角加速度 瞬时角加速度

角位移△0、角速度o和角加速度0,不但有 大小,而且有转向。在定轴转动的情况下,它们的转 向可用正、负值来表示。通常规定:沿逆时针转向的 △0和o取正,沿顺时针转向的△0和0取负。C的 正负号与角速度改变量△ω=0一⊙ 的正负号一 致。当刚体作加速转动时,与0同号;当刚体作 减速转动时,0与⊙,异号
注意 角位移 、角速度 和角加速度 ,不但有 大小,而且有转向。在定轴转动的情况下,它们的转 向可用正、负值来表示。通常规定:沿逆时针转向的 和 取正,沿顺时针转向的 和 取负。 的 正负号与角速度改变量 的正负号一 致。当刚体作加速转动时, 与 同号;当刚体作 减速转动时, 与 异号。 = − 0 0 0

定轴转动的特点 1)每一质点均作圆周运动,圆面为转动平面; 2)任一质点运动△0,而,均相同,但方,ā不同; 3)运动描述仅需一个坐标
1) 每一质点均作圆周运动,圆面为转动平面; 2) 任一质点运动 均相同,但 不同; 3) 运动描述仅需一个坐标 . , , a v, 定轴转动的特点

三、匀变速转动 当刚体定轴转动时,如果在任意相等的时间间隔内,角速度 的增量都是相等的,这种变速转动叫做匀变速转动。 角加速度 aconst 角速度 0=00+0t 角位移 △0=o,t+二at2 2 角位置 0=0+o,t+at2 2 质点匀变速直线运动 刚体绕定轴作匀变速转动 v-vo +at )=)。+Oxt x=xo +vot+at2 0=0。+D,t+30t2 v2=v+2a(x-xo)o2=+2ax(0-0,)
三、匀变速转动 当刚体定轴转动时,如果在任意相等的时间间隔内,角速度 的增量都是相等的,这种变速转动叫做匀变速转动。 角加速度 =const 角速度 t =0 + 角位移 2 0 2 1 = t + t 角位置 2 0 0 2 1 = + t + t 质点匀变速直线运动 刚体绕定轴作匀变速转动 = + at v v0 2 2 1 x = x0 + v0 t + at 2 ( ) 0 2 0 2 v = v + a x − x = +t 0 2 ( ) 0 2 0 2 = + − 2 2 1 0 0 = + t + t