四、角量和线量的关系 s=ro ds d(r8) )= =r0 X dt dt dv d(ro) 0= =ra dt dt v2_ (ro)=ro' 可见,八aan都与r成正比
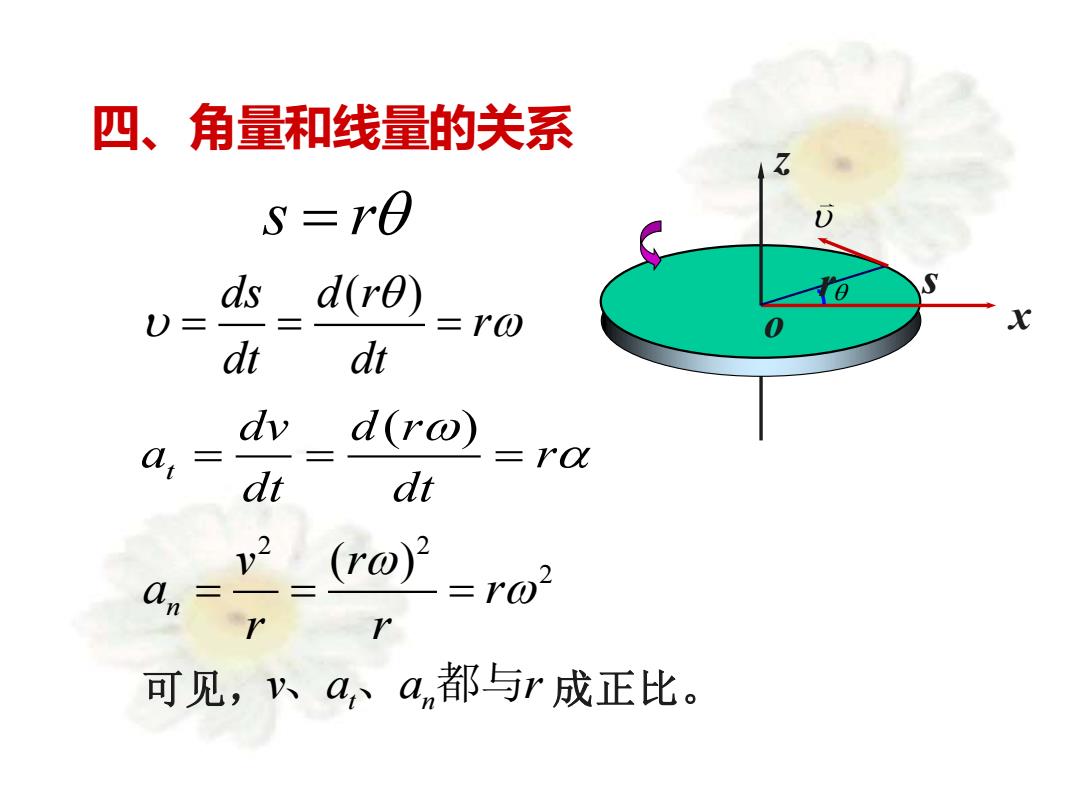
四、角量和线量的关系 s r = ds d r( ) r dt dt = = = ( ) t dv d r a r dt dt = = = 2 2 2 ( ) n v r a r r r = = = o x z r s 可见, v a a r 、 t n 、 都与 成正比

例3-1 已知刚体转动的运动方程为 0=At+Bt-Ct 在上式中,A、B、C都为常量。求:(1)角速度; (2)角加速度。 解:()由角速度定义式,得 do 0= =A+3Bt2-4Ct dt (2)由角加速度定义式,得 dω OX =6Bt-12Ct2 dt
例3-1 已知刚体转动的运动方程为 3 4 = + − At Bt Ct 在上式中,A、B、C都为常量。求:(1)角速度; (2)角加速度。 解: (1)由角速度定义式,得 d 2 3 3 4 d θ ω A Bt Ct t = = + − (2) 由角加速度定义式,得 d 2 6 12 d ω Bt Ct t = = −