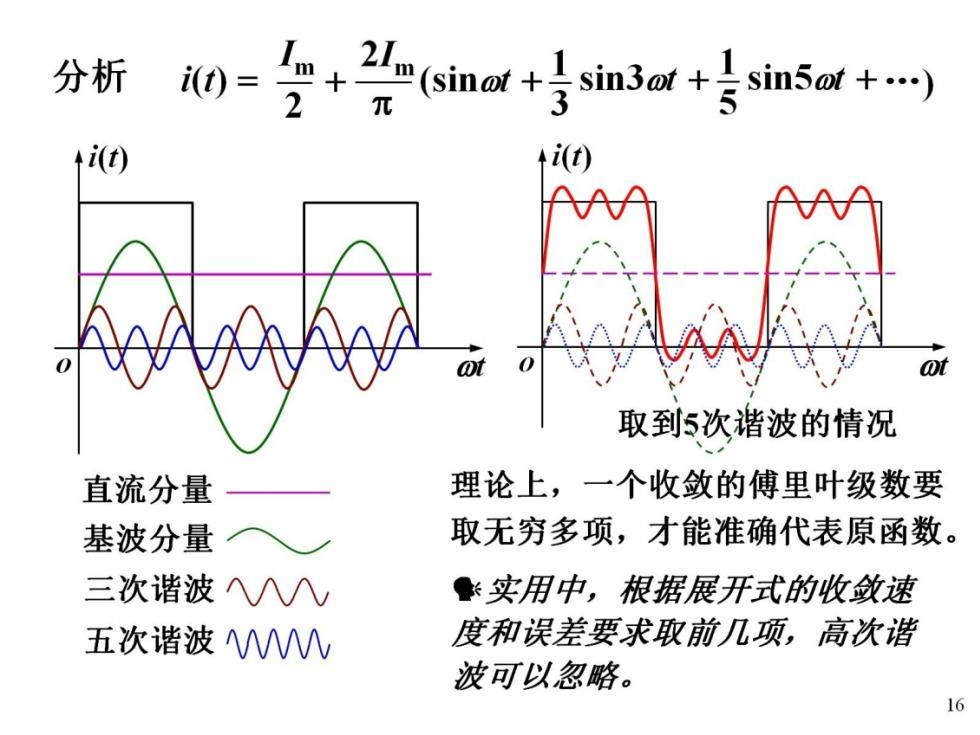
分析 0=子+2头(+s号n+号sn5a- i(t +i(t) 取到5次谐波的情况 直流分量 理论上,一个收敛的傅里叶级数要 基波分量 取无穷多项,才能准确代表原函数。 三次谐波Av ●实用中,根据展开式的收敛速 五次谐波W 度和误差要求取前几项,高次谐 波可以忽略。 16

§13-3有效值、平均值和平均功率 5回忆三角函数的性质(k为整数,下同) ①sin、cos在一个周期 ③正交性质(kq) 内的积分为0: 2元 2π coskot sinqot d(or)=0 ∫os(aw0=0 0 coskax cosqax d() 2元 ②sin2、cos2在一个周 期内的积分为π 2元 2 sinkot singot d(@r)=0 cos2kord(o0)=元 17