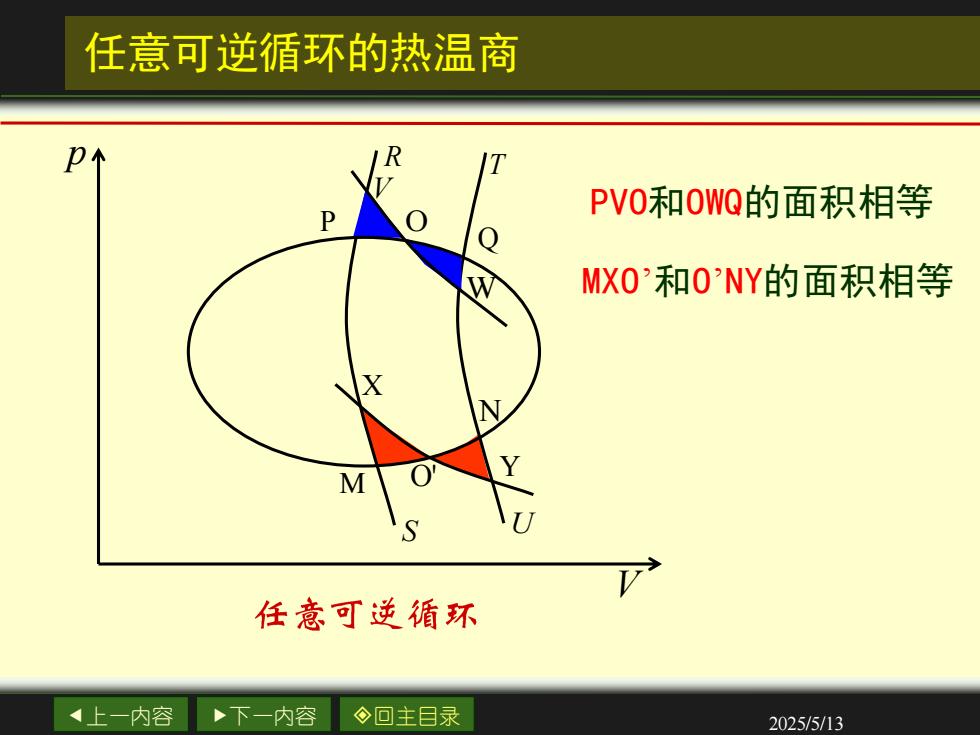
任意可逆循环的热温商 PV0和0WQ的面积相等 MX0和0NY的面积相等 任意可逆循环 上一内容 下一内容 ◇回主目录 2025/5/13
上一内容 下一内容 回主目录 2025/5/13 任意可逆循环的热温商 p V P Q M N X O' Y T U R S O V W PVO和OWQ的面积相等 MXO’和O’NY的面积相等
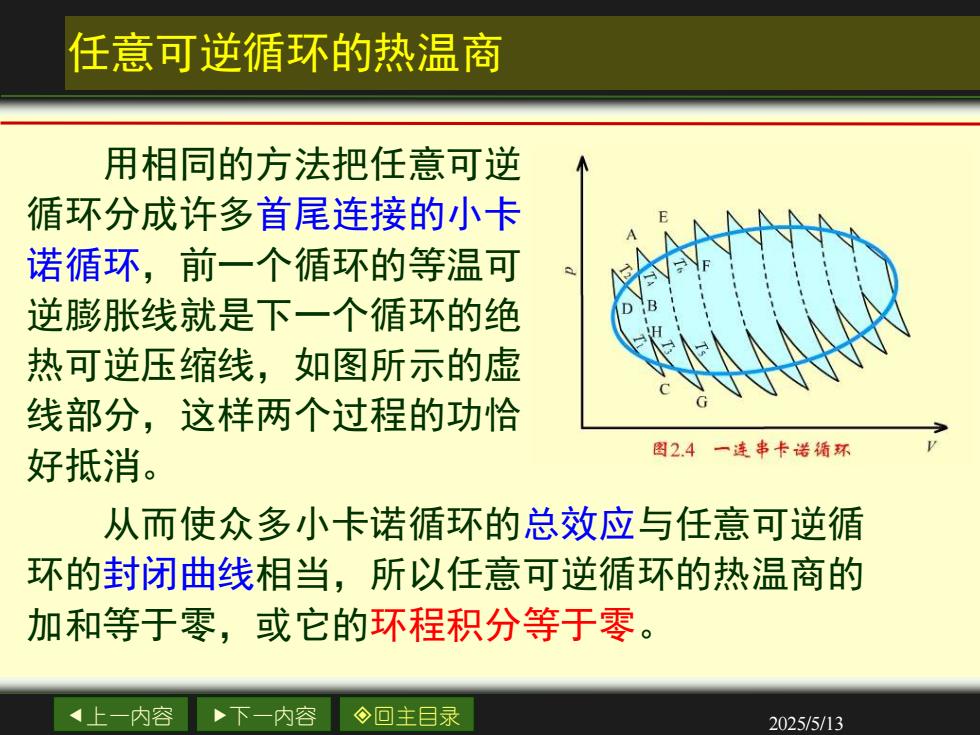
任意可逆循环的热温商 用相同的方法把任意可逆 循环分成许多首尾连接的小卡 诺循环,前一个循环的等温可 逆膨胀线就是下一个循环的绝 热可逆压缩线,如图所示的虚 线部分,这样两个过程的功恰 好抵消。 图2.4一连串卡诺循环 从而使众多小卡诺循环的总效应与任意可逆循 环的封闭曲线相当,所以任意可逆循环的热温商的 加和等于零,或它的环程积分等于零。 4上一内容 下一内容 ◇回主目录 2025/5/13
上一内容 下一内容 回主目录 2025/5/13 任意可逆循环的热温商 用相同的方法把任意可逆 循环分成许多首尾连接的小卡 诺循环,前一个循环的等温可 逆膨胀线就是下一个循环的绝 热可逆压缩线,如图所示的虚 线部分,这样两个过程的功恰 好抵消。 从而使众多小卡诺循环的总效应与任意可逆循 环的封闭曲线相当,所以任意可逆循环的热温商的 加和等于零,或它的环程积分等于零
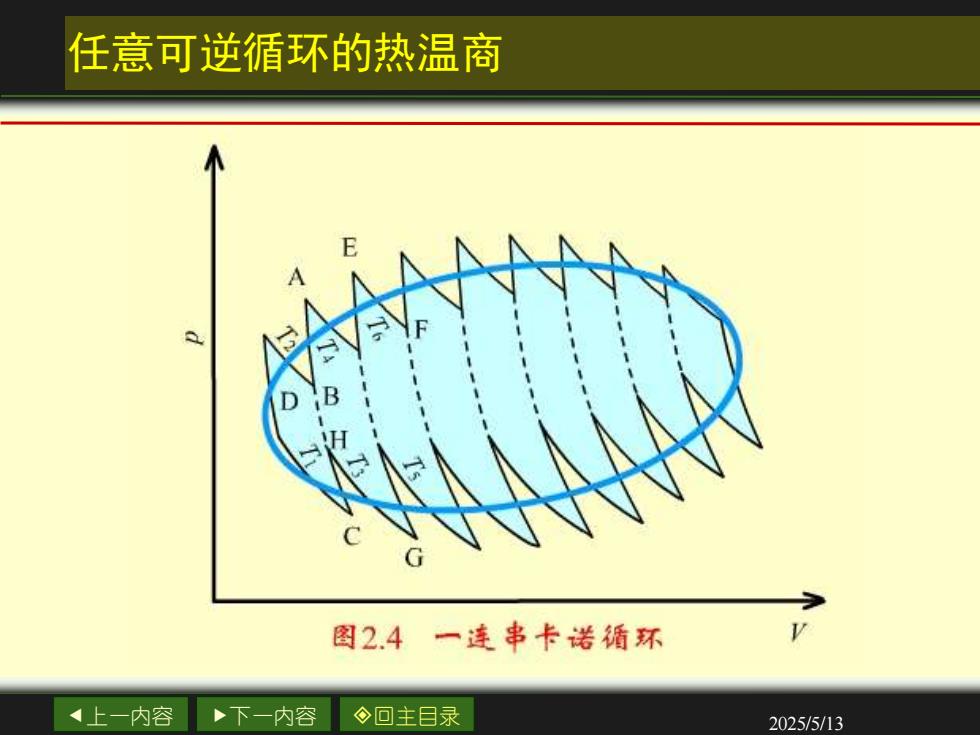
任意可逆循环的热温商 图2.4一连串卡诺循环 上一内容 下一内容 ◇回主目录 2025/5/13
上一内容 下一内容 回主目录 2025/5/13 任意可逆循环的热温商

熵的引出 用一闭合曲线代表任意可逆循环。 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: f9.=0 R 可分成两项的加和 R号+(9,=0 B 任意可逆循环 4上一内容 下一内容 ◇回主目录 2025/5/13
上一内容 下一内容 回主目录 2025/5/13 熵的引出 用一闭合曲线代表任意可逆循环。 R ( ) 0 Q T = 1 2 B A R R A B ( ) ( ) 0 Q Q T T + = 可分成两项的加和 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式:

熵的引出 移项得: A 9=9 R R 说明任意可逆过程的热温 商的值决定于始终状态,而 与可逆途径无关,这个热温 B 商具有状态函数的性质。 任意可逆过程 上一内容 下一内容 ◇回主目录 2025/5/13
上一内容 下一内容 回主目录 2025/5/13 熵的引出 说明任意可逆过程的热温 商的值决定于始终状态,而 与可逆途径无关,这个热温 商具有状态函数的性质。 移项得: 1 2 B B R R A A ( ) ( ) Q Q T T = 任意可逆过程