
Department of Computer Science and Technology,Nanjing Universit 图中的匹配 ·匹配(边独立集):互不相邻的边的集合 ·M饱和点:M中各边的端点 匹配数 匹配数 β1=3 B1=4 极大匹配 完美匹配 最大匹配 ○M饱和点 ●M-饱和点 June 2016
June 2016 6 Department of Computer Science and Technology, Nanjing University 图中的匹配 匹配(边独立集):互不相邻的边的集合 M-饱和点:M中各边的端点 匹配数 1=3 匹配数 1=4 极大匹配 最大匹配 完美匹配 M-饱和点 M-饱和点
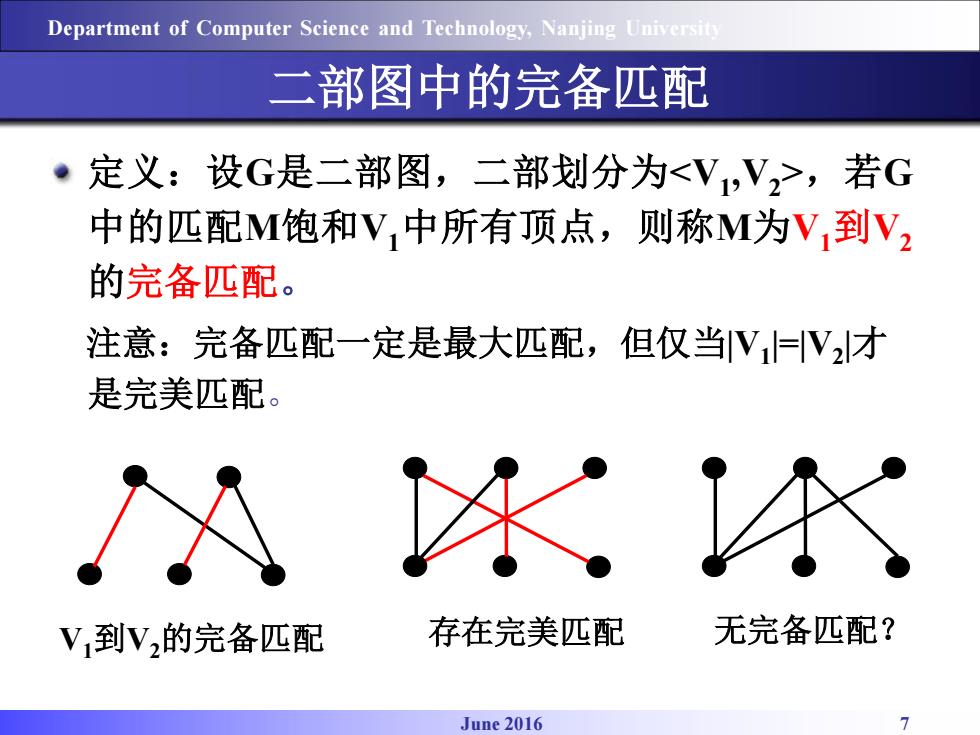
Department of Computer Science and Technology,Nanjing University 二部图中的完备匹配 定义:设G是二部图,二部划分为<V,V2>,若G 中的匹配M饱和V,中所有顶点,则称M为V到V2 的完备匹配。 注意:完备匹配一定是最大匹配,但仅当V=V,才 是完美匹配。 冰 V到V的完备匹配 存在完美匹配 无完备匹配? June 2016 7
June 2016 7 Department of Computer Science and Technology, Nanjing University 二部图中的完备匹配 定义:设G是二部图,二部划分为<V1 ,V2 >,若G 中的匹配M饱和V1中所有顶点,则称M为V1到V2 的完备匹配。 注意:完备匹配一定是最大匹配,但仅当|V1 |=|V2 |才 是完美匹配。 V1到V2的完备匹配 存在完美匹配 无完备匹配?
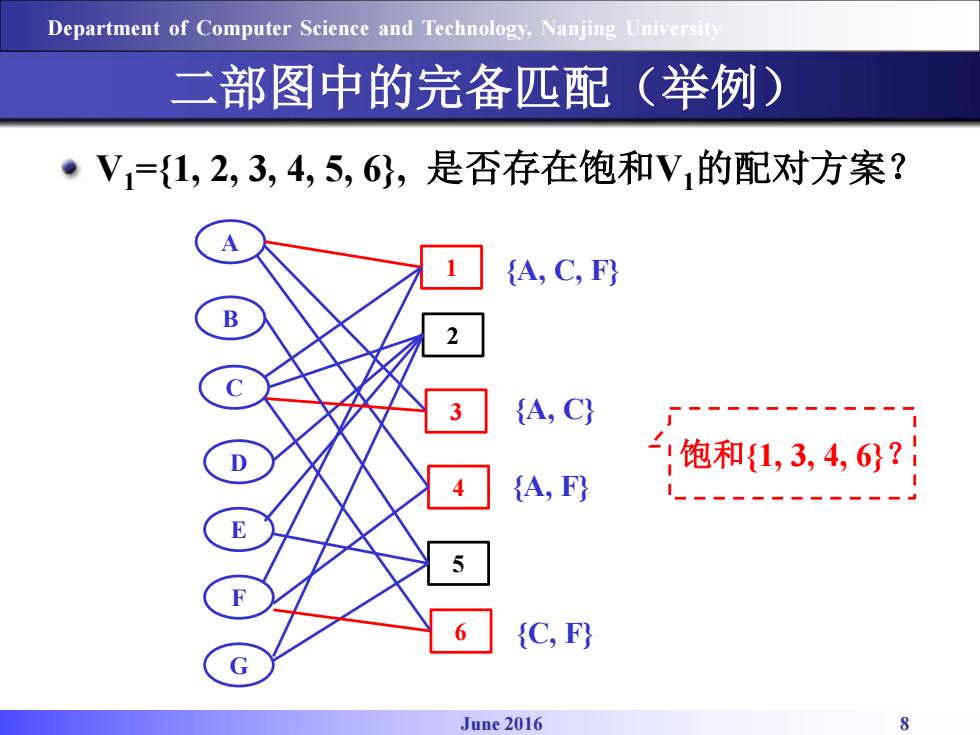
Department of Computer Science and Technology,Nanjing Universit 二部图中的完备匹配(举例) ·V={1,2,3,4,5,6,是否存在饱和V的配对方案? (A,C,F) 2 {A,C} :饱和{1,3,4,6? 4 (A,F) 5 6 (C,F) June 2016
June 2016 8 Department of Computer Science and Technology, Nanjing University 二部图中的完备匹配(举例) V1={1, 2, 3, 4, 5, 6}, 是否存在饱和V1的配对方案? A 1 B 2 C 3 D 4 E 5 F 6 G {A, C, F} {A, C} {A, F} {C, F} 饱和{1, 3, 4, 6}?

Department of Computer Science and Technology,Nanjing University Hal定理 Hall定理(1935,Marriage Theorem) 设二部图G=<V1,V2,E>,则G有V到V2的完备匹配分 对于任意的AsV1,有N(A)川≥A| ·证明.必要性易证,下证充分性(使用强归纳法)。 如果V1=1,充分性命题显然成立。 假设当V1k(k≥1)时充分性命题均成立,要证:当 V=k+1时充分性命题也成立。分二种情形来证明。 ()对V的任意真子集A,N(A)川>|A (2)存在V的一个真子集A',N(A")川=|A'I June 2016 9
June 2016 9 Department of Computer Science and Technology, Nanjing University Hall定理 Hall定理(1935, Marriage Theorem) 设二部图G=<V1 , V2 , E>, 则G有V1到V2的完备匹配 对于任意的 A V1 ,有 |N(A)| |A | 证明. 必要性易证,下证充分性(使用强归纳法)。 如果 |V1 |=1, 充分性命题显然成立。 假设当|V1 |k (k 1) 时充分性命题均成立, 要证:当 |V1 |=k+1时充分性命题也成立。分二种情形来证明。 (1)对V1的任意真子集A , |N(A)| | A | (2)存在 V1的一个真子集A', |N(A')| = | A' |

Department of Computer Science and Technology,Nanjing Universit Hall定理 ·归纳证明. 1)对V的任意真子集A,N(A)川>|A 任取一个顶点v∈V,任取w∈N(v). H=G-{V,w}是一个二部图(非空) H满足归纳假设的条件,从而 H有V1-v}到V2-{w的完备匹配. 这个匹配加上边(y,w)构成G的从 V到V,的完备匹配. June 2016
June 2016 10 Department of Computer Science and Technology, Nanjing University Hall定理 H满足归纳假设的条件, 从而 H有V1 -{v}到V2 -{w}的完备匹配. 这个匹配加上边(v, w)构成G的从 V1到V2的完备匹配. v w 归纳证明. (1)对V1的任意真子集A , |N(A)| | A | 任取一个顶点v V1 , 任取wN({v}). H=G-{v, w}是一个二部图(非空)