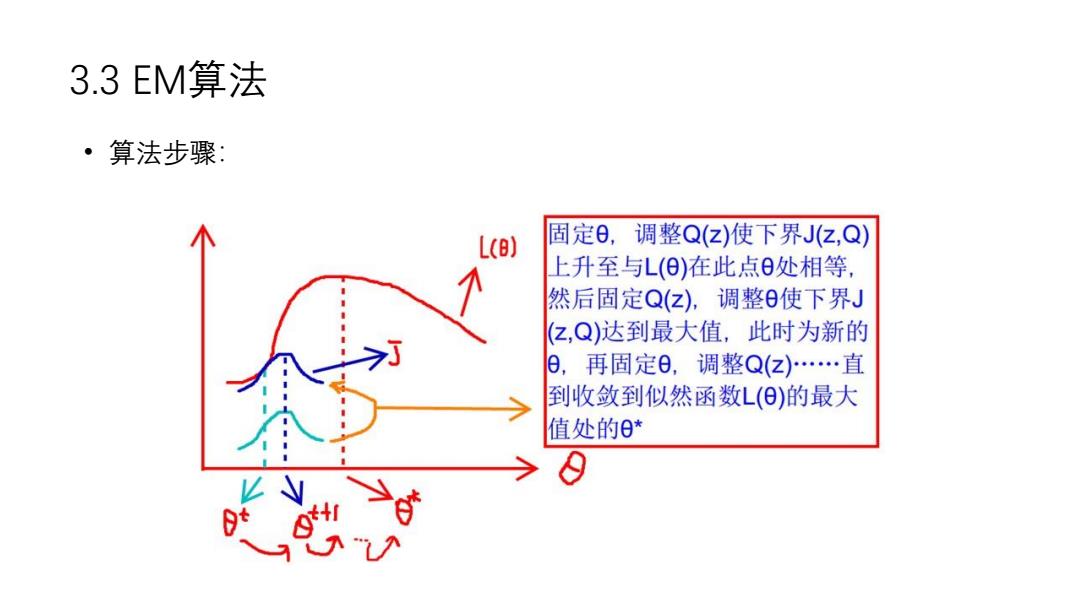
3.3EM算法 ·算法步骤: L(】 固定0,调整Q(z)使下界J(z,Q) 上升至与L(旧)在此点日处相等, 然后固定Q(z),调整0使下界J (z,Q)达到最大值,此时为新的 日,再固定0,调整Q(2)…直 到收敛到似然函数L()的最大 值处的*
3.3 EM算法 • 算法步骤:
3.3EM算法的另一种解释 ·定义J: 1009u:s Q(20 z( ·块坐标上升法(Block Coordinate ascent): ·E步:固定0,优化Q ·M步:固定Q,优化0 ·交替将极值推向最大 0.s
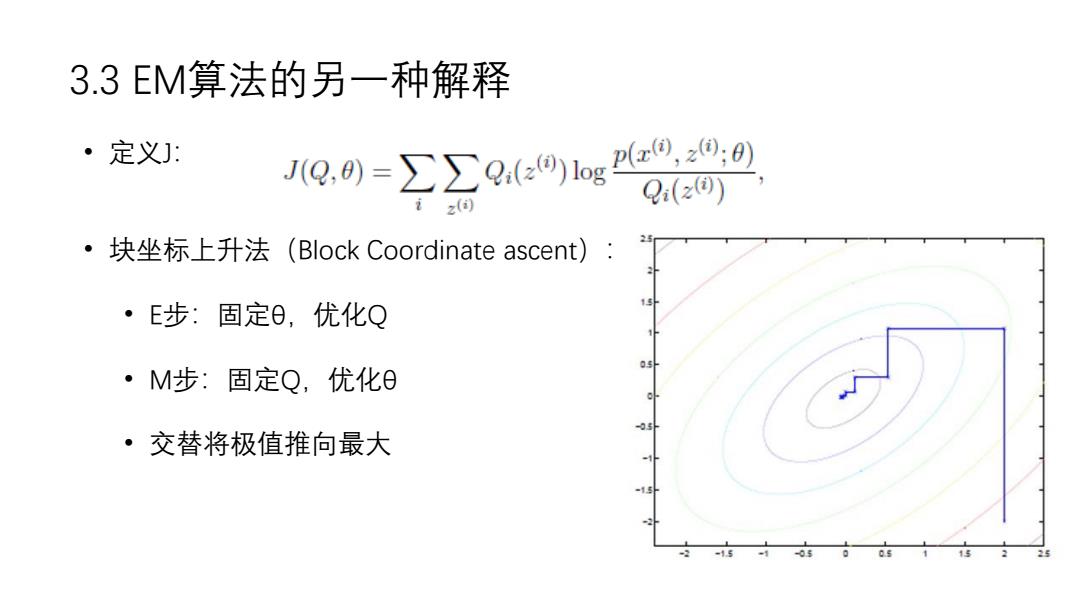
3.3 EM算法的另一种解释 • 定义J: • 块坐标上升法(Block Coordinate ascent): • E步:固定θ,优化Q • M步:固定Q,优化θ • 交替将极值推向最大
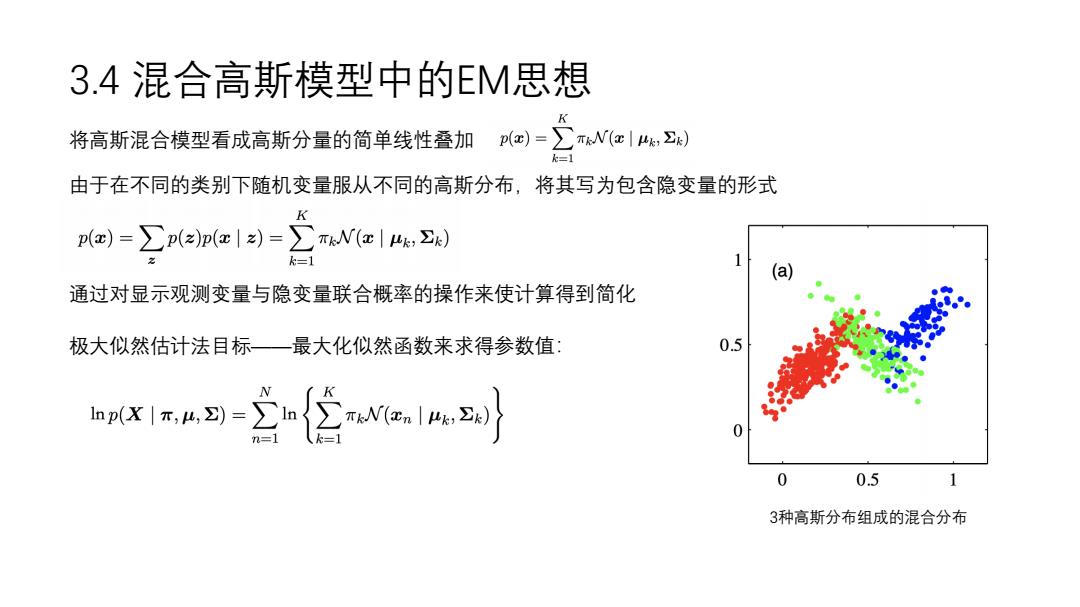
3.4混合高斯模型中的EM思想 将高斯混合模型看成高斯分量的简单线性叠加 pl=∑Nc4,2) 由于在不同的类别下随机变量服从不同的高斯分布,将其写为包含隐变量的形式 K p)=∑p(epez)=∑Ne|4e,2) (a 通过对显示观测变量与隐变量联合概率的操作来使计算得到简化 极大似然估计法目标一最大化似然函数来求得参数值: 0.5 x4习-立n{官MeA刘} 0 0.5 3种高斯分布组成的混合分布
3.4 混合高斯模型中的EM思想 将高斯混合模型看成高斯分量的简单线性叠加 由于在不同的类别下随机变量服从不同的高斯分布,将其写为包含隐变量的形式 通过对显示观测变量与隐变量联合概率的操作来使计算得到简化 3种高斯分布组成的混合分布 极大似然估计法目标——最大化似然函数来求得参数值: