
一:受控源:大小受其它支路iu控制的电源(非独立源) 说明:*受控源特点:非独立 Ic=BIb *例 Ib 二:受控源分类: 电压控制电压源VCVS 电压源 电流控制电压源CCVS 11 受控源 电压控制电流源VCCS 电流源 电流控制电流源CCCS 说明:*符号 *u.B无量纲下Qgs线性受控源4.B.rg均为常数 独立源一激励 *作用 受控源一反映某支路i.u对另一支路i.u的控制作用 *若控制量(.u)为零,则受控源大小也为零 §1-9基尔霍夫定律 一:几个名词 1、支路:电路中每一个二端元件 说明:*流进同一电流的一个分支 *例:3个支路 *支路方向(支路电流方向且支路u为关联参考方向) 2、节点一一支路的连接点 说明:*例:P29n=5b=8 3、回路:由支路构成的闭合路径 说明:◆回路可由闭合支路序列表示 *回路可由闭合节点序列表示 *但闭合节点序列不一定表示回路 4、网孔:内部不含支路的回路 5、两类约束:
11 一:受控源:大小受其它支路 i.u 控制的电源〈非独立源〉 说明:*受控源特点:非独立 *例 二:受控源分类: 说明:* 符号 * u.β无量纲 r-Ω g-s 线性受控源 ..r.g 均为常数 *作用 独立源—激励 受控源—反映某支路i.u对另一支路i.u的控制作用 *若控制量(i.u)为零,则受控源大小也为零 §1-9 基尔霍夫定律 一:几个名词 1、支路:电路中每一个二端元件 说明:* 流进同一电流的一个分支 *例:3 个支路 *支路方向(支路电流方向且支路 i.u 为关联参考方向) 2、节点——支路的连接点 说明:*例:P29 n=5 b=8 3、回路:由支路构成的闭合路径 说明:*回路可由闭合支路序列表示 *回路可由闭合节点序列表示 *但闭合节点序列不一定表示回路 4、网孔:内部不含支路的回路 5、两类约束: 电压控制电压源VCVS 电压源 电流控制电压源CCVS 受控源 电压控制电流源VCCS 电流源 电流控制电流源CCCS
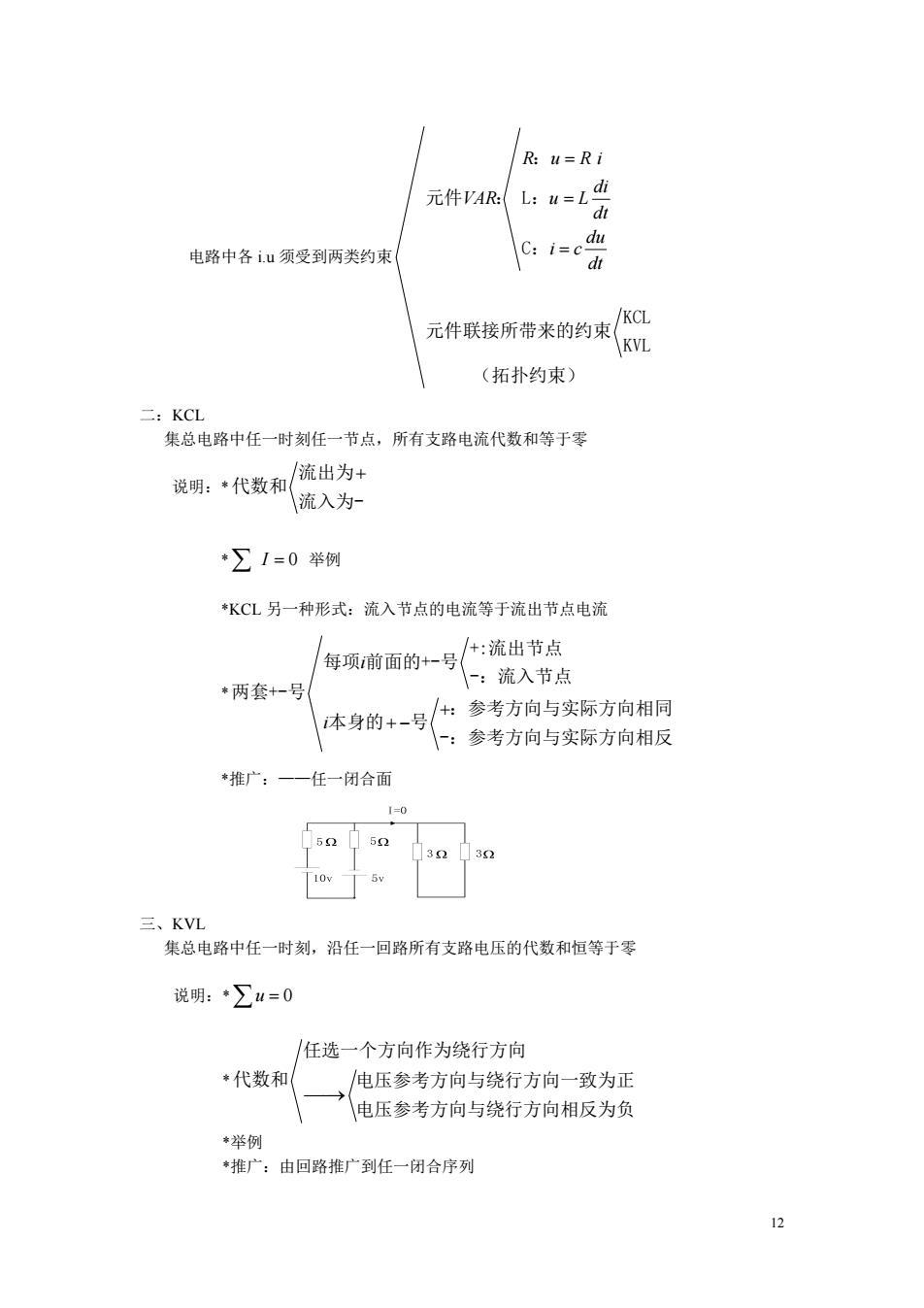
R:u=Ri 元件VAR L: u=1di dt C:i=c du 电路中各i.u须受到两类约束 dt KCL 元件联接所带来的约束 KVL (拓扑约束) 二:KCL 集总电路中任一时刻任一节点,所有支路电流代数和等于零 流出为+ 说明:*代数和 流入为 *∑1=0举例 *KCL另一种形式:流入节点的电流等于流出节点电流 每项前面的+-号 +:流出节点 -: 流入节点 *两套+-号 +: 参考方向与实际方向相同 本身的+一号 参考方向与实际方向相反 *推广:一一任一闭合面 1=0 52 5 2 5v 三、KVL 集总电路中任一时刻,沿任一回路所有支路电压的代数和恒等于零 说明:◆∑4=0 任选一个方向作为绕行方向 *代数和 电压参考方向与绕行方向一致为正 电压参考方向与绕行方向相反为负 *举例 *推广:由回路推广到任一闭合序列 12
12 电路中各 i.u 须受到两类约束 R u R i di VAR u L dt du i c dt : 元件 : L: C: KCL 元件联接所带来的约束 KVL (拓扑约束) 二:KCL 集总电路中任一时刻任一节点,所有支路电流代数和等于零 说明:* 流出为 代数和 流入为- * I 0 举例 *KCL 另一种形式:流入节点的电流等于流出节点电流 * i i +:流出节点 每项 前面的+-号 -:流入节点 两套+-号 :参考方向与实际方向相同 本身的 号 -:参考方向与实际方向相反 *推广:——任一闭合面 三、KVL 集总电路中任一时刻,沿任一回路所有支路电压的代数和恒等于零 说明:*u 0 * 任选一个方向作为绕行方向 代数和 电压参考方向与绕行方向一致为正 电压参考方向与绕行方向相反为负 *举例 *推广:由回路推广到任一闭合序列

沿着任何一个闭合序列前一个节点与后一个节点之间的全部电压代数和恒等于零。 U3+U34+U41=0 U3=U3-U4 四:KCL、KVL应用举例 P33、例1-1 补充: 3
13 沿着任何一个闭合序列前一个节点与后一个节点之间的全部电压代数和恒等于零。 四: KCL 、KVL 应用举例 P33、例 1-1 补充: 13 34 41 U U U 0 U13 U3 U4
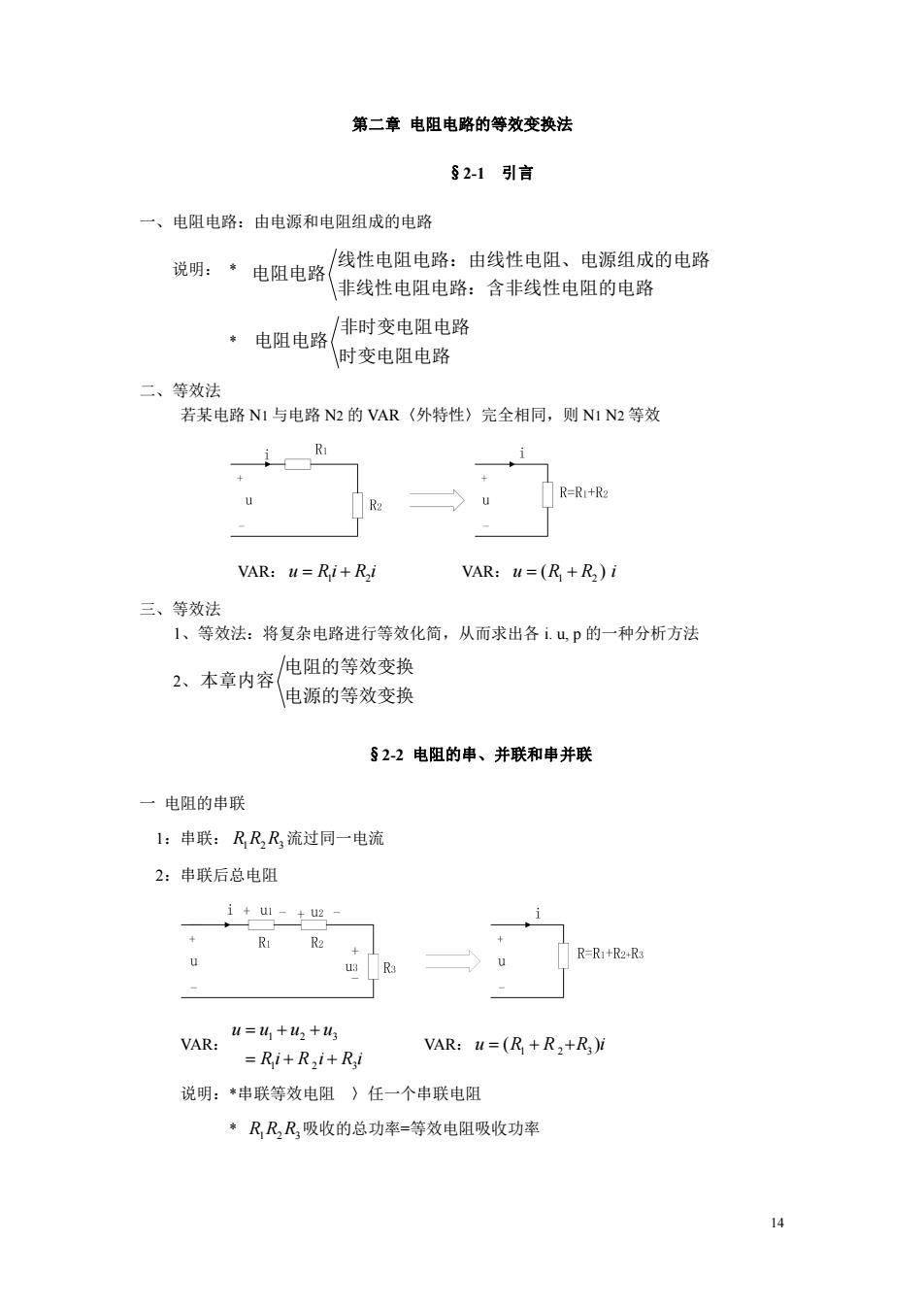
第二章电阻电路的等效变换法 §2-1引言 一、电阻电路:由电源和电阻组成的电路 说明:*电阻电路 线性电阻电路:由线性电阻、电源组成的电路 非线性电阻电路:含非线性电阻的电路 非时变电阻电路 电阻电路 时变电阻电路 二、等效法 若某电路NI与电路N2的VAR(外特性〉完全相同,则N1N2等效 R R=R1+R2 VAR:u=Ri+Ri VAR:u=(R+R,)i 三、等效法 1、等效法:将复杂电路进行等效化简,从而求出各i.u,p的一种分析方法 电阻的等效变换 2、本章内容 电源的等效变换 §2-2电阻的串、并联和串并联 一电阻的串联 1:串联:RR,R流过同一电流 2:串联后总电阻 1+u1-+u2 4 Ri R2 R-R1+R2+R3 13 R u=41+2+3 VAR: VAR:u=(R+R,+R)i =Ri+R,i+Ri 说明:*串联等效电阻〉任一个串联电阻 *RR,R吸收的总功率=等效电阻吸收功率 g
14 第二章 电阻电路的等效变换法 §2-1 引言 一、电阻电路:由电源和电阻组成的电路 说明: * * 非时变电阻电路 电阻电路 时变电阻电路 二、等效法 若某电路 N1 与电路 N2 的 VAR〈外特性〉完全相同,则 N1 N2 等效 VAR: 1 2 u R i R i VAR: 1 2 u (R R ) i 三、等效法 1、等效法:将复杂电路进行等效化简,从而求出各 i. u, p 的一种分析方法 2、 电阻的等效变换 本章内容 电源的等效变换 §2-2 电阻的串、并联和串并联 一 电阻的串联 1:串联: R1R2R3 流过同一电流 2:串联后总电阻 VAR: 1 2 3 1 2 3 u u u u R i R i R i VAR: 1 2 3 u (R R R )i 说明:*串联等效电阻 〉任一个串联电阻 * R1R2R3吸收的总功率=等效电阻吸收功率 线性电阻电路:由线性电阻、电源组成的电路 电阻电路 非线性电阻电路:含非线性电阻的电路
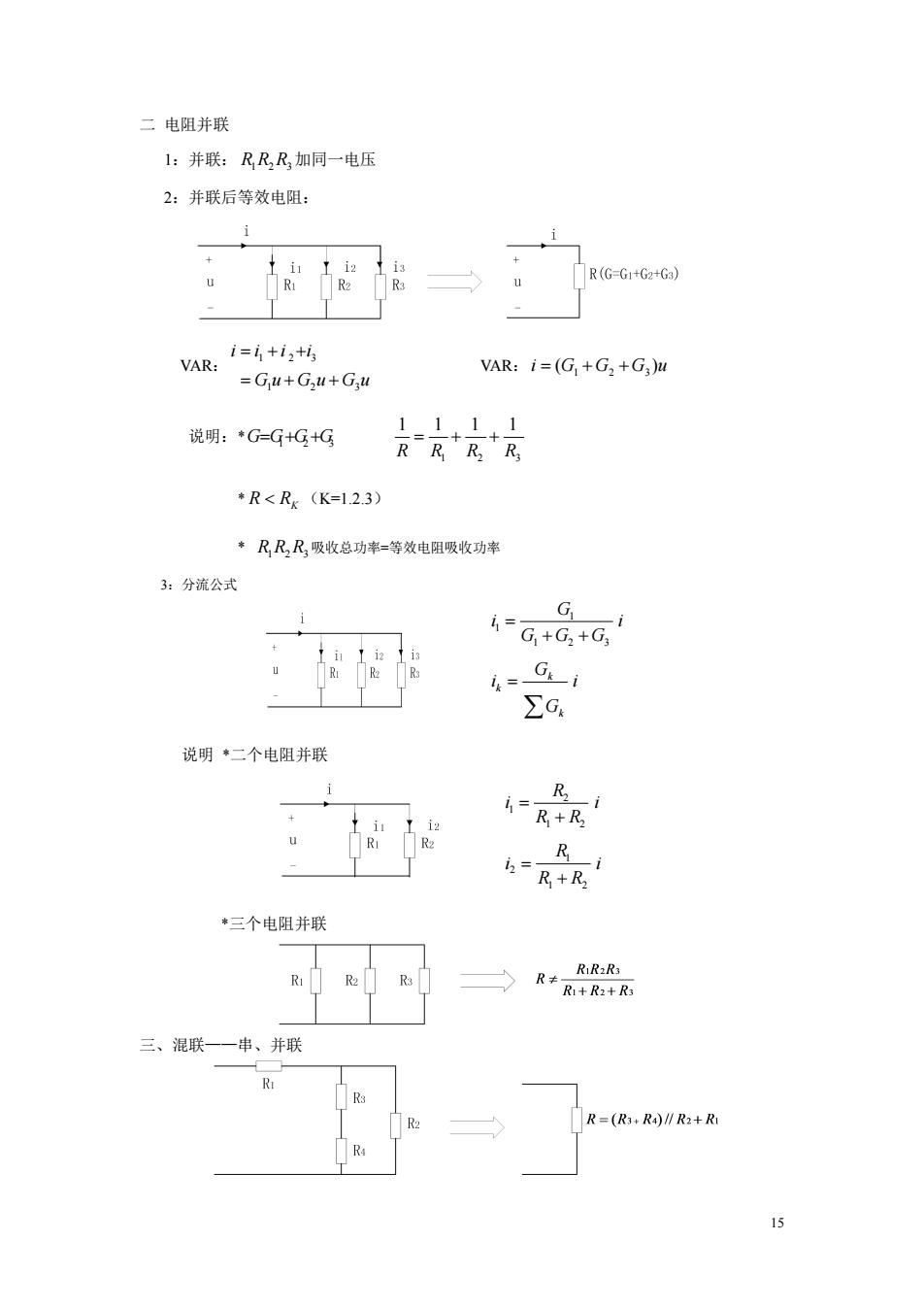
二电阻并联 1:并联:RRR加同一电压 2:并联后等效电阻: + 1i2 R(G-G1+G2+G3) u R2 R3 i=i+i+is VAR: VAR:i=(G +G2+G3)u =Gu+Gu+Gu 说明:*G=G+G+G 1=1+1+1 RRRR *R<Rx(K=1.2.3) *RR,R吸收总功率=等效电阻吸收功率 3:分流公式 G 1= i G+G,+G Rs i4= Gki ∑c. 说明*二个电阻并联 i + i=R+ u R2 iz=R+R *三个电阻并联 RiR2R3 R2 R3 R R1+R2+R3 三、混联一一串、并联 R3 R2 R=(R3+R4)∥R2+R1 15
15 二 电阻并联 1:并联: R1R2R3加同一电压 2:并联后等效电阻: VAR: 1 2 3 1 2 3 i i i i G u G u G u VAR: 1 2 3 i (G G G )u 说明:*GG1G2G3 1 2 3 1 1 1 1 R R R R * R RK (K=1.2.3) * R1R2R3 吸收总功率=等效电阻吸收功率 3:分流公式 说明 *二个电阻并联 *三个电阻并联 三、混联——串、并联 1 1 1 2 3 G i i G G G k k k G i i G 2 1 1 2 R i i R R 1 2 1 2 R i i R R