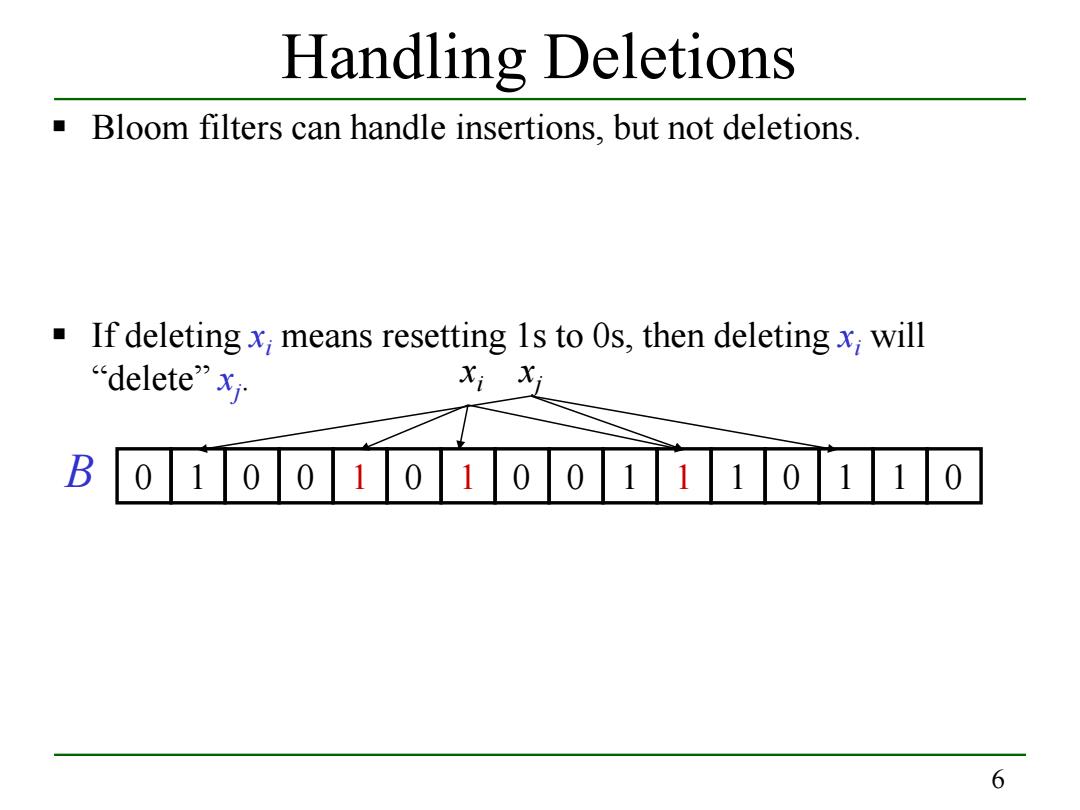
Handling Deletions Bloom filters can handle insertions,but not deletions. If deleting x;means resetting 1s to 0s,then deleting x;will delete”xy Xi Xi B 0100101001110110 6
6 Handling Deletions Bloom filters can handle insertions, but not deletions. If deleting xi means resetting 1s to 0s, then deleting xi will “delete” xj . B 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0 xi xj

Counting Bloom Filters Start with an m bit array,filled with 0s. B 000000000000 0 000 Hash each item x;in Sk times.If H(x)=a,add 1 to B[a]. B 0300102003210210 To delete x,decrement the corresponding counters. B 0200002003210110 Can obtain a corresponding Bloom filter by reducing to 0/1 B 0100001001110110 7
7 Counting Bloom Filters Start with an m bit array, filled with 0s. Hash each item xj in S k times. If Hi (xj ) = a, add 1 to B[a]. B 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B 0 3 0 0 1 0 2 0 0 3 2 1 0 2 1 0 To delete xj decrement the corresponding counters. B 0 2 0 0 0 0 2 0 0 3 2 1 0 1 1 0 Can obtain a corresponding Bloom filter by reducing to 0/1. B 0 1 0 0 0 0 1 0 0 1 1 1 0 1 1 0

Counting Bloom Filters:Overflow Must choose counters large enough to avoid overflow. Poisson approximation suggests 4 bits/counter. -Average load using k=(In 2)m/n counters is In 2. -Probability a counter has load at least 16: Failsafes possible. We assume 4 bits/counter for comparisons. ≈en2(In2)16/16l≈6.78E-17 8
8 Counting Bloom Filters: Overflow Must choose counters large enough to avoid overflow. Poisson approximation suggests 4 bits/counter. ─ Average load using k = (ln 2)m/n counters is ln 2. ─ Probability a counter has load at least 16: Failsafes possible. We assume 4 bits/counter for comparisons. (ln 2) /16! 6.78E 17 ln 2 16 ≈ ≈ − − e
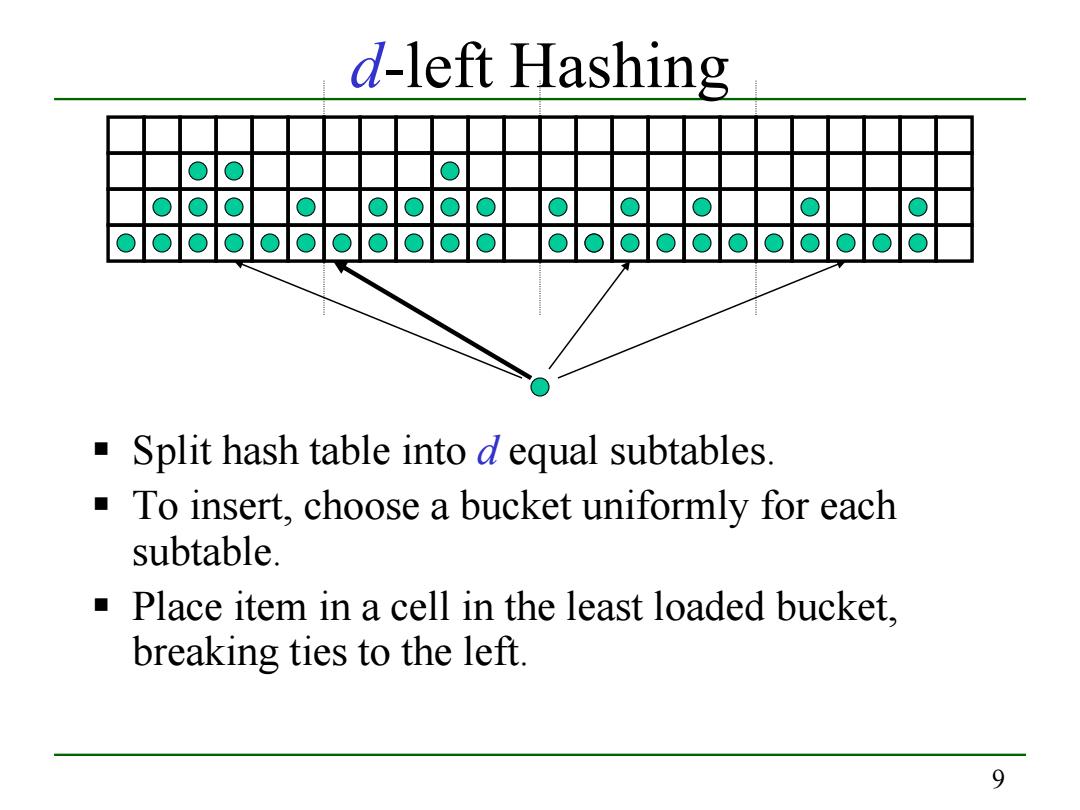
d-left Hashing ooooooooooo■ oooooooooo■ Split hash table into d equal subtables To insert,choose a bucket uniformly for each subtable. Place item in a cell in the least loaded bucket. breaking ties to the left. 9
9 d-left Hashing Split hash table into d equal subtables. To insert, choose a bucket uniformly for each subtable. Place item in a cell in the least loaded bucket, breaking ties to the left

Properties of d-left Hashing Analyzable using both combinatorial methods and differential equations. -Maximum load very small:O(log log n). -Differential equations give very,very accurate performance estimates. Maximum load is extremely close to average load for small values of d. Power of 2 choices! 10
10 Properties of d-left Hashing Analyzable using both combinatorial methods and differential equations. ─ Maximum load very small: O(log log n). ─ Differential equations give very, very accurate performance estimates. Maximum load is extremely close to average load for small values of d. Power of 2 choices!