
3、1 复数主值 =rei(p+2kz) (-π<p≤π,k为整数), 当k=0时,z=ep (-π<p≤r) 一复数主值 4、复数特例 当Rez=x=0时,复数z=x+退化为纯虚数;而当mz=Jy=0时, 复数退化为实数。 例求cos(a+ib) 的代数式 解:coa+0)-em+eo1=e+eo) -le(cs+isin)e(cosa-isina) ete-b eb-e-b =cosa 2 -isina 2 =cosa.chb-isina·shb
11 3、复数主值 ( 2 ) ( , ), i k z re k + = − 为整数 当k=0时, ( ). i z re = − 复数主值 4、复数特例 当Rez=x0时,复数z=x+iy退化为纯虚数;而当Imz=y0时, 复数退化为实数。 例 求 的代数式 解: cos( ) a ib + 1 1 ( ) ( ) cos( ) [ ] ( ) 2 2 1 = [ (cos sin ) (cos sin )] 2 = cos sin 2 2 = cos - sin i a ib i a ib b ia b ia b b b b b b a ib e e e e e a i a e a i a e e e e a i a a chb i a shb + − + − + − − − − + = + = + + + − + − −

二、复数的运算及其几何意义 1、加法和减法 1+z2=(x1+x2)+iy1+y2) 31+32 y 1 z1-z2=(x1-x2)+iy1-y2) y2 Z1-2 乙,和z2的加法为平行四边 法则得到的矢量+2·如 图(a) Xx2 (@ (b)
12 二、复数的运算及其几何意义 1、加法和减法 1 2 1 2 1 2 z z x x i y y + = + + + ( ) ( ) 1 2 1 2 1 2 z z x x i y y − = − + − ( ) ( ) z1和z2的加法为平行四边 法则得到的矢量z1+z2 . 如 图(a) x x 2 x 1 x 1 2 x x + 1 y 2 y y 1 z 2 z 1 2 z z + 2 x 1 x 1 y 2 y 2 z 1 z 1 2 z z − y ( ) a ( ) b

z1和z2的减法为三角形作图法得到的矢量z12,如图(b) z和☑2分别表示z和z2矢量的长度,亿+2小1-2分别代表矢 量+忆2、z2的模.根据三角形的两边之和大于(等于)第三 边,两边之差小于(等于)第三边: l31|-|z2ls31+z2sz1|+|z21 1一2 l3|-|z2lsz1-z2图31+|z21 从图(b)中,可以发现 (b) 131-z2曰2-1=√(x1-x2)2+(1-y2)2 k1z2或k2为平面上乙1、2两点的距离.因此,复平面上 满足-z1=k-2的z点轨迹是z1、z2两点连线的垂直平分线, 该直线上所有的点到z1、2两点的距离相等
13 z1和z2的减法为三角形作图法得到的矢量z1 -z2,如图(b). |z1 |和|z2 |分别表示z1和z2矢量的长度,|z1+z2 |、|z1 -z2 |分别代表矢 量z1+z2、z1 -z2的模. 根据三角形的两边之和大于(等于)第三 边,两边之差小于(等于)第三边: 1 2 1 2 1 2 || | | || | | | | | | z z z z z z − + + 1 2 1 2 1 2 || | | || | | | | | | z z z z z z − − + 从图(b)中,可以发现 2 2 1 2 2 1 1 2 1 2 | | | | ( ) ( ) z z z z x x y y − = − = − + − |z1 -z2 |或|z2 -z1 |为平面上z1、z2两点的距离. 因此,复平面上 满足|z-z1 |=|z-z2 |的z点轨迹是z1、z2两点连线的垂直平分线, 该直线上所有的点到z1、z2两点的距离相等
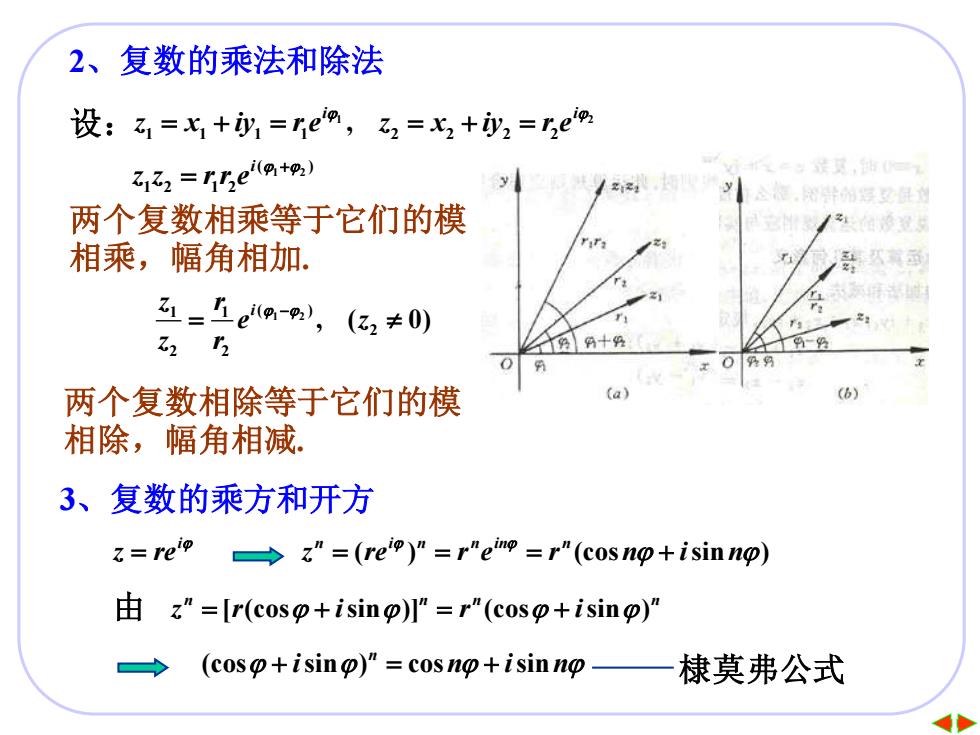
2、复数的乘法和除法 设:乙1=x+y=e9,乙2=x2+y2=2e0 名32=r5eat9) /, 公他,用导州导父且的 两个复数相乘等于它们的模 相乘,幅角相加: 1=上ep),(亿2≠0) Z22 0 两个复数相除等于它们的模 (6) 相除,幅角相减。 3、复数的乘方和开方 t=rep →z"=(re9)”=r"emp=r"(cos np+isinng) 由z"=[r(cosp+ising)"=r"(cosp+ising)” (coso+ising)"=cosno+isinno 棣莫弗公式
14 2、复数的乘法和除法 设: 1 2 1 1 1 1 2 2 2 2 , i i z x iy r e z x iy r e = + = = + = 1 2 ( ) 1 2 1 2 i z z r r e + = 两个复数相乘等于它们的模 相乘,幅角相加. 1 2 1 1 ( ) 2 2 2 , ( 0) z r i e z z r − = 两个复数相除等于它们的模 相除,幅角相减. 3、复数的乘方和开方 i z re = ( ) (cos sin ) n i n n in n z re r e r n i n = = = + 由 [ (cos sin )] (cos sin ) n n n n z r i r i = + = + (cos sin ) cos sin n + = + i n i n 棣莫弗公式

开方:7=ep+2 )(k=0,1,2,. E=eea=7e2gk=0,12,0m-1) 可见一个复数开n次方应有n个值复数开方的多值性显然是 由于复数幅角可相差2π的整数倍引起的.实际上,复数的乘 方和开方并不仅仅限于为自然数,n完全可以是复数,如Vi 或等等,并且它们都有无穷多个值 例如: (匹+2ki=p(2+2kπ) Vi-e (k=0,±1,±2,.) +2kπ)i-(+2kπ) i=e 三e (k=0,±1,±2,.)
15 开方: i k ( 2 ) z re + = ( 0, 1, 2, ) k = 2 ( 2 ) 1/ [ ] k i n n i k n n z re re + + = = k n = − 0,1,2, ,( 1) 可见一个复数开n次方应有n个值复数开方的多值性显然是 由于复数幅角可相差2 的整数倍引起的.实际上,复数的乘 方和开方并不仅仅限于n为自然数,n完全可以是复数,如 或 等等,并且它们都有无穷多个值. i i i i 例如: ( 1 ( 2 ) 2 ) 2 2 ( 2 ) ( 2 ) 2 2 ( 0, 1, 2, ) ( 0, 1, 2, ) i k k i i i k i k i i e e k i e e k + + + − + = = = = = =