
历安毛子代枚大学 (1)GraphSAGE XIDIAN UNIVERSITY 整合函数(卷积操作)。有三种整合函数(图中的整合加拼接), (1)平均整合: CONCAT(1,hvi)=mean(hh,VvjE N(vi)), (6-1) 式(6-1)的操作可以理解为卷积,卷积的结果就是将节点x及其邻居在上一步 的表示进行平均: (2)LSTM aggregator; (3)Pooling aggregator:池化整合是一种对称可训练的整合方法,每个邻居节 点的表达矢量独立通过一个神经网络,最大池化操作以整合邻居节点信息。 Wpoot?是神经网络参数。 AGGREGATEROOL max({(WpooLh1),Vvj E N(vi)}). (6-2) 7
(1) GraphSAGE 7 • 整合函数(卷积操作)。有三种整合函数(图中的整合加拼接), (1)平均整合: CONCAT ℎ𝑣𝑖 𝑘−1 , ℎ𝑁(𝑣𝑖) 𝑘 = 𝑚𝑒𝑎𝑛 ℎ𝑣𝑖 𝑘−1 ∪ ℎ𝑣𝑗 𝑘−1 , ∀𝑣𝑗 ∈ 𝑁(𝑣𝑖) , (6-1) 式(6-1)的操作可以理解为卷积,卷积的结果就是将节点xi及其邻居在上一步 的表示进行平均; (2)LSTM aggregator; (3)Pooling aggregator: 池化整合是一种对称可训练的整合方法,每个邻居节 点的表达矢量独立通过一个神经网络,最大池化操作以整合邻居节点信息。 𝑊𝑝𝑜𝑜𝑙是神经网络参数。 AGGREGATE𝑘 𝑝𝑜𝑜𝑙 = max {σ(𝑊𝑝𝑜𝑜𝑙ℎ𝑣𝑗 𝑘−1 ), ∀𝑣𝑗 ∈ 𝑁 𝑣𝑖 } , (6-2)

历柴毛子代枝大学 (1)GraphSAGE XIDIAN UNIVERSITY 关于邻居节点抽样。在图6-5的节点嵌入表达矢量生成的算法中,为了减少 计算复杂性,一个节点的邻居节点并不是它所有的邻居节点,而是进行均匀 随机抽样。限定邻居节点集合的大小,从实际邻居节点集中随机均匀抽样固 定大小的邻居节点构成邻居集合(),y,∈V。限定邻居集合大小以后,算 法的复杂性变为0(Π1S),从实验结果来说,K=2就能取得较好的性能, 且S1S2≤500。 8
(1) GraphSAGE 8 • 关于邻居节点抽样。在图6-5的节点嵌入表达矢量生成的算法中,为了减少 计算复杂性,一个节点的邻居节点并不是它所有的邻居节点,而是进行均匀 随机抽样。限定邻居节点集合的大小,从实际邻居节点集中随机均匀抽样固 定大小的邻居节点构成邻居集合N(vi ),vi∈V。限定邻居集合大小以后,算 法的复杂性变为O 𝑆𝑖 𝐾 𝑖=1 , 从实验结果来说,K=2就能取得较好的性能, 且S1·S2≤500

历些毛子代枝大学 (1)GraphSAGE XIDIAN UNIVERSITY 参数的学习 用随机梯度下降法,采用一个基于图的损失函数来调整权矩阵W Vk∈{1,.,K,以及整合函数中的参数。基于图的损失函数应使相连的节点 有相似的表示,远离的节点有不相似的表示。采用对数损失函数: Jg(zvi)=-log(a(zvizvj)-Q.Evn-Plog(-a(zvzun)),(6-2) ·式中,y,是一个在节点v,附近固定的随机游走长度内出现的节点,o是sigmoid 函数,P是负抽样的分布,Q是负抽样的个数。需要说明的是,这里反馈到 损失函数的节点的表示z,是通过节点及近邻的特征产生的,而不是训练得到 的节点的嵌入表示。 9
(1) GraphSAGE 9 2 参数的学习 • 用随机梯度下降法,采用一个基于图的损失函数来调整权矩阵Wk , ∀k∈{1,…,K}, 以及整合函数中的参数。基于图的损失函数应使相连的节点 有相似的表示,远离的节点有不相似的表示。采用对数损失函数: 𝐽𝑔 𝑧𝑣𝑖 = − log 𝜎 𝑧𝑣𝑖 𝑇 𝑧𝑣𝑗 − 𝑄 ∙ E𝑣𝑛~𝑃𝑛 log(−𝜎 𝑧𝑣𝑖 𝑇 𝑧𝑣𝑛 ), (6-2) • 式中,vj是一个在节点vi附近固定的随机游走长度内出现的节点,σ是sigmoid 函数,Pn是负抽样的分布,Q是负抽样的个数。需要说明的是,这里反馈到 损失函数的节点的表示zvi是通过节点及近邻的特征产生的,而不是训练得到 的节点的嵌入表示
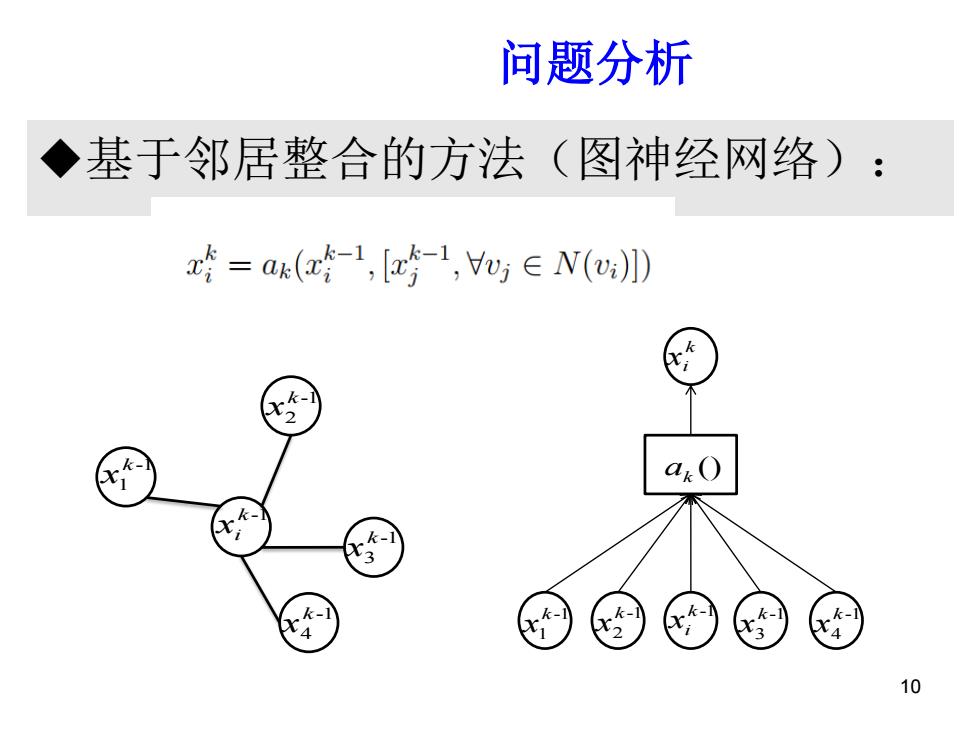
问题分析 ◆基于邻居整合的方法 (图神经网络): x=ax(a-1,[z-1,y∈V(》 k k-1 10
基于邻居整合的方法(图神经网络): 问题分析背景 10 k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x () ak k xi k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x
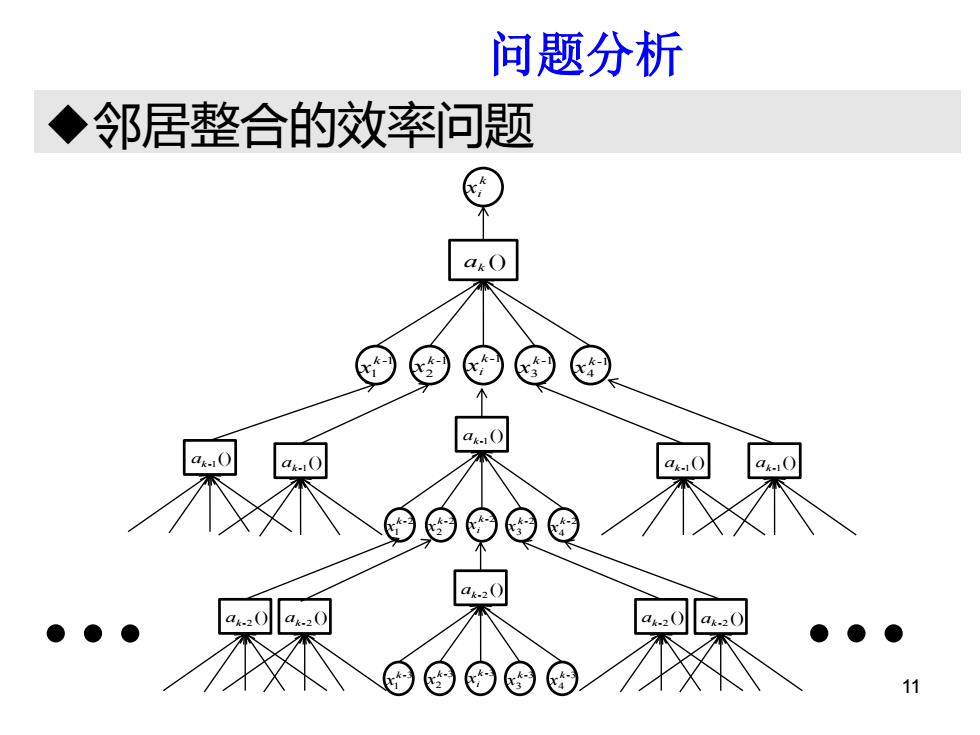
问题分析 ◆邻居整合的效率问题 a.0 a.0 11
邻居整合的效率问题 研问题分析究背景 11 () ak k xi k -1 xi -1 1 k x -1 2 k x -1 3 k x -1 4 k x () ak-1 k -2 xi -2 1 k x -2 2 k x -2 3 k x -2 4 k x () ak-1 () ak-1 () ak-1 () ak-1 () ak-2 k -3 xi -3 1 k x -3 2 k x -3 3 k x -3 4 k x () ak-2 () ak-2 () ak-2 () ak-2