
第2章(上):填值函数—亦或不是? 现在的麻烦是,把两个明显有效的推断串连在一起,我们会得到明显无效的 推断,像这样: 女王富有。 女王富有或猪会飞。女王不富有。 猪企飞 这不可能是对的。将两个有效的推断以这种方式连接起来不可能得到一个无 效的推断。(译者注:对于有效的论证)任何情形下如果所有前提为填,那 么它们的所有结论也为其,由这些结论推得的结论也为其,如此下去,直到 我们得到最终的结论。问题出在哪儿呢? 为了给这个问题一个正统的解答,让我们更详细地考察一下。首先·我们把 语句“猪会飞”记作p,把语句“女王富有”记作q’这让事情更紧凑些,但不止 于此:如果你思考一下就会发现,在这个例子中使用什么具体语句是无关紧 要的·我完全可以使用任意两个语句来构造这种形式的推断,因此我们可以 忽略其内容,这正是我们将语句记作单个字母时所做的· 语句“女王富有或猪会飞”现在就变成“q或p”,逻辑学家通常将其记作 qVp。“女王不富有”怎么记呢?让我们先把这句话改写为“并非女王富有”,将 否定词挪到句子前面。这样,这句话就变成“并非g”,逻辑学家通常将其记作 g,称为g的否定(negation)。“女王富有且猪会飞”,也就是“g且p”这句 话怎么记呢?适辑学家通常将其记作g八p,称为g和p的合取 (conjunction)。有了这套改写机制,我们就可以把上面那个串连起来的推断 写成如下形式: qVPq p 关于这个推断我们有什么要说的呢? 语句可以为其,可也以为假。让我们用T表示其,用F表示假。自现代逻辑 的莫基者之一,德国哲学家和数学家弗雷格之后,它们通常被称为真值 (truth values)。给定任何语句a'a的填值与其否定a的填值之间有何联
现在的麻烦是,把两个明显有效的推断串连在一起,我们会得到明显无效的 推断,像这样: 女王富有。 —————————————— 女王富有或猪会飞。 女王不富有。 ———————————————————————— 猪会飞 这不可能是对的。将两个有效的推断以这种方式连接起来不可能得到一个无 效的推断。(译者注:对于有效的论证)任何情形下如果所有前提为真,那 么它们的所有结论也为真,由这些结论推得的结论也为真,如此下去,直到 我们得到最终的结论。问题出在哪儿呢? 为了给这个问题一个正统的解答,让我们更详细地考察一下。首先,我们把 语句“猪会飞”记作 p,把语句“女王富有”记作 q,这让事情更紧凑些,但不止 于此:如果你思考一下就会发现,在这个例子中使用什么具体语句是无关紧 要的,我完全可以使用任意两个语句来构造这种形式的推断,因此我们可以 忽略其内容,这正是我们将语句记作单个字母时所做的。 语句“女王富有或猪会飞”现在就变成“ q 或 p ”,逻辑学家通常将其记作 q ∨ p。“女王不富有”怎么记呢?让我们先把这句话改写为“并非女王富有”,将 否定词挪到句子前面。这样,这句话就变成“并非 q”,逻辑学家通常将其记作 ¬q,称为 q 的否定(negation)。“女王富有且猪会飞”,也就是“ q 且 p ”这句 话怎么记呢?逻辑学家通常将其记作 q ∧ p,称为 q 和 p 的合取 (conjunction)。有了这套改写机制,我们就可以把上面那个串连起来的推断 写成如下形式: 关于这个推断我们有什么要说的呢? 语句可以为真,可也以为假。让我们用 T 表示真,用 F 表示假。自现代逻辑 的奠基者之一,德国哲学家和数学家弗雷格之后,它们通常被称为真值 (truth values)。给定任何语句 a,a 的真值与其否定 ¬a 的真值之间有何联 p q ∨ p ¬q q 第2章(上):真值函数——亦或不是? 11
第2章(上):其值函数一亦或不是? 系呢?一个自然的回答是,如果一个为其,另一个就为假,反之亦然。这 样,如果“女王富有”为填,则“女王不富有”就为假,反之亦然·我们可以将这 一联系记录如下: ·a具有旗值T,当且仅当a具有旗值F。 ·a具有其值F,当且仅当a具有其值T。 逻辑学家将其称为否定的其值条件(truth conditions)。如果我们假定每个语 句或者为填或者为假,但不会既真又假,我们就可以用下面的表格来描绘这 些条件,辽辑学家称之为填值表(truth table): a a T F T 如果a具有它下面那一列的真值,a就具有其右边对应的的其值。析取V的 填值条件呢?正如我已提到的,一个自然的假设是,一个析取式aVb为填, 若a和b中的其中一个(或两个都)为其,否则该析取式就为假。我们可以 将这一联系记录在析取的其值条件中: ·aVb具有其值T,当且仅当a和b中至少有一个具有其值T。 ·aVb具有旗值F,当且仅当a和b都具有填值F。 这些条件可以用填值表描绘如下: a b avb T T T T F T F F 除了第1行的表头,每一行记录了一种a(第1列)与b(第2列)的填值 的可能组合。共有4种这样可能的组合,因而有4行。对每一种组合,右边 都给出了aVb对应的莫值(第3列)。 12
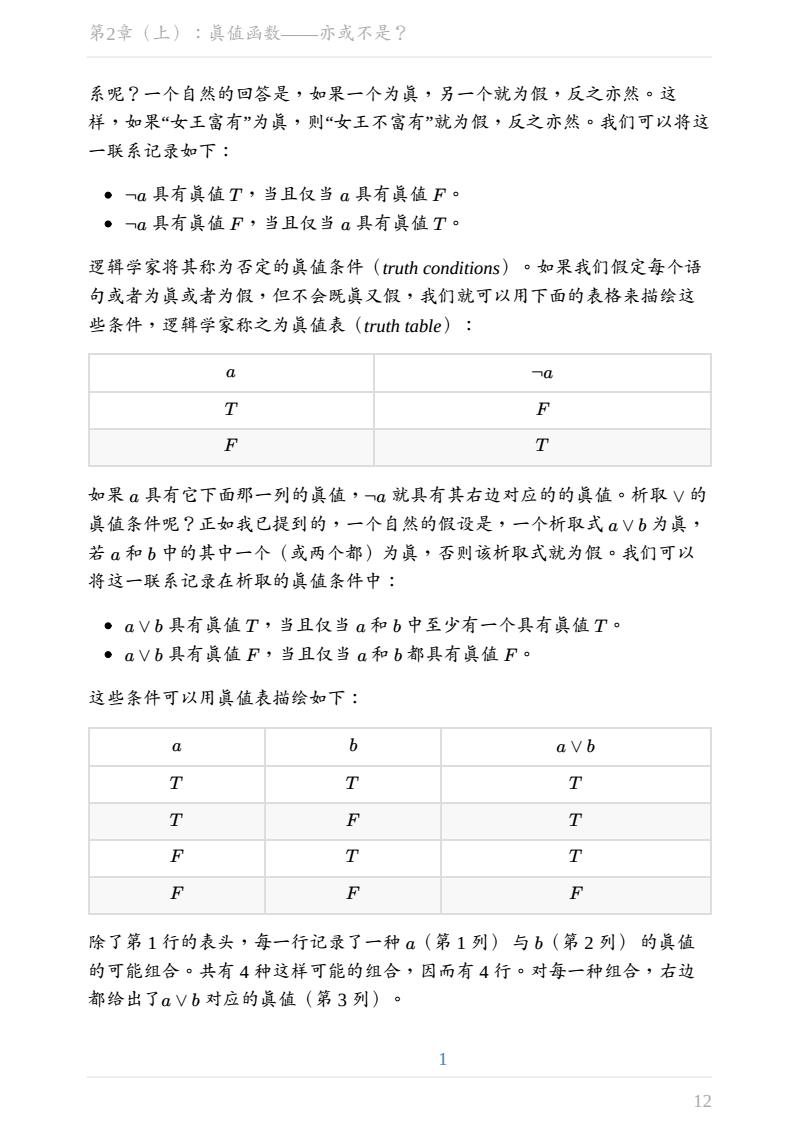
系呢?一个自然的回答是,如果一个为真,另一个就为假,反之亦然。这 样,如果“女王富有”为真,则“女王不富有”就为假,反之亦然。我们可以将这 一联系记录如下: ¬a 具有真值 T,当且仅当 a 具有真值 F。 ¬a 具有真值 F,当且仅当 a 具有真值 T。 逻辑学家将其称为否定的真值条件(truth conditions)。如果我们假定每个语 句或者为真或者为假,但不会既真又假,我们就可以用下面的表格来描绘这 些条件,逻辑学家称之为真值表(truth table): a ¬a T F F T 如果 a 具有它下面那一列的真值,¬a 就具有其右边对应的的真值。析取 ∨ 的 真值条件呢?正如我已提到的,一个自然的假设是,一个析取式 a ∨ b 为真, 若 a 和 b 中的其中一个(或两个都)为真,否则该析取式就为假。我们可以 将这一联系记录在析取的真值条件中: a ∨ b 具有真值 T,当且仅当 a 和 b 中至少有一个具有真值 T。 a ∨ b 具有真值 F,当且仅当 a 和 b 都具有真值 F。 这些条件可以用真值表描绘如下: a b a ∨ b T T T T F T F T T F F F 除了第 1 行的表头,每一行记录了一种 a(第 1 列) 与 b(第 2 列) 的真值 的可能组合。共有 4 种这样可能的组合,因而有 4 行。对每一种组合,右边 都给出了a ∨ b 对应的真值(第 3 列)。 1 第2章(上):真值函数——亦或不是? 12

第2章(上):填值函数—亦或不是? 同样,既然谈到这里,a和b的真值与a八b的英值之问有何联系呢?一个自 然的假定是,a八b为填,若a和b都为填,否则aΛb为假。这样,比 如,“约翰35岁且有棕色的头发”为其,当且仅当“约翰35岁”和“约翰有棕色 的头发”都为員。我们可以将这一联系记录在合取的真值条件中: ·aΛb具有其值T,当且仅当a和b都具有真值T。 ·a八b具有旗值F,当且仅当a和b中至少有一个具有旗值F。 这些条件可以用填值表描绘如下: a b anb T 2 T F F F F F 1,译者注:原文对合取采用的记号是&,中译采用了更标准的记号A。 13
同样,既然谈到这里,a 和 b 的真值与 a ∧ b 的真值之间有何联系呢?一个自 然的假定是,a ∧ b 为真,若 a 和 b 都为真,否则 a ∧ b 为假。这样,比 如,“约翰 35 岁且有棕色的头发”为真,当且仅当“约翰 35 岁”和“约翰有棕色 的头发”都为真。我们可以将这一联系记录在合取的真值条件中: a ∧ b 具有真值 T,当且仅当 a 和 b 都具有真值 T。 a ∧ b 具有真值 F,当且仅当 a 和 b 中至少有一个具有真值 F。 这些条件可以用真值表描绘如下: a b a ∧ b T T T T F F F T F F F F . 译者注:原文对合取采用的记号是 &,中译采用了更标准的记号 ∧。 ↩ 1 1 第2章(上):真值函数——亦或不是? 13

第2章(下)其值函数—亦或不是? 第2章(下):真值函数一亦或不 是? 那么,所有这些与我们一开始提出的问题有何关系呢?让我们回到我在上一 章结束时提出的问题:什么是一个情形?一个自然的想法是,不管情形是什 么,它确定了每个语句的其值。因此,比如,在某个特定情形中,女王富有 为填而猪会飞为假。在另一个情形中,女王富有为假而猪会飞为旗。(注意 这些情形可以纯粹是假设性的!)换言之,一个情形确定了每个相关语句为 其或为假。这里的相关语句不包含“且”、“或”或“非”的任何出现。给定关于某 个情形的基本信息·包含这些词的语句的填值我们可以利用填值表算出· 例如,假设我们有下面的情形: p:T q:F r:T (r可能是语句“大黄有营养”,“p:T”表示p被指派填值T,等等。)那么, 比方说pA(TVg)的旗值是多少呢?我们计算这一填值的方法,和用乘法表 与加法表计算3×(-6+2)的数值完全一样。于是,一的填值表告诉我们· r的填值是F。又由于q的其值也是F,V的真值表告诉我们,rVg的填 值为F。由于p的填值是T(译者注:这里其实不需要考虑这一条件)·人 的填值表告诉我们·pA(一TVg)的填值为F。用这种逐步计算的方法,我们 可以算出任何包含A,V和一出现的公式的真位· 现在,回想一下,上一章我们说一个推断是有效的,只要不存在使得所有前 提都为填而结论不为填(为假)的情形。也就是说,一个推断是有效的,只 要不存在对相关语句的填值指派,使得所有前提的其值都为T而结论的填值 为F。比如,考虑我们前面见过的推断:q/gVp。(我把它写成一行是为了 给牛津大学出版社省点钱。)这里的相关语句是q和p。有4种真值组合,对 每种组合我们都能算出前提和结论的其值。我们可以将结果表示如下: 14
第 2 章(下):真值函数——亦或不 是? 那么,所有这些与我们一开始提出的问题有何关系呢?让我们回到我在上一 章结束时提出的问题:什么是一个情形?一个自然的想法是,不管情形是什 么,它确定了每个语句的真值。因此,比如,在某个特定情形中,女王富有 为真而猪会飞为假。在另一个情形中,女王富有为假而猪会飞为真。(注意 这些情形可以纯粹是假设性的!)换言之,一个情形确定了每个相关语句为 真或为假。这里的相关语句不包含“且”、“或”或“非”的任何出现。给定关于某 个情形的基本信息,包含这些词的语句的真值我们可以利用真值表算出。 例如,假设我们有下面的情形: p : T q : F r : T (r 可能是语句“大黄有营养”,“p : T”表示 p 被指派真值 T,等等。)那么, 比方说 p ∧ (¬r ∨ q) 的真值是多少呢?我们计算这一真值的方法,和用乘法表 与加法表计算 3 × (−6 + 2) 的数值完全一样。于是, ¬ 的真值表告诉我们, ¬r 的真值是 F。又由于 q 的真值也是 F,∨ 的真值表告诉我们,¬r ∨ q 的真 值为 F。由于 p 的真值是 T(译者注:这里其实不需要考虑这一条件),∧ 的真值表告诉我们,p ∧ (¬r ∨ q) 的真值为 F。用这种逐步计算的方法,我们 可以算出任何包含 ∧,∨ 和 ¬ 出现的公式的真值。 现在,回想一下,上一章我们说一个推断是有效的,只要不存在使得所有前 提都为真而结论不为真(为假)的情形。也就是说,一个推断是有效的,只 要不存在对相关语句的真值指派,使得所有前提的真值都为 T 而结论的真值 为 F。比如,考虑我们前面见过的推断:q/q ∨ p。(我把它写成一行是为了 给牛津大学出版社省点钱。)这里的相关语句是 q 和 p。有 4 种真值组合,对 每种组合我们都能算出前提和结论的真值。我们可以将结果表示如下: 第2章(下)真值函数——亦或不是? 14
第2章(下)旗值函数—亦或不是? D q qVp T T T T T F T T F T 前两列给出了q和p的填位的所有可能组合·后两列分别给出了前提和结论 在每种组合下对应的填值。第3列与第1列相同,这是本例的一个巧合,之 所以如此是因为,在这个特定的例子中,前提恰好是其中一个相关语句。第4 列可以由析取的員值表读出·给定这些信息,我们就能看出这个推断是有效 的,因为没有一行前提q为填而结论qVp不为填。 推断qVp,qp的有效性如何呢?用同样的方法,我们得到: qvp g 3 T T T F T T F F T 2 2 F T F 这次有5列,因为有两个前提。前提和结论的填值可以由析取和否定的填值 表读出。同样,没有一行两个前提都为其而结论不为真。因此,该推断是有 效的。 我们一开始提到的那个推断q,g/p的有效性如何呢?用之前的方法,我们得 到: 9 D T T F T F T T 15
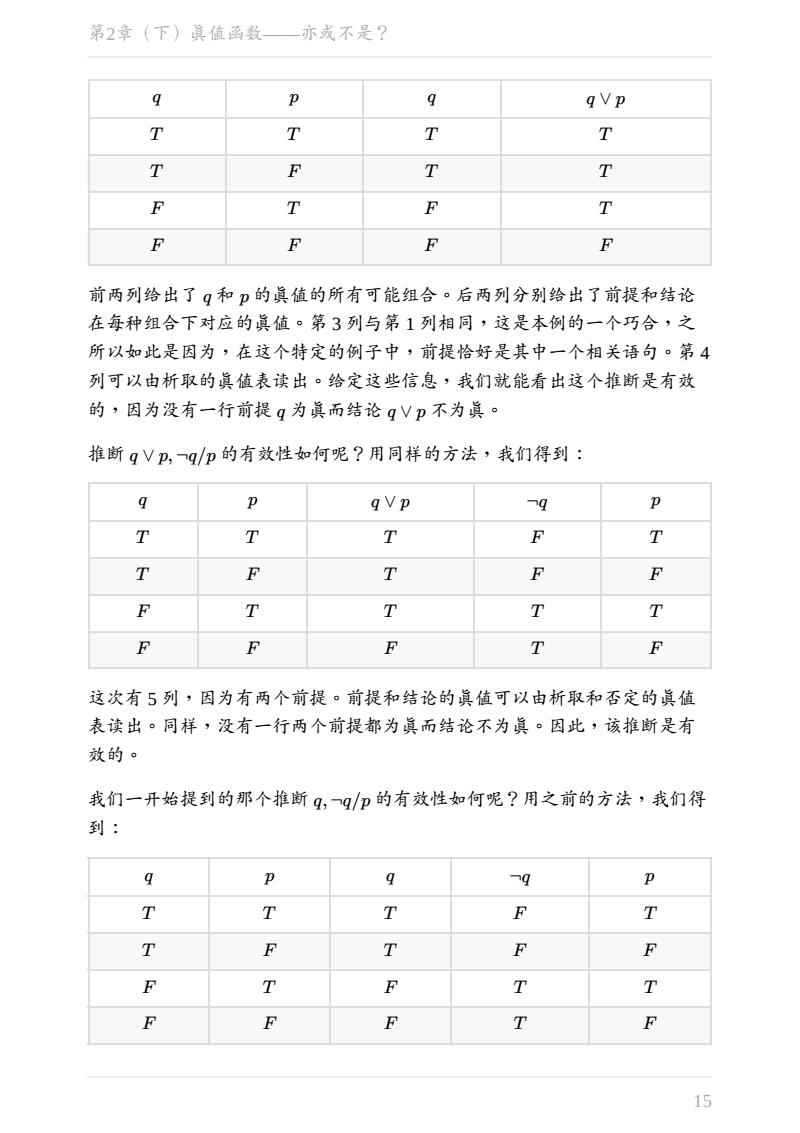
q p q q ∨ p T T T T T F T T F T F T F F F F 前两列给出了 q 和 p 的真值的所有可能组合。后两列分别给出了前提和结论 在每种组合下对应的真值。第 3 列与第 1 列相同,这是本例的一个巧合,之 所以如此是因为,在这个特定的例子中,前提恰好是其中一个相关语句。第 4 列可以由析取的真值表读出。给定这些信息,我们就能看出这个推断是有效 的,因为没有一行前提 q 为真而结论 q ∨ p 不为真。 推断 q ∨ p,¬q/p 的有效性如何呢?用同样的方法,我们得到: q p q ∨ p ¬q p T T T F T T F T F F F T T T T F F F T F 这次有 5 列,因为有两个前提。前提和结论的真值可以由析取和否定的真值 表读出。同样,没有一行两个前提都为真而结论不为真。因此,该推断是有 效的。 我们一开始提到的那个推断 q,¬q/p 的有效性如何呢?用之前的方法,我们得 到: q p q ¬q p T T T F T T F T F F F T F T T F F F T F 第2章(下)真值函数——亦或不是? 15